
题目列表(包括答案和解析)
7. 在△ABC中,若∠C= 90°,AC=1,BC=2,则下列结论中正确的是[ ]
(A)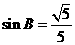 (B)
(B)  (C)
(C)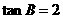 (D)
(D)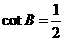
6.已知点P(m,-n)和点Q(-m,n),那么点P和点Q [ ]
(A)关于x轴对称 (B)关于y轴对称
(C)关于原点对称 (D)以上结论都不对
5. 已知:一个正多边形的每一个内角都等于120°,则这个多边形是[ ]
(A)正八边形 (B)正六边形 (C)正五边形 (D)正方形
4. 光年是天文学中的距离单位,1光年约是9500000000000km,用科学计数法表示为[ ]
(A)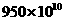 km (B)
km (B)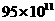 km (C)
km (C) km (D)
km (D) km
km
3. 如果内切两圆的半径分别为4cm和6cm , 则两圆的圆心距为 [ ]
(A)2cm (B) 5cm (C)10cm (D)20cm
2. 9的算术平方根是 [ ]
 (A)±3 (B)
(A)±3 (B)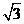 (C)3 (D)-3
(C)3 (D)-3
1. 计算-1-(-5)的结果是[ ]
(A)-6 (B)4 (C) 6 (D)-4
31.(本小题12分)
如图,梯形OABC中,BC∥AO,∠BAO=90°,B(-3 ,3),直线OC的解析式为
,3),直线OC的解析式为
y=- x,将ΔOBC绕点C顺时针旋转60°后,O到O1,B到B1,得ΔO1B1C.
x,将ΔOBC绕点C顺时针旋转60°后,O到O1,B到B1,得ΔO1B1C.
(1)求证:点O1在x轴上;
(2)将点O1运动到点M(-4 ,0),求∠B1MC的度数;
,0),求∠B1MC的度数;
(3)在(2)的条件下,将直线MC向下平移m个单位长度,设直线MC与线段AB交于点P,与线段OC的交于点Q,四边形OAPQ的面积为S,求S与m的函数关系式,并求出m的取值范围.

解:(1)由题意:C(- ,3)
,3)
∴tan∠COA=
∴∠COA=60°
∵∠OCO1=60°,CO=CO1
∴ΔCOO1为等边三角形
∴∠COO1=60°
∴∠COA=∠COO1
∴点O1在x轴上. ……4’
∵∠COO1=60°,BC∥AO
(2)∠BCO=120°
∴BCO1=120°
∵∠O1CO=60°
∴∠BCO=180°
∴B、C、O三点共线
∴C(- ,3)
,3)
∴CO=CO1=O1O=2
∵M1O=4
∴M1O1=O1O=O1C
可证得 ∠M1CO=90°
∵BC=CO=2
BC=B1C
∴B1C=CO
∴M1B=M1O
∴∠BM1C= ∠B1M1O=30° ……8’
∠B1M1O=30° ……8’
(2) ∵AD=1,PD=m
∴AP=1-m
在ΔCEQ中,CE=m,∠ECQ=30°
∴CQ= m
m
∴OQ=2 -
- m
m
∴QN=3- m,ON=
m,ON= -
- m
m
∴AN=2 +
+ m
m
又∵S四边形OAPQ=S梯形PAQN+SΔQNO
∴S= [(1―m)+(3―
[(1―m)+(3― m)][2
m)][2 +
+ m]+
m]+ (
( ―
― m)(3―
m)(3― m)
m)
∴S=― m2―2
m2―2 m+
m+
 (0<m<1) ……12’
(0<m<1) ……12’
28.(1)B(6,0)………………………………4分
(2) ………………………………8分
………………………………8分
(3)存在。N(-3,0)………………………………12分
24.解. (1)OA=OB,DF=EF,DE=AC,AG=DG,EG=CG. ………………………………3分
(2)ME=GM. 理由是:连EO并延长交⊙O于点N,连结DN.
∵EM是⊙O的切线,
∴∠OEM=90º,∴∠GEM+∠GEN=90º. …………………………………………5分
∵EN是⊙O的直径,∠N+∠GEN=90º,
∴∠N=∠GEM. ………………………………………………………………7分
∵AB是⊙O的直径,∴∠B+∠BAC=90º,
∵∠AGF+∠GAF=90º,∴∠AGF=∠B,……………………………………9分
∵∠AGF=∠CGE,∴∠CGE=∠B.
∵AC=DE,∴∠N=∠B,
∴∠GEM=∠CGE,∴MG=ME. ………………………………………………11分
(3)答案: .…………………………………………………………………14分
.…………………………………………………………………14分
28(本题满分12分)
如图:矩形的顶点在坐标原点O,OA在y轴上,A点坐标为(0,3),另一边OB在x的正半轴上,点M是AC边的中点,点P是OB边上一动点,PF⊥OM,PE⊥BM,垂足分别为E、F.
(1)若四边形PEMF为矩形,求B点坐标;
(2)在(1)的条件下,求过A、M、B三点的抛物线解析式;
(3)在抛物线上是否存在一点N,使得四边形AMON是平行四边形,若存在,求出点N的坐标,若不存在,说明理由。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com