
题目列表(包括答案和解析)
28、解:(1) ,
, ,
,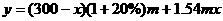
(2)由题意得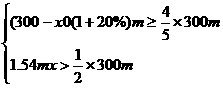
解得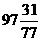 <
<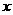 ≤100。注:写97.5<
≤100。注:写97.5<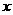 ≤100或97.4<
≤100或97.4<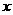 ≤100均视为正确
≤100均视为正确
∵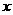 为整数 ∴
为整数 ∴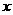 只能取98、99、100。
只能取98、99、100。
故共有三种调配方案:
①202人继续生产A种产品,调98人生产B种产品;
②201人继续生产A种产品,调99人生产B种产品;
③200人继续生产A种产品,调100人生产B种产品;
又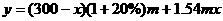 =
=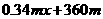 ,由于
,由于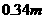 >0,函数
>0,函数 随
随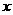 的增大而增大。故当
的增大而增大。故当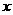 =100,即按第三种方案安排生产时,获总利润最大。
=100,即按第三种方案安排生产时,获总利润最大。
(3)当 =2时,最大总利润为788万元。根据题意,可投资开发产品F、H或C、D、E或C、D、G或C、F、G。
=2时,最大总利润为788万元。根据题意,可投资开发产品F、H或C、D、E或C、D、G或C、F、G。
(1)分别求点E, C的坐标.
(2)求经过A、C两点,且以过E而平行于y轴的直线为对称轴的抛物线的函数解析式.
 (3)设抛物线的对称轴与AC的交点为M,试判断以M点为圆心, ME为半径的圆与☉A的位置关系,并说明理由.
(3)设抛物线的对称轴与AC的交点为M,试判断以M点为圆心, ME为半径的圆与☉A的位置关系,并说明理由.
一个圆柱的一条母线为AB,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的表面爬行到点C.
⑴如图①,如果底面周长为24cm,高为4cm,那么蚂蚁的最短行程是多少cm?
⑵如图②,如果底面半径为rcm,高为hcm,那么你认为蚂蚁可能有哪几种行程较短的路径?试画出平面展开图说明路径(至少画两种不同的路径),不必说明理由.
⑶通过计算比较②中各种路径的长度,你能得到什么一般性的结论?或者说,蚂蚁选择哪条路径可使行程最短?

28、(12分)某企业有员工300人,生产A种产品,平均每人每年可创造利润 万元(
万元( 为大于零的常数)。为减员增效,决定从中调配
为大于零的常数)。为减员增效,决定从中调配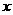 人去生产新开发的B种产品,根据评估,调配后,继续生产A种产品的员工平均每人每年创造的利润可增加20%,生产B种产品的员工平均每人每年可创造利润1.54
人去生产新开发的B种产品,根据评估,调配后,继续生产A种产品的员工平均每人每年创造的利润可增加20%,生产B种产品的员工平均每人每年可创造利润1.54 万元。
万元。
(1)调配后,企业生产A种产品的年利润为_________万元,企业生产B种产品的年利润为_________万元(用含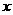 和
和 的代数式表示)。若设调配后企业全年总利润为
的代数式表示)。若设调配后企业全年总利润为 万元,则
万元,则 与
与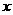 之间的关系式为
之间的关系式为 =____________。
=____________。
(2)若要求调配后,企业生产A种产品的年利润不小于调配前企业年利润的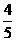 ,生产B种产品的年利润大于调配前企业年利润的一半,应有哪几种调配方案
?请设计出来,并指出其中哪种方案全年总利润最大(必要时,运算过程可保留3个有效数字)。
,生产B种产品的年利润大于调配前企业年利润的一半,应有哪几种调配方案
?请设计出来,并指出其中哪种方案全年总利润最大(必要时,运算过程可保留3个有效数字)。
(3)企业决定将(2)中的年最大总利润(设 =2)继续投资开发新产品。现有6种产品可供选择(不得重复投资同一种产品)各产品所需资金及所获年利润如下表:
=2)继续投资开发新产品。现有6种产品可供选择(不得重复投资同一种产品)各产品所需资金及所获年利润如下表:
|
产
品 |
C |
D |
E |
F |
G |
H |
|
所需资金(万元) |
200 |
348 |
240 |
288 |
240 |
500 |
|
年 利 润(万元) |
50 |
80 |
20 |
60 |
40 |
85 |
如果你是企业决策者,为使此项投资所获年利润不少于145万元,你可以投资开发哪些产品?请写出两种投资方案。
22、如图Rt△ 的两条直角边
的两条直角边 , 点P是边BC上的一动点(P不与B重合)
, 点P是边BC上的一动点(P不与B重合)
以P为圆心作⊙P与BA相切于点M。设 ,⊙P的半径为
,⊙P的半径为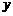
⑴ 求证:△ ∽△
∽△
⑵ 求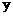 与
与 的函数关系式,并确定当
的函数关系式,并确定当 在什么范围内取值时,⊙P与AC所在直线相离?
在什么范围内取值时,⊙P与AC所在直线相离?
 ⑶ 当点P从点C向点B移动时,是否存在这样的⊙P,使得它与△
⑶ 当点P从点C向点B移动时,是否存在这样的⊙P,使得它与△ 的外接圆相内切?若存在,求出
的外接圆相内切?若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
21、嘉年华游乐场投资150万元引导一项大型游乐设施。若不计维修保养费用,预计开放后每月可创收33万元。而该游乐设施开放后,从第一个月到第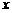 个月的维修费用累计为
个月的维修费用累计为 且
且 ;若将创收扣除投资和维修保养费用后的称为纯收益
;若将创收扣除投资和维修保养费用后的称为纯收益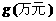 ,
,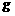 也是关于
也是关于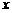 的二次函数。
的二次函数。
⑴
若维修保养费用第一个月为2万元,第二个月为4万元。求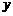 关于
关于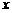 的解析式
的解析式
⑵
求纯收益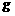 关于
关于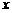 的解析式
的解析式
⑶ 问:设施开放几个月后,游乐场的纯收益达到最大?几个月后能收回投资?

20、课间休息时,同学们到饮水机旁依次每人接水0.25升,他们先打开了一个饮水管,
后来又打开了第二个饮水管。假设接水的过程中每根饮水管出水的速度是匀速的,在
不关闭饮水管的情况下,饮水机水桶内的存水量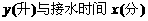 的函数关系图
的函数关系图
像如图所示。请结合图像回答下列问题:
⑴ 存水量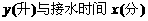 的函数关系式;
的函数关系式;
⑵ 如果接水的同学有28名,那么他们都接完水需要几分钟?
 ⑶ 如果有若干名同学按上述方法接水,他们接水所用时间要比只开第一个饮水管接水的时间少用2分钟,那么有多少名学生接完水?
⑶ 如果有若干名同学按上述方法接水,他们接水所用时间要比只开第一个饮水管接水的时间少用2分钟,那么有多少名学生接完水?

19、如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”,如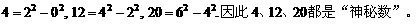
⑴ 28和2012这两个数是“神秘数”吗?为什么?
⑵
设两个连续偶数为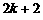 和
和 ,由这两个连续偶数构成的“神秘数”是4的倍数吗?为什么?
,由这两个连续偶数构成的“神秘数”是4的倍数吗?为什么?
⑶ 两个连续奇数的平方差(取正数)是“神秘数”吗?为什么?

18、如图□ABCD中,E为BC边上一点,且AB=AE.
⑴ 求证:△ ≌△
≌△
⑵ 若AE平分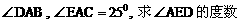

17、


16、如图10,在△ 中AC=CB=2,
中AC=CB=2,
 点,则EC+ED的最小值是 ______
点,则EC+ED的最小值是 ______
15、如图9矩形AOCB的两边 分别位于
分别位于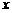 轴,
轴,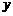 轴上。点B的坐标为
轴上。点B的坐标为 ,
,
D是AB边上一点,将△ 沿直线OD翻折使A点恰好落在对角线OB上的点E处。
沿直线OD翻折使A点恰好落在对角线OB上的点E处。
若点E在一反比例函数的图像上,那么该函数的解析式为 ___________

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com