
题目列表(包括答案和解析)
2、甲、乙两地相距500 km,新修的高速公路开通后,在甲、乙两地问行驶的长途客运车平均速度提高了40%,而从甲地到乙地的时间缩短了2.5 h,求长途客运车原来的平均车速。(结果精确到1 km/h)
l 行程问题:
1) 追及问题:a、两个物体在同一地点不同时间同向出发最后在同一地点的行程问题
等量关系:甲路程=乙路程 甲速度×甲时间=乙速度×(甲时间+乙先走的时间)
b、两个物体从不同地点同时同向出发最后在同一地点的行程问题
等量关系:甲路程-乙路程=原相距路程
2) 相遇问题:两个物体同时从不同地点出发相向而行最后相遇的行程问题
等量关系:甲路程+乙路程=相遇路程 甲速度×相遇时间+乙速度×相遇时间=原两地的路程
3) 一般行程问题:
等量关系:速度×时间=路程
4) 航行问题:
等量关系:顺水速度=静水速度+水流速度 逆水速度=静水速度-水流速度
练习:
1、一队学生去校外进行军事野营训练,他们以5千米/时的速度行进,走了18分钟的时候,学校要将一个紧急通知传给队长,通讯员骑自行车以14千米/时的速度按原路追上去,通讯员用多少时间可以追上学生队伍?
6. 答题。
注:列方程解应用题的关键是找出题中的等量关系
5. 解方程;
4. 根据题中的相等关系列出方程;
3. 列出方程中的有关的代数式;
2. 设未知数,可以直接设未知数,也可以间接设未知数;
1. 认真审题,找出已知量和未知量,以及它们之间的关系;
25.(14分) 如图,在直角坐标系中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线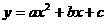 经过点A、B,且
经过点A、B,且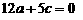 .
.
(1) 求抛物线的解析式;
(2) 如果点P由点A开始沿AB边以2cm/s的速度向点B移动,同时点Q由点B开始沿BC边以1cm/s的速度向点C移动:
① 移动开始后第t秒时,设S=PQ2(cm2),试写出S与t之间的函数关系式,并写出t的取值范围;
②
 当S取得最小值时,在抛物线上是否存在点R,使得以P、B、Q 、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
当S取得最小值时,在抛物线上是否存在点R,使得以P、B、Q 、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
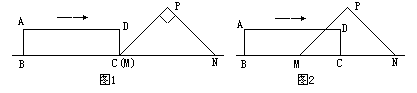
24.(12分)如图,Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上.令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动,直到C点与N点重合为止.设移动x秒后,矩形ABCD与△PMN重叠部分的面积为ycm2,求y与x之间的函数关系式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com