
题目列表(包括答案和解析)
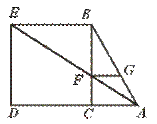
30.已知:如图,在△ABC中,∠C=90°,以BC为边向外作正方形BEDC,连结AE交BC于F,作FG∥BE交AB于G.
求证:FG=FC.
[提示]证明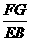 =
=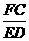 .
.
[答案]∵ FG∥BE,∴ 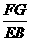 =
=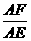 .∵ FC∥ED,∴
.∵ FC∥ED,∴ 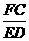 =
=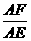 .
.
∴ 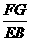 =
=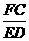 .又 EB=ED,∴ FG=FC.
.又 EB=ED,∴ FG=FC.
29.如图,BD、CE为△ABC的高,求证∠AED=∠ACB.
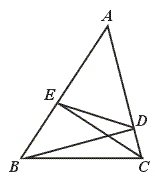
[提示]先证△ABD∽△ACE,再证△ADE∽△ABC.
[答案]∵ ∠ADB=∠AEC=90°,∠A=∠A,
∴ △ABD∽△ACE.∴ 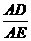 =
=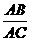 .
.
又 ∠A=∠A,∴ △ADE∽△ABC.∴ ∠AED=∠ACB.
[点评]本题要求运用相似三角形的判定与性质.
28.已知:如图,△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F.求证:BP2=PE·PF.
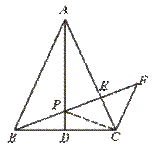
[提示]先证PB=PC,再证△EPC∽△CPF.
[答案]连结PC.
∵ AB=AC,AD是中线,∴ AD是△ABC的对称轴.
∴ PC=PB,∠PCE=∠ABP.∵ CF∥AB,
∴ ∠PFC=∠ABP.∴ ∠PCE=∠PFC.
又 ∠CPE=∠EPC,∴ △EPG∽△CPF.
∴ 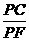 =
=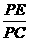 .即 PC2=PE·PF.∴ BP2=PE·PF.
.即 PC2=PE·PF.∴ BP2=PE·PF.
[点评]本题要求运用等腰三角形的性质以及相似三角形的判定与性质.
27.已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.求证:△ADQ∽△QCP.
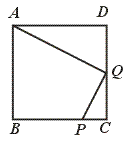
[提示]先证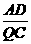 =
=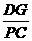 .
.
[答案]在正方形ABCD中,
∵ Q是CD的中点,∴ 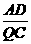 =2.
=2.
∵ 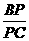 =3,∴
=3,∴ 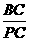 =4.
=4.
又 BC=2DQ,∴ 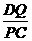 =2.
=2.
在△ADQ和△QCP中,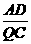 =
=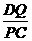 ,∠C=∠D=90°,
,∠C=∠D=90°,
∴ △ADQ∽△QCP.
[点评]本题要求运用相似三角形的判定定理.
26.如图,矩形PQMN内接于△ABC,矩形周长为24,AD⊥BC交PN于E,且BC=10,AE=16,求△ABC的面积.
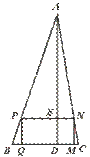
[提示]利用相似三角形的性质,列出关于ED的方程,求ED的长,即可求出S△ABC.
[答案]∵ 矩形PQMN,
∴ PN∥QM,PN=QM.∵ AD⊥BC,
∴ AE⊥PN.∵ △APN∽△ABC,
∴ 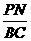 =
=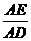 .
.
设ED=x,又 矩形周长为24,则
PN=12-x,AD=16+x.
∴ 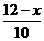 =
=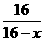 .即 x2+4x-32=0.解得 x=4.
.即 x2+4x-32=0.解得 x=4.
∴ AD=AE+ED=20.∴ S△ABC=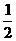 BC·AD=100.
BC·AD=100.
[点评]本题要求运用相似三角形对应高线的比等于相似比.
25.如图,点C、D在线段AB上,△PCD是等边三角形.
(1)当AC、CD、DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数.
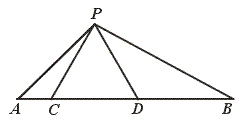
[提示](1)考虑AC、PD、PC、DB之间比例关系.
(2)利用相似三角形的性质“对应角相等”.
[答案]∵ ∠ACP=∠PDB=120°,
当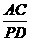 =
=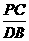 ,即
,即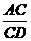 =
=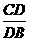 ,也就是CD2=AC·DB时,△ACP∽△PDB.
,也就是CD2=AC·DB时,△ACP∽△PDB.
∴ ∠A=∠DPB.
∴ ∠APB=∠APC+∠CPD+∠DPB
=∠APC+∠A+∠CPD
=∠PCD+∠CPD
=120°.
[点评]本题要求运用相似三角形判定定理和性质的运用.
24.如图,已知△ABC中,AE︰EB=1︰3,BD︰DC=2︰1,AD与CE相交于F,求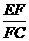 +
+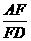 的值.
的值.
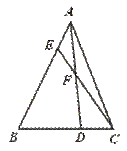
[提示]作EG∥BC交AD于G.
[答案]作EG∥BC交AD于G,则由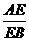 =
=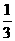 ,即
,即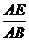 =
=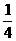 ,得
,得
EG=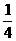 BD=
BD=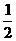 CD,
CD,
∴ 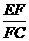 =
=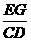 =
=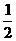 .
.
作DH∥BC交CE于H,则DH=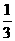 BE=AE.
BE=AE.
∴ 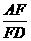 =
=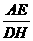 =1,
=1,
∴ 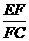 +
+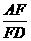 =
=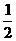 +1=
+1=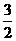 .
.
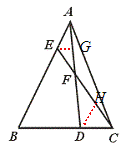
[点评]本题要求灵活运用三角形一边平行线的性质定理.
23.如图,DE∥BC,DF∥AC,AD=4 cm,BD=8 cm,DE=5 cm,求线段BF的长.
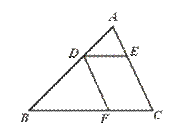
[提示]先求出FC.
[答案]∵ DE∥BC,DF∥AC,
∴ 四边形DECF是平行四边形.
∴ FC=DE=5 cm.
∵ DF∥AC,
∴ 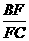 =
=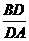 .
.
即 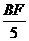 =
=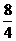 ,
,
∴ BF=10(cm).
[点评]本题要求运用平行四边形判定定理和性质定理、平行线分线段成比例定理.
22.如图,在正方形ABCD中,F是AD的中点,BF与AC交于点G,则△BGC与四边形CGFD的面积之比是_____________.
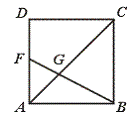
[提示]△BGC∽△FGA,推出FG=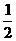 BG,得连结FC.S△BCF=
BG,得连结FC.S△BCF=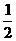 S正方形,再列出
S正方形,再列出
S△CDF与S正方形的关系式.或由△BGC∽△FGA得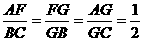 ,所以
,所以
S△AFG=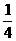 S△BCG=
S△BCG=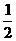 S△AGB,又 S△ACD=
S△AGB,又 S△ACD=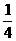 S△ACB,从而得出S四边形CGFD=5S△AFG,
S△ACB,从而得出S四边形CGFD=5S△AFG,
S△BCG=4S△AFG.
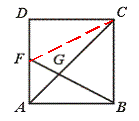
[答案]4︰5.
[点评]本题要求运用相似三角形的基本定理与性质.
21.如图,在△ABC中,M、N是AB、BC的中点,AN、CM交于点O,那么
△MON∽△AOC面积的比是____________.
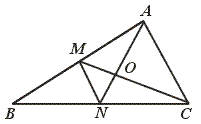
[提示]利用三角形中位线定理.
[答案]1︰4.
[点评]本题要求运用相似三角形的判定、相似三角形的面积比等于相似比的平方,以及三角形的中位线定理.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com