
题目列表(包括答案和解析)
24.  如图,已知AB是⊙O的直径,AC是⊙O的弦,点D是弧ABC中点,弦DE⊥AB,垂足为F,DE交AC于点G.
如图,已知AB是⊙O的直径,AC是⊙O的弦,点D是弧ABC中点,弦DE⊥AB,垂足为F,DE交AC于点G.
(1)图中有哪些相等的线段?(要求:不再标注其他字母,找结论的过程中所作的辅助线不能出现在结论中,不写出推理过程)
(2)若过点E作⊙O的切线ME,交AC的延长线于点M(请补完整图形),试问:ME=MG是否成立?若成立,请证明;若不成立,请说明理由.
(3)在满足第(2)问的条件下,已知AF=3,FB= ,求AG与GM的比.[第(1)的结论可直接利用]
,求AG与GM的比.[第(1)的结论可直接利用]
17、(本小题满分10分)
解:(1)设点P的坐标为 ,则
,则
 PM=
PM= ;
;
又因为点P到直线 的距离为
的距离为 ,
,
所以,以点P为圆心,PM为半径的圆与直线 相切.
(得4分)
相切.
(得4分)
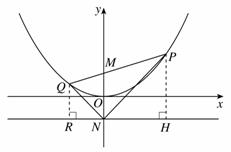
(2)如图,分别过点P,Q作直线 的垂线,垂足分别为H,R.由(1)知,PH=PM,同理可得,QM=QR.
的垂线,垂足分别为H,R.由(1)知,PH=PM,同理可得,QM=QR.
因为PH,MN,QR都垂直于直线 ,所以,PH∥MN∥QR,于是
,所以,PH∥MN∥QR,于是
 ,
,
所以
 ,
,
因此,Rt△ ∽Rt△
∽Rt△ .
.
于是 ,从而
,从而 (得6分)
(得6分)
17.(本小题满分10分).已知点M,N的坐标分别为(0,1),(0,-1),点P是抛物线 上的一个动点.(1)求证:以点P为圆心,PM为半径的圆与直线
上的一个动点.(1)求证:以点P为圆心,PM为半径的圆与直线 的相切;
的相切;
(2)设直线PM与抛物线 的另一个交点为点Q,连接NP,NQ,求证:
的另一个交点为点Q,连接NP,NQ,求证: .
.

24.(1)t= (3分)
(3分)
(2)OC=CP (4分)
过点C作X轴的平行线,交OA与直线BP于点T、H,
证△OTC≌△CHP即可 (7分)
(3)① (0≤t≤1)
(10分)
(0≤t≤1)
(10分)
②当t=0或1时,△PBC为等腰三角形,
即P(1.1), P(1,1- ) (12分 )
) (12分 )
24.如图,点A在Y轴上,点B在X轴上,且OA=OB=1,经过原点O的直线L交线段AB于点C,过C作OC的垂线,与直线X=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:
(1)当△AOC和△BCP全等时,求出t的值。
(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系?并证明你得到的结论。
 (3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围。②求出当△PBC为等腰三角形时点P的坐标。
(3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围。②求出当△PBC为等腰三角形时点P的坐标。
24.(本题满分12分)
如图①、②、③是两个半径都等于2的⊙O1和⊙O2,由重合状态沿水平方向运动到互相外切过程中的三个位置,⊙O1和⊙O2相交于A、B两点,分别连结O1A、O1B、O2A、O2B和AB。
(1)如图②,当∠AO1B=120°时,求两圆重叠部分图形的周长l;(4分)
(2)设∠AO1B的度数为x,两圆重叠部分图形的周长为y,求y关于x的函数关系式,并写出自变量x的取值范围;(4分)
(3)由(2),若y=2x,则线段O2A所在的直线与⊙O1有何位置关系?为什么?除此之外,它们还有其它的位置关系,写出其它位置关系时x的取值范围。(4分)




23、解: (1)在矩形OABC中,设OC=x 则OA= x+2,依题意得
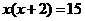 解得:
解得:
 (不合题意,舍去) ∴OC=3, OA=5 … (4分)
(不合题意,舍去) ∴OC=3, OA=5 … (4分)
(只要学生写出OC=3,OA=5即给2分)
(2)连结O′D 在矩形OABC中,OC=AB,∠OCB=∠ABC=90 ,CE=BE=
,CE=BE=
∴ △OCE≌△ABE ∴EA=EO ∴∠1=∠2
在⊙O′中, ∵ O′O= O′D ∴∠1=∠3
∴∠3=∠2 ∴O′D∥AE,
∵DF⊥AE ∴ DF⊥O′D
又∵点D在⊙O′上,O′D为⊙O′的半径 ,
∴DF为⊙O′切线。 … (8分)
(3) 不同意. 理由如下:
25 当AO=AP时,
以点A为圆心,以AO为半径画弧交BC于P1和P4两点
过P1点作P1H⊥OA于点H,P1H = OC = 3,∵A P1= OA = 5
∴A H = 4, ∴OH =1 求得点P1(1,3) 同理可得:P4(9,3) …… (9分)
②当OA=OP时,
同上可求得::P2(4,3),P3( 4,3) …… (11分)
4,3) …… (11分)
 因此,在直线BC上,除了E点外,既存在⊙O′内的点P1,又存在⊙O′外的点P2、P3、P4,它们分别使△AOP为等腰三角形。
…… (12分)
因此,在直线BC上,除了E点外,既存在⊙O′内的点P1,又存在⊙O′外的点P2、P3、P4,它们分别使△AOP为等腰三角形。
…… (12分)
23.(本题满分11分)
如图16,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交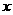 轴于D点,过点D作DF⊥AE于点F.
轴于D点,过点D作DF⊥AE于点F.
(1) 求OA、OC的长;
(2) 求证:DF为⊙O′的切线;
(3)  小明在解答本题时,发现△AOE是等腰三角形.由此,他断定:“直线BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.
小明在解答本题时,发现△AOE是等腰三角形.由此,他断定:“直线BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.
解:
24、解:(1)由已知条件,得:n2-1=0
解这个方程,得: n1=1 ,n2=-1;
当n=1时,得y=x2+x,此抛物线的顶点不在第四象限;
当n=-1时,得y=x2-3x,此抛物线的顶点在第四象限;
∴所求的函数关系式为y=x2-3x …… (4分)
(2)由y=x2-3x,令y=0,得x2-3x=0,解得x1=0 ,x2=3;
∴抛物线与x 轴的另一个交点为(3,0)
∴它的顶点为(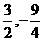 ),对称轴为直线x=
),对称轴为直线x=
①∵BC=1,由抛物线和矩形的对称性易知OB=
∴B(1,0)
∴点A的横坐标x=1,又点A在抛物线y=x2-3x上,
∴点A的纵坐标y=12-3×1=-2。
∴AB=|y |=2
∴矩形ABCD的周长为:2(AB+BC)=6 …… (8分)
②∵点A在抛物线y=x2-3x上,可以设A点的坐标为(x,x2-3x),
∴B点的坐标为 (x,0)。(0<x<
∴BC=3-2x,A在x 轴的下方,
∴x2-3x<0
∴AB=| x2-3x |=3x-x2
∴矩形ABCD的周长P=2((3x-x2)+(3-2x))=-2(x- )2+
)2+
∵a=-2<0
∴当x= 时, 矩形ABCD的周长P最大值是
时, 矩形ABCD的周长P最大值是 。 …… (12分)
。 …… (12分)
24.(本题满分12分)
已知抛物线y=x2+(2n-1)x+n2-1 (n为常数).
(1)当该抛物线经过坐标原点,并且顶点在第四象限时,求出它所对应的函数关系式;
(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点,过A作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于B,DC⊥x轴于C.
①当BC=1时,求矩形ABCD的周长;
②试问矩形ABCD的周长是否存在最大值?如果存在,请求出这个最大值,并指出此时A点的坐标;如果不存在,请说明理由
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com