
题目列表(包括答案和解析)
4、 函数的三种表示方法及用描点法画函数图像。
3、 对函数概念的理解和自变量取值范围的确定。
2、 懂得建立了平面直角坐标系,就使平面上的点与一对有序实数之间建立起一一对应关系,建立数与形之间的联系,初步了解数形结合思想。
1、 掌握x轴、y轴上和四个象限内点的坐标的特征。
函数是数学中的重要概念之一,它使我们从研究不变的量,转化为研究变量之间的相依关系。函数不仅是一个重要的概念,也是一种很重要的数学思想方法。通过函数概念和图象的学习可以用几何图形来解析代数问题,使代数问题变得更形象、直观,便于理解,另一方面,也可以用代数方法来研究几何问题。
本章内容包括三个单元。第一单元是直角坐标系的初步知识,第二单元是函数及其图象,第三单元是常见的几种函数,包括一次函数(正比例函数)、二次函数、反比例函数及其图象。(本讲主要学习巩固第一、二单元,第三单元留待下学期复习)。
学习直角坐标系,建立有序实数与平面内的点的一一对应关系,为研究函数的图象作准备。学习函数概念,首先要了解常量、变量概念,用动态的观点来看问题。弄清函数的本质是具有某些特点的对应关系,抓住函数对自变量的依从关系就是函数与自变量的对应关系。函数关系中自变量的取值范围是函数存在的不可缺少的部分。
了解函数有三种表示方法,即解析法、列表法和图象法。能正确迅速地列表、描点并绘出函数图象,(以下为下学期内容)要逐步学会用图象总结函数的性质,由函数的性质能想象出表达式中自变量x与函数y的变化情况。
本章重点是函数的概念、函数解析式与图象性质的内在联系。能灵活地进行数与形之间的变换是难点。
3、 能画出简单函数的图象;知道不仅可以用解析法,而且还可以用列表法和图象法表示函数。
2、 能分清实例中出现的常量与变量、自变量与函数;对简单的函数表达式,能确定自变量的取值范围,并会求出函数值。
1、 能正确画出直角坐标系;并能在直角坐标系中,根据点的坐标找出点,由点求出点的坐标。
13、
解:令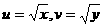 ,则原方程组可化为
,则原方程组可化为 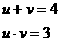
(方法一)由u+v=4得:u=4-v,代入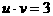 ,得:
,得: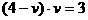
即:v2-4v+3=0 ∴v1=1,v2=3
代回u=4-v,得: 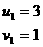
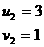 即:
即: 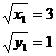
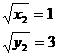
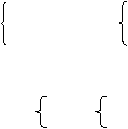 ∴
∴ 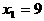 x2=1
x2=1
y1=1 y2=9
(方法二)根据一元二次方程根与系数的关系,可把u、v看成是关于t的一元二次方程t2-4t+3=0的两个实数根t1=1,t2=3
∴可得 u1=1 u2=3,以下解法同(解法一)。
v1=3 v2=1
12、
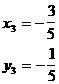
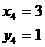
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com