10．三角形的内心是用“三角形的内切圆的圆心”来定义的，由于三角形的内心就是三角形三个内角平分线的交点，所以当三角形的内心已知时，过三角形顶点和内心的射线，必平分三角形的内角。

9．　 任意三角形都有且只有一个内切圆(因为圆心是唯一确定的，半径只有一个定长)，而任意多边形不一定有内切圆。

8．　 切线的性质主要有如下五个：

(1) 　 切线和圆有且只有一个公共点；

(2) 　 切线和圆心的距离等于该圆的半径；

(3) 　 圆的切线垂直于过切点的半径；

(4) 　 经过圆心垂直于切线的直线必过切点；

(5) 　 经过切点垂直于切线的直线必过圆心。

其中，(1) 是切线的定义；(2) 是判定方法的逆命题；(3)、(4)、(5)即为课本上的性质定理及其推论。

7．　 判定一条直线是圆的切线有三种方法：

(1) 　 和圆有且只有一个公共点的直线是圆的切线；

(2) 　 和圆心距离等于该圆半径的直线是圆的切线；

(3) 　 过半径的外端且垂直于这条半径的直线是圆的切线。

其中(1) 是切线的定义；(2) 和(3) 本质相同，表达形式不同。解题时，可根据题目的特点选择适当的判定方法。

6．　 在运用切线的判定和性质定理时，常常需要添加辅助线，一般规律为：

(1) 　 已知一条直线是某圆的切线时，切点的位置一般是确定的。在写已知条件时，应交待直线和圆相切于哪一点，辅助线常常是连结圆心和切点，得到半径，从而得出“切线垂直于半径”的结论。

(2) 　 要证明某直线是圆的切线时，如果已知直线过圆上某一点，则可以作出这一点的半径，证明直线垂直于半径；如果直线与圆的公共点没有确定，常常过圆心作直线的垂线，证明圆心到直线的距离等于半径。

5．　 切线的性质有一个定理和两个推论，其中定理用途较广泛，必须熟练掌握。实际上，(1) 垂直于切线；(2) 过切点；(3) 过圆心。这三个条件中，知道任意两个，就可以得出第三个。

4．　 对于切线的判定定理，必须分清定理的题设和结论，“经过半径的外端”和“垂直于这条半径”这两个条件缺一不可，否则便不是圆的切线。

3．　 直线和圆的位置关系既可以用它们的交点的个数来区分，也可以用圆心到直线的距离与圆的半径的大小来区分，两种方式是一致的。

2．　 由直线和圆的三种位置关系可以直观的得到圆心到直线的距离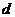与圆半径的数量关系：

(1) 　 直线和⊙O相交Û＜，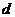

(2) 　 直线和⊙O相切Û＝，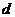

(3) 　 直线和⊙O相离Û＞；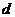

这三个结论，既可以作为直线和圆的各种位置关系的判定，又可作为性质。

1．　 在切线的定义中，要准确理解“直线和圆有唯一公共点”的含义，它是指有一个并且只有一个公共点，与“直线和圆有一个公共点”的含义不同，避免出现“直线和圆有一个公共点时叫直线和圆相切”的错误。