
题目列表(包括答案和解析)
28.(8分)如图,已知ABCD是圆内接四边形,EB是⊙O的直径,且EB⊥AD,AD与BC的延长线交于F,求证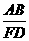 =
=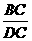 .
.
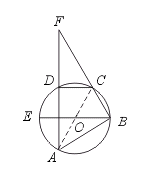 [提示]连结AC,证△ABC∽△FDC.显然∠FDC=∠ABC.因为AD⊥直径EB,由垂径定理得
[提示]连结AC,证△ABC∽△FDC.显然∠FDC=∠ABC.因为AD⊥直径EB,由垂径定理得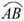 =
=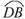 ,故∠DAB=∠ACB.又因为∠FCD=∠DAB,所以
,故∠DAB=∠ACB.又因为∠FCD=∠DAB,所以
∠FCD=∠ACB,故△ABC∽△FDC,则可得出待证的比例式.
[略证]连结AC.∵ AD⊥EB,且EB为直径,∴ 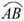 =
=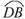 .
.
∴ ∠ACB=∠DAB.∵ ABCD为圆内接四边形,∴ ∠FCD=∠DAB,∠FDC=∠ABC.
∴ ∠ACB=∠FCD.∴ △ABC∽△FDC.∴ 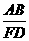 =
=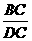 .
.
27.(8分)如图,AB为⊙O的直径,P为BA的延长线上一点,PC切⊙O于点C,
CD⊥AB,垂足为D,且PA=4,PC=8,求tan ∠ACD和sin ∠P的值.
[提示]连结CB,易证△PCA∽△PBC,所以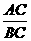 =
=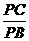 .由切割线定理可求PB的长,所以
.由切割线定理可求PB的长,所以
tan∠ACD=tan ∠CBA=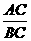 =
=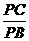 .
. 连结OC,则在Rt△OCP中可求
连结OC,则在Rt△OCP中可求
sin∠P的值.
[略解]连结OC、BC.∵ PC为⊙O的公切线,∴ PC2=PA·PB.
∴ 82=4·PB.∴ PB=16.∴ AB=16-4=12.易证△PCA∽△PBC.∴ 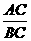 =
=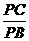 .∵ AB为⊙O的直径,∴ ∠ACB=90°.又 CD⊥AB,∴ ∠ACD=∠B.∴ tan ∠ACD=tan B=
.∵ AB为⊙O的直径,∴ ∠ACB=90°.又 CD⊥AB,∴ ∠ACD=∠B.∴ tan ∠ACD=tan B=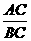 =
=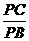 =
=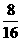 =
=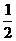 .
.
∵ PC为⊙O的切线,∴ ∠PCO=90°.∴ sin P=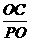 =
=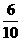 =
=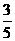 .
.
26.(8分)如图,⊙O的直径AB和弦CD相交于点E,且AE=1 cm,EB=5 cm,
∠DEB=60°,求CD的长.
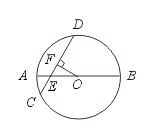
[分析]因为AE=1 cm,EB=5 cm,所以OE=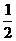 (1+5)-1=2(cm).在Rt△OEF中可求EF的长,则EC、ED都可用DF表示,再用相交弦定理建立关于DF的方程,解方程求DF的长.
(1+5)-1=2(cm).在Rt△OEF中可求EF的长,则EC、ED都可用DF表示,再用相交弦定理建立关于DF的方程,解方程求DF的长.
[略解]∵ AE=1 cm,BE=5 cm,∴ ⊙O的半径为3 cm.∴ OE=3-1=2(cm).在Rt△OEF中,∠OEF=60°,∴ EF=cos 60°·OE=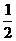 ·2=1(cm).∵ OF⊥CD,∴ FC=FD.∴ EC=FC-FE=FD-FE,ED=EF+FD.即 EC=FD-1,ED=FD+1.由相交弦定理,得 AE·EB=EC·ED.∴ 1×5=(FD-1)(FD+1).解此方程,得 FD=
·2=1(cm).∵ OF⊥CD,∴ FC=FD.∴ EC=FC-FE=FD-FE,ED=EF+FD.即 EC=FD-1,ED=FD+1.由相交弦定理,得 AE·EB=EC·ED.∴ 1×5=(FD-1)(FD+1).解此方程,得 FD=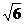 (负值舍去).∴ CD=2FD=2
(负值舍去).∴ CD=2FD=2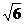 (cm).
(cm).
25.平分弦的直径垂直于弦……………………………………………………………( )[答案]×.
[点评]当被平分的弦为直径时,两直径不一定垂直.
24.三角形一定有内切圆………………………………………………………………( )[答案]√.
[点评]作三角形的两条角平分线,设交点为I,过I作一边的垂线段,则以点I为圆心,垂线段长为半径的圆即三角形的内切圆.
23.正五边形既是轴对称图形,又是中心对称图形…………………………………( )[答案]×.
[点评]正五边形是轴对称图形,但不是中心对称图形.
22.各角都相等的圆内接多边形是正多边形…………………………………………( )[答案]×.
[点评]矩形内接于以对角线为直径的圆,但它不是正多边形.
21.相交两圆的公共弦垂直平分连结这两圆圆心的线段……………………………( )[答案]×.
[点评]相交两圆的连心线垂直平分公共弦,反过来公共弦不一定平分连结两圆圆心的线段.
20.用一张面积为900 cm2的正方形硬纸片围成一个圆柱的侧面,则这个圆柱的底面直径
为_____.
[提示]面积为900 cm2的正方形的边长为30 cm,则底面圆的周长30 cm.设直径为d,则pd=30,故d=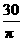 (cm).[答案]
(cm).[答案]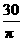 cm.
cm.
19.扇形的半径为6 cm,面积为9 cm2,那么扇形的弧长为______,扇形的圆心角度数为_____.
[提示]已知扇形面积为9 cm2,半径为6 cm,则弧长l=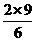 =3;设圆心角的度数为n,则
=3;设圆心角的度数为n,则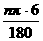 =3 cm,所以n=
=3 cm,所以n=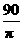 .[答案]3;
.[答案]3;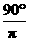 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com