
题目列表(包括答案和解析)
(二)1.了解平面直角坐标系的有关概念,会由点的位置确定点的坐标,会由点的 坐标确定点的位置.
2.理解函数的意义,能根据一个具体的函数解析式,确定自变量的取值范围, 并会由自变量的值求出函数值.
3.掌握正比例函数、反比例函数、一次函数、二次函数的概念及性质,会画出 图象.
4.能根据不同条件,用待定系数法求函数解析式.
(一)1.理解锐角三角函数定义,会用锐角三角形定义列出函数关系式解直角三角形.
2.了解锐角三角函数的四个同角间的函数恒等式,并会解一些相关的题目.
3.理解锐角三角函数的性质,会比较在某个范围内正弦和正弦,正弦和余弦, 正切和正切,正切和余切的大小,及利用函数值的大小判断角的大小.
4.熟记特殊角的三角函数组,并会准确的计算.
5.会用解直角三角形的有关知识,解某些实际问题.
3.化简,计算:
⑴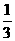 ⑵
⑵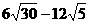 ⑶
⑶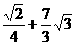 ⑷10 ⑸
⑷10 ⑸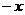
⑹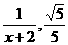 ⑺∵
⑺∵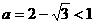 ∴原式=
∴原式=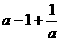
⑻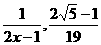 ⑼-1 ⑽
⑼-1 ⑽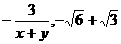
2.填空题:
(1)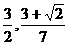 (2)
(2)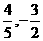 (3)
(3)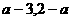 (4)
(4)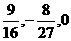 (5)0或1
(5)0或1
(6)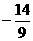 (7)
(7)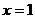 (8)
(8)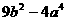 9)
9)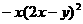 (10)
(10)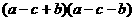 (11)
(11)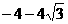 (12)3 (13)
(12)3 (13)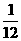 (14)0.1402 (15)
(14)0.1402 (15)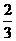 (16)
(16)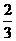 (17)
(17)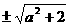 (18)
(18)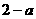 (19)
(19)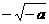 (20)
(20)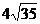 (21)1999
(21)1999
1.判断题:
⑴× ⑵× ⑶√ ⑷× ⑸× ⑹×
⑺× ⑻√ ⑼√ ⑽× ⑾√ ⑿√
3.化简,计算:
⑴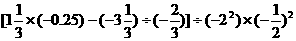
⑵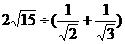 ⑶
⑶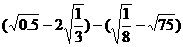
⑷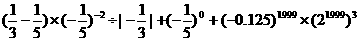
⑸当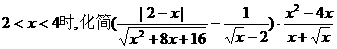
⑹先化简后求值: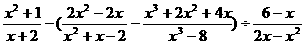
⑺当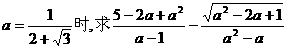 的值
的值
⑻已知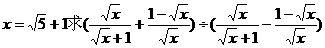 的值
的值
⑼当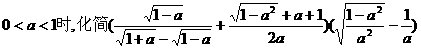
⑽化简,求值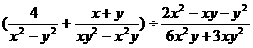
2.填空题:
(1)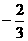 的倒数的相反数是_____;
的倒数的相反数是_____;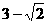 的倒数是_____.
的倒数是_____.
(2)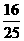 的算术平方根是_____;
的算术平方根是_____;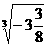 =_____.
=_____.
(3)若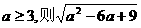 ;若
;若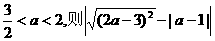 化简的结果是_____.
化简的结果是_____.
(4)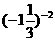 = _____;
= _____;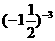 =_____;
=_____;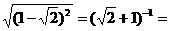 _____.
_____.
(5)当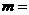 _____时,
_____时,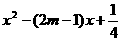 是完全平方式.
是完全平方式.
(6)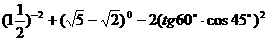 = _____.
= _____.
(7)分式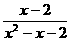 无意义而分式
无意义而分式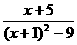 有意义的条件是_____.
有意义的条件是_____.
(8)计算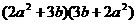 的结果是_____.
的结果是_____.
(9)分解因式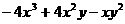 的结果是_____.
的结果是_____.
(10)分解因式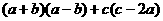 的结果是_____.
的结果是_____.
(11)若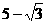 的整数部分是
的整数部分是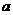 ,小数部分是
,小数部分是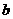 ,则代数式
,则代数式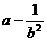 的值是_____.
的值是_____.
(12)当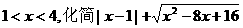 的结果是_____.
的结果是_____.
(13)若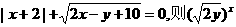 的值是_____.
的值是_____.
(14)已知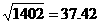 ,
,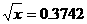 ,则
,则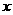 =_____.
=_____.
(15)已知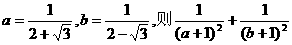 的值是_____.
的值是_____.
(16)若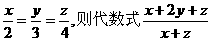 的值是_____.
的值是_____.
(17)若一个正偶数的算术平方根是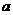 ,那么和这个正偶数相邻的下一个正偶数的平方根是_____.
,那么和这个正偶数相邻的下一个正偶数的平方根是_____.
(18)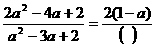
(19)将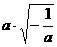 根号外面的因式移到根号内的结果是_____.
根号外面的因式移到根号内的结果是_____.
(20)若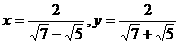 ,则
,则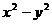 的值是_____.
的值是_____.
(21)计算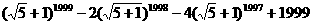 的结果是_____.
的结果是_____.
1.判断题:
⑴整数和小数统称有理数( )
⑵平方根等于它自己的数是1或0( )
⑶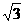 是3的平方根( )
是3的平方根( )
⑷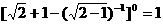 ( )
( )
⑸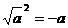 成立的条件是
成立的条件是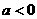 ( )
( )
⑹若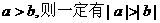 ( )
( )
⑺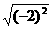 的平方根是±2( )
的平方根是±2( )
⑻将0.0000357用科学记数法表示成3.57×10-5( )
⑼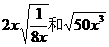 是同类二次根式( )
是同类二次根式( )
⑽如果分式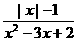 的值为零,那么
的值为零,那么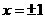 ( )
( )
⑾若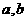 互为相反数,
互为相反数,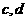 互为倒数,
互为倒数, 的绝对值是2,那么
的绝对值是2,那么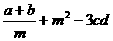 的值是( )
的值是( )
⑿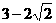 的有理化因式是
的有理化因式是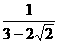 ( )
( )
12.二次根式:
①定义: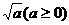 叫二次根式.
叫二次根式.
②性质: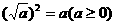
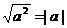
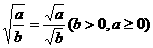
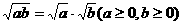
③同类二次根式被开方数相同的二次根式.
④最简二次根式满足(1)根号内无分母(2)根号内再也没有能开得尽方的因
式
⑤二次根式的加减法:合并同类二次根式.
⑥二次根式乘法: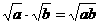
⑦二次根式除法: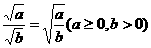
⑧分母有理化:分母,分子同乘以分母的有理化因式.
11.数的开平方
①定义:若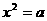 ,
,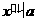 的平方根,记作
的平方根,记作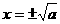 .
.
②性质:一个正数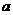 有两个平方根,
有两个平方根,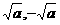 ;负数没有平方根;零的平方根 是零.
;负数没有平方根;零的平方根 是零.
③算术平方根:一个正数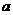 的正的平方根
的正的平方根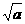 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com