
题目列表(包括答案和解析)
7、如果x1、x2是方程2x2-6x+3=0的两个根,那么x12+x22=______。
6、设x1、x2是方程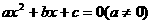 的两个根,则
的两个根,则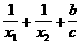 =______。
=______。
5、一元二次方程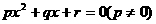 的两个根为0和-1,则
的两个根为0和-1,则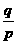 =______。
=______。
4、m取______时,方程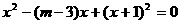 有两个不相等的实数根。
有两个不相等的实数根。
3、当k为______时,关于x的方程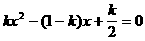 有实根。
有实根。
2、当m=______时,关于x的方程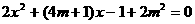 有两个相等的实数根。
有两个相等的实数根。
1、已知方程 的一个根是
的一个根是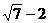 ,则方程的另一根是______,m=______。
,则方程的另一根是______,m=______。
6.一元二次方程的应用,一般分三种类型的题目
①如两个连续偶数之积是168,求这两个数;
 ②面积问题.
②面积问题.
如利用墙的一边,以长为28米的铁丝
网围成一个面积是96m2的矩形养鸡场,墙的
长度是15米,求鸡场的长和宽.
解:设宽为x米,则长是(28-2x)米
由题意得:x(28-2x)=96 2x2-28x+96=0
x2-14x+48=0 x1=6 x2=8
但x=6不合题意,(因为若宽为6米,则长是16米,长于墙的长度不行.)
28-2x=12
答:鸡场的长12米,宽8米.
③百分率问题.
原数(1+增长率)n=增长到的数 (n是连续增长次数,设每一次增长率相同)
例1. 某厂一月份销售额20万元,到三月份销售额达到26.45万元,求每月的增长率.
解:设增长率是x
由题意得20(1+x)2=26.45
例2. 某印刷厂一月份印书50万册.第一季度共印刷了182万册,求每月的增长率.
注意此题和例1不同,182万是1月印数+2月印数+3月印数=182
一月份50 二月份50(1+x) 三月份50(1+x)2
∴50+50(1+x)+50(1+x)2=182
因复习讲稿篇幅过长,望同学们很好看讲稿,关于综合复习题,我们将在10月底提供给大家.
5.二次三项式ax2+bx+c的因式分解
若x1,x2是ax2+bx+c=0的根
则ax2+bx+c=a(x-x1)(x-x2)
注意问题:①因式分解要记作分解公式
②令ax2+bx+c=0求根
(若Δ<0,方程无实根,说明不能在实数范围内分解)
4.一元二次方程的根与系数之间的关系.
设x1,x2是ax2+bx+c=0(a≠)的两根,
则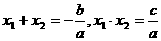 ,它的应用有:
,它的应用有:
①已知方程的一个根,求另一根及k(或m)的值.
如已知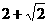 是x2+kx+2=0的一个根,求另一根k的值.
是x2+kx+2=0的一个根,求另一根k的值.
解:设另一根是x,则由题意得
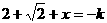 ①
① 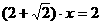 ②
② 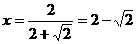
代入①式得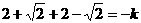 ∴k=-4
∴k=-4
∴k的值是-4,另一根是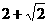 .
.
②利用根与系数的关系求某些代数式的值.
如已知x1,x2是方程2x2-3x-1=0的根.
求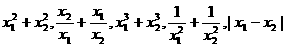 的值.
的值.
此类题目是一元二次方程根与系数间的关系应用的基础,充分利用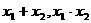 ,这就要将这些代数式变形成能用
,这就要将这些代数式变形成能用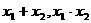 的形式.
的形式.
如将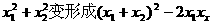
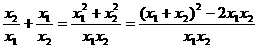
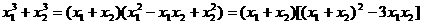
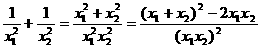

③求某些字母的值.
如已知x1,x2是2x2-mx-30=0的根,且5x1+3x2=0,求m的值.
解:由一元二次方程根与系数间的关系
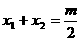 ①
① 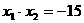 ②
②
由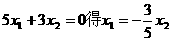
代入①式得: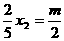
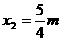 ∴
∴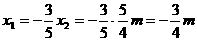
将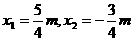 代入②式得:
代入②式得:
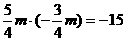
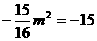
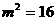

④建立方程.
以x1,x2为根的方程是x2-(x1+x2)x+x1x2=0.要求熟记此公式.
若要以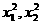 为根作一个方程就是
为根作一个方程就是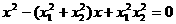 .
.
要以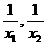 为根作一个方程就是
为根作一个方程就是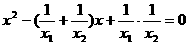 .
.
如已知方程2x2-5x-3=0
求作一个新的方程,使它的根分别是原方程根的①平方;②相反数;③3倍.
解:设x1,x2是2x2-5x-3=0的根
则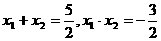
①所求方程是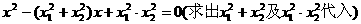
即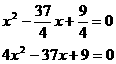
②所求方程是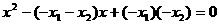
即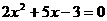
③所求方程是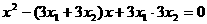
即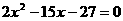
⑤杂题.如已知方程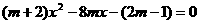
m为何值两根互为相反数(x1+x2=0,Δ>0)
m为可值两根互为例数(x1·x2=1,Δ>0)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com