
题目列表(包括答案和解析)
13.解:若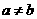 ,则可知
,则可知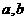 为方程
为方程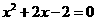 的两实数根,由韦达定理得a+b=-2,ab=-2. ∴
的两实数根,由韦达定理得a+b=-2,ab=-2. ∴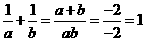
若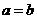 ,则解关于a,b的方程分别得
,则解关于a,b的方程分别得
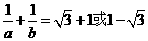 .
.
11.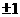 12.三
12.三
6.15°或105° 7.14或2 8.3 9.4或5 10.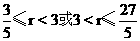
1.C 2.D 3.C 4.C 5.D
4.解:(1)可设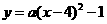 . ∵交y轴于点C(0,3),∴3=16a-1,∴
. ∵交y轴于点C(0,3),∴3=16a-1,∴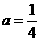 .
.
∴抛物线的解析式为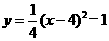 ,即
,即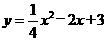 .
.
(2)存在
当y=0时,则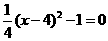 ,∴
,∴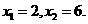 ∴A(2,0),B(6,0).
∴A(2,0),B(6,0).
设P(0,m),则OP= . 在△AOC与△BOP中,
. 在△AOC与△BOP中,
①若∠OCA=∠OBP,则△BOP∽△COA,∴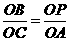 .
.
OP=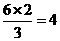 ,∴
,∴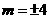 .
.
②若∠OCA=∠OPB,则△BOP∽△AOC,∴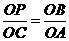 .
.
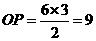 ,∴
,∴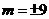 .
.
∴存在符合题意的点P,其坐标为(0,4)、(0,-4)、(0,9)或(0,-9)
中考零距离答案
3.解:(1)当x=0时,y=4. 当y=0时,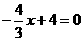 ,∴x=3.
,∴x=3.
∴M(3,0),N(0,4)
(2)①当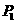 点在y轴上,并且在N点的下方时,设⊙
点在y轴上,并且在N点的下方时,设⊙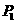 与直线
与直线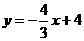 相切于点A,连接
相切于点A,连接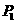 A,则
A,则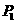 A⊥MN.
A⊥MN.
∴∠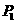 AN=∠MON=90°,∵∠
AN=∠MON=90°,∵∠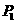 NA=∠MNO,∴△
NA=∠MNO,∴△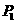 AN∽△MON,∴
AN∽△MON,∴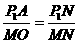
在Rt△OMN中,OM=3,ON=4,∴MN=5.
又∵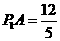 ,∴
,∴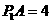 ,∴
,∴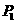 点坐标是(0,0)
点坐标是(0,0)
②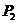 点在x轴上,并且在M点的左侧时,同理可得
点在x轴上,并且在M点的左侧时,同理可得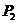 点坐标是(0,0)
点坐标是(0,0)
③当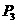 在x轴上,并且在M点的右侧时,设⊙
在x轴上,并且在M点的右侧时,设⊙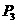 与直线
与直线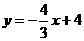 相切于点B,连接
相切于点B,连接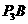 ,则
,则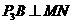 ∴OA//
∴OA//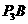 . ∵OA=
. ∵OA=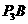 ,∴
,∴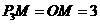 .
.
∴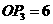 ,∴
,∴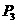 点坐标是(6,0)
点坐标是(6,0)
④当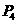 点在y轴上,并且在点N上方时,同理可得
点在y轴上,并且在点N上方时,同理可得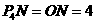 .
.
∴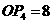 . ∴
. ∴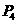 点坐标是(0,8)
点坐标是(0,8)
综上,P点坐标是(0,0),(6,0),(0,8).
2.(1)当点P运动2秒时,AP=2cm,由∠A=60°,知AE=1,PE=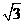 .∴
.∴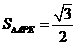 .
.
(2)①(i)当0≤t≤6时,点P与点Q都在AB上运动,设PM与AD交于点G,QN与AD交于点F,则AQ=t,AF=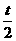 ,QF=
,QF=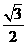 ,AP=t+2,AG=1+
,AP=t+2,AG=1+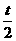 ,PG=
,PG=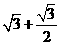 .
.
∴此时两平行线截平行四边形ABCD的面积为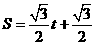 .
.
(ii)当6≤t≤8时,点P在BC上运动,点Q仍在AB上运动,设PM与DC交于点G,QN与AD交于点F,则AQ=t,AF=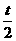 ,DF=4-
,DF=4-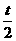 ,QF=
,QF=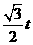 ,BP=t-6,
,BP=t-6,
CP=10-t,PG=(10-t)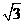 .
.
而BD=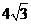 ,故此时两平行线截平行四边形ABCD的面积为
,故此时两平行线截平行四边形ABCD的面积为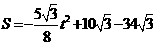 .
.
(iii)当8≤t≤10时,点P和点Q都在BC上运动,设PM与DC交于点G,QN与DC交于点F,则CQ=20-2t,OF=(20-2t),CP=10-t,PG=(10-t)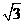 .
.
∴此时两平行线截平行四边形ABCD的面积为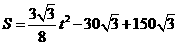 .
.
故S关于t的函数关系式为
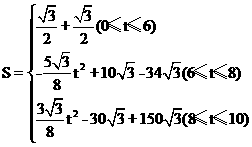
②(附加题)当0≤t≤6时,S的最大值为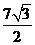 ;
;
当6≤t≤8时,S的最大值为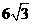 .
.
当8≤t≤10时,S的最大值为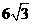
所以当t=8时,S有最大值为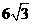 .
.
1.解:(1)∵方程有实数根.∴①当k=0时,原方程变为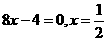 ,方程有实数根.
,方程有实数根.
②当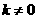 时,
时,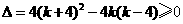 ,解之得
,解之得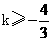 ,∴
,∴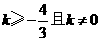 故k的取值范围是
故k的取值范围是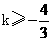 .
.
(2)①若b=c,则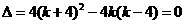 ,解得
,解得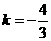 ,此时方程的根为b=c=2,又∵a=3,满足三角形三边关系,∴
,此时方程的根为b=c=2,又∵a=3,满足三角形三边关系,∴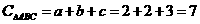
②若a=b或a=c,则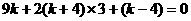 ,∴
,∴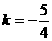 ,此时方程另一根为:
,此时方程另一根为: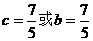 ,满足三角形三边关系,∴
,满足三角形三边关系,∴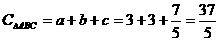 .
.
17.(2004 黄冈)在直角坐标系XOY中,O为坐标原点,A、B、C三点的坐标分别为A(5,0),B(0,4),C(-1,0),点M和点N在x轴上,(点M在点N的左边)点N在原点的右边,作MP⊥BN,垂足为P(点P在线段BN上,且点P与点B不重合)直线MP与y轴交于点G,MG=BN.
(1)求经过A、B、C三点的抛物线的解析式.(2)求点M的坐标.
(3)设ON=t,△MOG的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
(4)过点B作直线BK平行于x轴,在直线BK上是否存在点R,使△ORA为等腰三角形?若存在,请直接写出R的坐标;若不存在,请说明理由.
变式思考答案
16.(2003 烟台)在直角坐标系中,有以A(-1,-1),B(1,-1),C(1,1),D(-1,1)为顶点的正方形,设正方形在直线y=x上方及直线
y=-x+2a上方部分的面积为S,(1)求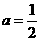 时,S的值.(2)a在实数范围内变化时,求S关于a的函数关系式.
时,S的值.(2)a在实数范围内变化时,求S关于a的函数关系式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com