
题目列表(包括答案和解析)
16.去年年底,东南亚地区发生海啸,给当地人民带来了极大的灾难。听到
这个消息,某校初中毕业班中的30名同学踊跃捐款,支援灾区人民。其中女同学共捐款150元,男同学共捐款120元,男同学比女同学平均每人少捐款2元,男、女同学平均每人各捐款多少元?
[解]设男同学平均每人捐款x元。
依题意: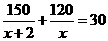 ,解得:x=8(x= -1是增根)。
,解得:x=8(x= -1是增根)。
15.为了美化眉山市区环境,打造中国西部最美的外滩,欲将东坡湖进行清淤疏通改造,现有两家清淤公司可供选择,这两家公司提供如下信息:
⑴ 若东坡湖首批需要清除的淤泥面积大约为1.2万平方米,平均厚度约为0.4,那么请哪个清淤公司进行清淤费用较省,请说明理由。
⑵ 若甲公司单独做了2天,乙公司单独做了3天,恰好完成全部清淤任务的一半;若甲公司先做2天,剩下的清淤工作由乙公司单独完成,则乙公司所用时间恰好比甲公司单独完成清淤任务所用时间多1天。甲、乙两公司单独完成清淤任务各需多少天?
[解] ⑴ 解:淤泥体积:1.2×104×0.4=4800m3 甲公司的收费:18×4800+5000=91400元 乙公司的收费:20×4800=96000元 91400元<96000元
答:应请甲公司负责清淤工作。
⑵ 解:设单独完成清淤工作,甲公司需x天,乙公司需y天,根据题意得
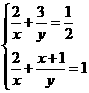
解这个方程组②-①得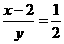 ,即y=2x-4 ③把③代入①得x2-9x+8=0 解之得x1=8,x2=1 当x=1时,y=2x-4<0 不合题意
,即y=2x-4 ③把③代入①得x2-9x+8=0 解之得x1=8,x2=1 当x=1时,y=2x-4<0 不合题意
当x=8时,y=2x-4=12 经检验x=8,y=12是方程组的解
答:单独完成清淤工作,甲公司需8天,乙公司需12天
14.《中华人民共和国道路交通安全法实施条例》中规定:超速行驶属违法行为。为确保行车安全,一段高速公路全程限速110千米/时(即人一时刻的车速都不能超过110千米/时。以下是张师傅和李师傅行驶完这段全程为400千米的高速公路时的对话片断。张:“你的车速太快了,平均每小时比我多跑20千米,少用我一个小时就跑完了全程,还是慢点。”李:“虽然我的时速快,但最大时速不超过我平均时速的10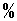 ,可没有超速违法啊。”李师傅超速违法吗?为什么?
,可没有超速违法啊。”李师傅超速违法吗?为什么?
[解]设李师傅的平均速度为x千米/时,则张师傅的平均速度为(20-x)千米/时,
根据题意,得 - =1
去分母,整理,得 x2- 20x- 8000=0
x1=100,x2=-80
经检验,x1=100,x2=-80都是所列方程的根,但x2=-80不符合题意,舍去。
∴x=100,
∴李师傅的最大时速是:100(1+10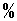 )=110。
)=110。
∴李师傅行驶途中的最大时速在限速范围内,他没有超速违法。
13.小明计划将今年春节期间得到的压岁钱的一部分作为自己一年内购买课外书籍的费用,其余的钱计划买些玩具去看望市福利院的孩子们。某周日小明在商店选中了一种小熊玩具,单价是10元,按原计划买了若干个,结果他的压岁钱还余30%,于是小明又多买了6个小熊玩具,这样余下的钱仅是压岁钱的10%。
(1)问小明原计划买几个小熊玩具,小明的压岁钱共有多少元;
(2)为了保证小明购书费用不少于压岁钱的20%,问小明最多可比原计划多买几个小熊玩具。
[解](1)小明原计划买21个小熊玩具;
(2)3个。
12. 今年五月,某工程队(有甲、乙两组)承包人民路中段的路基改造工程,规定若干天内完成.
(1)已知甲组单独完成这项工程所需时间比规定时间的2倍多4天,乙组单独完成这项工程所需时间比规定时间的2倍少16天.如果甲、乙两组合做24天完成,那么甲、乙两组合做能否在规定时间内完成?
(2)在实际工作中,甲、乙两组合做完成这项工程的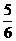 后,工程队又承包了东段的改造工程,需抽调一组过去,从按时完成中段任务考虑,你认为抽调哪一组最好?请说明理由.
后,工程队又承包了东段的改造工程,需抽调一组过去,从按时完成中段任务考虑,你认为抽调哪一组最好?请说明理由.
[解](1)设规定时间为x天,则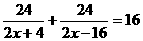
解之,得x1=28,x2=2.
经检验可知,x1=28,x2=2都是原方程的根,
但x2=2不合题意,舍去,取x=28.
由24<28知,甲、乙两组合做可在规定时间内完成.
(2) 设甲、乙两组合做完成这项工程的5/6用去y天,
则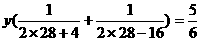 解之,得y=20(天).(5分)
解之,得y=20(天).(5分)
甲独做剩下工程所需时间:10(天).
因为20+l0=30>28,
所以甲独做剩下工程不能在规定时间内完成;
乙独做剩下工程所需时间:20/3(天).
因为20+20/3=26 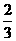 <28,
<28,
所以乙独做剩下工程能在规定时间内完成.
所以我认为抽调甲组最好.
11.某工程,甲工程队单独做40天完成,若乙工程队单独做30天后,甲、乙两工程队再合作20天完成。
(1)求乙工程队单独做需要多少天完成?
(2)将工程分两部分,甲做其中一部分用了x天,乙做另一部分用了y天,其中x、y均为正整数,且x<15,y<70,求x、y.
[解](1)设乙工程队单独做需要x天完成。
则30×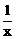 +20(
+20(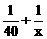 )=1,解之得:x=100
)=1,解之得:x=100
经检验得x=100是所列方程的解,所以求乙工程队单独做需要100天完成。
(2)甲做其中一部分用了x天,乙做另一部分用了y天
所以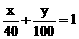 ,即:y=100 -
,即:y=100 -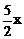 ,又x<15,y<70
,又x<15,y<70
所以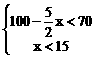 ,解之得:12<x<15,所以x=13或14,
,解之得:12<x<15,所以x=13或14,
又y也为正整数,所以x=14,y=65
10.解方程: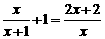
[解]原方程可化为: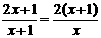 , ∴ x (2x+1)=2 (X+1)2
, ∴ x (2x+1)=2 (X+1)2
解得: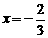
经检验可知,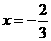 的原方程的解。
的原方程的解。
9.解分式方程: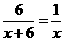
[解]两边同时乘以 x ( x + 10 ) ,解得:6 x = x + 10
5 x = 10 x = 2
经检验:x = 2-是原方程的解
8. 用换元法解方程: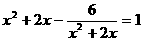
[解]设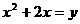 ,那么
,那么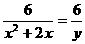 , 于是原方程变形为
, 于是原方程变形为 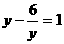
方程的两边都乘以y,约去分母,并整理,得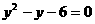
解这个方程,得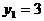 ,
,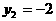
当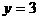 时,
时,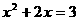 ,即
,即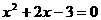 解这个方程,得
解这个方程,得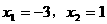 当
当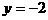 时,
时,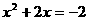 ,即
,即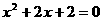
因为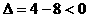 ,所以,这个方程没有实数根
,所以,这个方程没有实数根
经检验,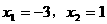 都是原方程的根。
都是原方程的根。
 原方程的根是
原方程的根是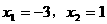
7.为了确保我市国家级卫生城市的称号,市里对主要街道的排污水沟进行改造. 其中光明施工队承包了一段要开挖96米长的排污水沟,开工后每天比原计划多挖2米,结果提前4天完成任务,问原计划每天挖多少米?
[解]设原计划每天挖x米,
由题意,得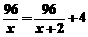
解之,得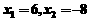
经检验,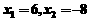 都是原方程的根,但工作效率为负数不合题意,
都是原方程的根,但工作效率为负数不合题意,
所以只取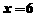
答:原计划每天挖6米.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com