
题目列表(包括答案和解析)
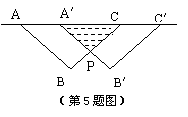
5. 如图,把等腰Rt△ABC沿AC方向平移到等腰Rt△A′B′C′的位置时,它们重叠的部分的面积是Rt△ABC面积的一半.若AB=2cm,则它移动的距离AA′= _cm;
4.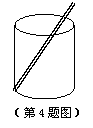
 如图,有一个透明的圆柱型形状的玻璃杯,由内部测得其底面半径为3cm,高为8cm.另有一支12cm长的吸管斜放于杯中.若不考虑吸管的粗细,则吸管露出杯中外部的长度最小为 cm;
如图,有一个透明的圆柱型形状的玻璃杯,由内部测得其底面半径为3cm,高为8cm.另有一支12cm长的吸管斜放于杯中.若不考虑吸管的粗细,则吸管露出杯中外部的长度最小为 cm;
3.矩形的长为acm,宽为5cm,把长减小2cm,宽增加2cm后,所得的矩形面积比原来矩形面积大 cm2;
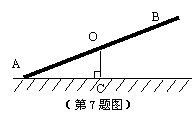
2.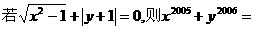 ;
;
1.我市某天早上气温是-60C中午上升了90,到了夜间又下降了120C,这天我市夜间的温度是 ;
28、(8分)如图:直线y=x-2与x轴、y轴分别交于点A、B,M(t,0)是x轴上异于A的一点,以M为圆心且过点A的圆记为⊙M.
(1)求证:直线AB将⊙M的周长分为1:3两部分;
(2)若直线AB被⊙M所截得的弦长为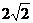 ,求t的值;
,求t的值;
(3)若点N是⊙M上的一点,是否存在实数t,使得四边形ABMN为平行四边形?若存在,求出t的值,并写出N的坐标;若不存在,说明理由.
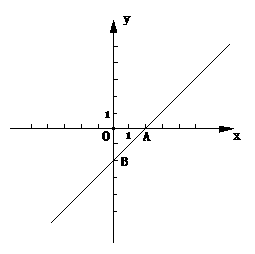

23.(15分)已知抛物线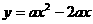 与直线
与直线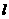 :
: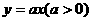 的交点除了原点
的交点除了原点 外,还相交于另一点
外,还相交于另一点 .
.
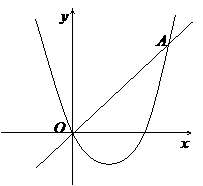 (1)分别求出这个抛物线的顶点、点
(1)分别求出这个抛物线的顶点、点 的坐标(可用含
的坐标(可用含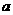 的式子表示);
的式子表示);
(2)将抛物线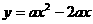 沿着
沿着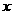 轴对折(翻转
轴对折(翻转 )后,得到的图象叫做“新抛物线”,则:
)后,得到的图象叫做“新抛物线”,则:
①当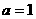 时,求这个“新抛物线”的解析式,并判断这个“新抛物线”的顶点是否在直线
时,求这个“新抛物线”的解析式,并判断这个“新抛物线”的顶点是否在直线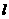 上;
上;
②在①的条件下,“新抛物线”上是否存在一点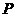 ,使点
,使点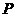 到直线
到直线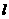 的距离等于线段
的距离等于线段 的
的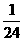 ?若存在,请直接写出满足条件的点
?若存在,请直接写出满足条件的点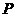 坐标;若不存在,请说明理由。
坐标;若不存在,请说明理由。
28、证明:(1)∵AE⊥BD,∴=,∴∠EBD=∠ECB.∵∠ABH=∠DBH,∠BHE=∠ECB+∠CBH,∠HBE=∠DBH+∠EBD,∴∠BHE=∠HBE. ∴BE=HE.
解: (2)连结QC、TB,则∠BCQ+∠CBQ=90°,又∠BDQ+∠ATD=90°,而∠BCQ=∠BDQ,∴∠CBQ=∠ATD=∠ATB,∴ΔABG∽ΔATB,∴AB2=AG•AT,∵AH⊥CE,∴H为CE的中点,∴BE=EC,∴ΔBEO∽ΔCBE,∴==. 设⊙A的半径为R,由AB2-OA2=BO2,OE=R-3,得R2-32=4(R-3)2,解得,R=5,或R=3(不合题意,舍去).∴AT•AG=AB2=25.
(方法二提示:可连结AD,CD证ΔBAG∽ΔTAD)
(3)答:②的值不变.
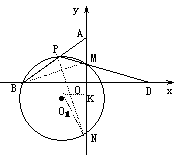 证明:作O1K⊥MN于K,连结O1N、PN、BM,
证明:作O1K⊥MN于K,连结O1N、PN、BM,
则MN=2NK, 且∠N O1K=∠NPM,
∴==2sin∠NO1K=2sin∠NPM,
由直线y=x+3 得 OB=OD=4,OM⊥BD,
∴∠BMO=∠DMO,
又∠BMO=∠ABM+∠BAM,∠DMO=∠MPN+∠PNM,
∵∠ABM=∠PNM,
∴∠MPN=∠BAM=∠NO1K,=2sin∠BAM=2×= ,
所以的值不变,其值为 .
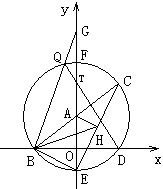
30、已知:如图1,直线y=kx+3(k>0)交x轴于点B,交y轴于点A,以A点为圆心,AB为半径作⊙A交x轴于另一点D,交y轴于点E、F两点,交直线AB于C点,连结BE、CF,∠CBD的平分线交CE于点H.
(1)求证:BE=HE;
(2)若AH⊥CE,Q为 上一点,连结DQ交y轴于T,连结BQ并延长交y轴于G,
求AT•AG的值;
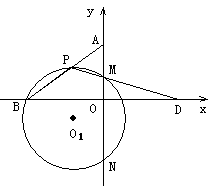
 (3)如图2, P为线段AB上一动点(不与A、B两点重合),连结PD交y轴于点M,过P、M、B三点作⊙O1交y轴于另一点N,设⊙O1的半径为R,当k=时,给出下列两个结论:①MN的长度不变;②的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
(3)如图2, P为线段AB上一动点(不与A、B两点重合),连结PD交y轴于点M,过P、M、B三点作⊙O1交y轴于另一点N,设⊙O1的半径为R,当k=时,给出下列两个结论:①MN的长度不变;②的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
28、解:(1)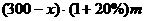 ,
, ,
,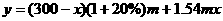
(2)由题意得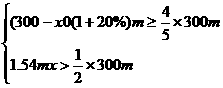
解得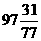 <
<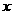 ≤100。注:写97.5<
≤100。注:写97.5<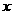 ≤100或97.4<
≤100或97.4<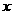 ≤100均视为正确
≤100均视为正确
∵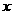 为整数 ∴
为整数 ∴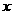 只能取98、99、100。
只能取98、99、100。
故共有三种调配方案:
①202人继续生产A种产品,调98人生产B种产品;
②201人继续生产A种产品,调99人生产B种产品;
③200人继续生产A种产品,调100人生产B种产品;
又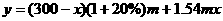 =
=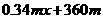 ,由于
,由于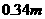 >0,函数
>0,函数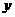 随
随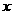 的增大而增大。故当
的增大而增大。故当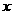 =100,即按第三种方案安排生产时,获总利润最大。
=100,即按第三种方案安排生产时,获总利润最大。
(3)当 =2时,最大总利润为788万元。根据题意,可投资开发产品F、H或C、D、E或C、D、G或C、F、G。
=2时,最大总利润为788万元。根据题意,可投资开发产品F、H或C、D、E或C、D、G或C、F、G。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com