
题目列表(包括答案和解析)
3.二次函数表达式
[例6]已知二次函数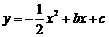 的图象经过点A(-3,-6),并与x轴交于点B(-1,0)和点C,顶点为P。
的图象经过点A(-3,-6),并与x轴交于点B(-1,0)和点C,顶点为P。
(1)求二次函数的解析式;
(2)设点D为线段OC上一点,且∠DPC=∠BAC,求点D的坐标;
说明:若(2)你经历反复探索没有获得解题思路,请你在不改变点D的位置的情况下添加一个条件解答此题,此时(2)最高得分为3分。
[例7已知抛物线y=x2-2x+m与x轴交于点A(x1,0)、B(x2,0)(x2>x1),
(1) 若点P(-1,2)在抛物线y=x2-2x+m上,求m的值;
(2)若抛物线y=ax2+bx+m与抛物线y=x2-2x+m关于y轴对称,点Q1(-2,q1)、Q2(-3,q2)都在抛物线y=ax2+bx+m上,则q1、q2的大小关系是
(请将结论写在横线上,不要写解答过程;友情提示:结论要填在答题卡相应的位置上)
(3)设抛物线y=x2-2x+m的顶点为M,若△AMB是直角三角形,求m的值.
2. 二次函数的图象及性质
二次函数的图象及性质
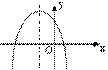
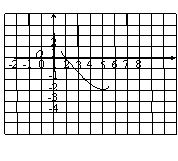
[例3] 已知二次函数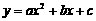 的图象如右图所示,则a、b、c满足( )
的图象如右图所示,则a、b、c满足( )
A、a<0,b<0,c>0 B、a<0,b<0, c<0
 C、a<0,b>0,c>0 D、 a>0,b<0,c>0
C、a<0,b>0,c>0 D、 a>0,b<0,c>0
[例4]二次函数y=x2的图象向上平移2个单位,得到新的图象的二次函数表达式是( )
A、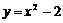 B、
B、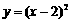
C、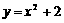 D、
D、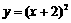
[例5]已知抛物线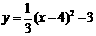 的部分图象(如图),图象再次与x轴相交时的坐标是( )
的部分图象(如图),图象再次与x轴相交时的坐标是( )
A、(5,0) B、(6,0)
C、(7,0) D、(8,0)
1.二次函数的对称轴及顶点
[例1] 二次函数y=x2-2x+1的对称轴方程是x=_______.
[例2] 已知抛物线的解析式为y=(x-2)2+1,则抛物线的顶点坐标是( )
A、(-2,1) B、(2,1) C、(2,-1) D、(1,2)
12.抛物线y=ax2+(b-1)x+2.
(1)若抛物线经过点(1,4)、(-1,-2), 求此抛物线的解析式;
(2) 若此抛物线与直线y=x有两个不同的交点P、Q,且点P、Q关于原点对称.
① 求b的值;
② 请在横线上填上一个符合条件的a的值: a = ,并在此条件下画出该函数的图象.
(15)二次函数
考试内容]
二次函数及其图象,一元二次方程的近似解.
[考试要求]
①通过对实际问题情境的分析确定二次函数的表达式,并体会二次函数的意义.
②会用描点法画出二次函数的图象,能从图象上认识二次函数的性质.
③会根据公式确定图象的顶点、开口方向和对称轴(公式不要求推导和记忆),并能解决简单的实际问题.
④会利用二次函数的图象求一元二次方程的近似解.
[考点复习]
11.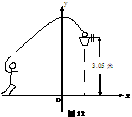 如图12,一位篮球运动员跳起投篮,球沿抛物线
如图12,一位篮球运动员跳起投篮,球沿抛物线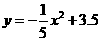 运行,然后准确落入篮框内.已知篮框的中心离地面的距离为3.05米.
运行,然后准确落入篮框内.已知篮框的中心离地面的距离为3.05米.
(1)球在空中运行的最大高度为多少米?
(2)如果该运动员跳投时,球出手离地面的高度为2.25米,请问他距离篮框中心的水平距离是多少?
10.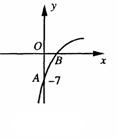 已知抛物线
已知抛物线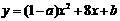 的图象的一部分如图所示,抛物线的顶点在第一象限,且经过点A(0,-7)和点B.
的图象的一部分如图所示,抛物线的顶点在第一象限,且经过点A(0,-7)和点B.
(1)求a的取值范围;
(2)若OA=2OB,求抛物线的解析式.
9.某产品每件成本10元, 试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
8. 已知二次函数
已知二次函数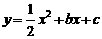 的图象经过点A(C,-2),
的图象经过点A(C,-2),
求证:这个二次函数图象的对称轴是x=3.
题目中的矩形框部分是一段被墨水染污了无法辩认的文字.
(1)根据已知和结论中现有的信息,你能否求出题中的二次函数解析式?若能,请写出求解过程,并画出二次函数的图象;若不能,请说明理由.
(2)请你根据已有的信息,在原题中的矩形框中,填加一个适当的条件,把原题补充完整.
7.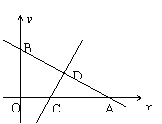 如图,一次函数
如图,一次函数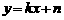 的图象与x轴和y轴分别交于点A(6,0)和B(0,
的图象与x轴和y轴分别交于点A(6,0)和B(0,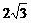 ),线段AB的垂直平分线交x轴于点C,交AB于点D.
),线段AB的垂直平分线交x轴于点C,交AB于点D.
(1)试确定这个一次函数关系式;
(2)求过A、B、C三点的抛物线的函数关系式.
6.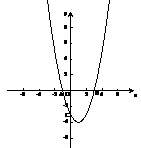 在直角坐标平面中,O为坐标原点,二次函数
在直角坐标平面中,O为坐标原点,二次函数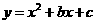 的图象与x轴的负半轴相交于点C(如图5),点C的坐标为(0,-3),且BO=CO
的图象与x轴的负半轴相交于点C(如图5),点C的坐标为(0,-3),且BO=CO
(1)求这个二次函数的解析式;
(2)设这个二次函数的图象的顶点为M,求AM的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com