
题目列表(包括答案和解析)
1、 如图19-1,正方形A的面积是16,正方形的面积B为9,那么正方形C的面积为_______
27、(12分) 如图19-12。公路AB和铁路CD在点P处交汇,且∠BPD=600,点Q在∠BPD的平分线上,且在Q点处有一疗养院,PQ=240米,设大型运输车在行驶时。110米范围内都会受到噪声影响,火车在铁路上行驶时,周围200米以内都受噪声影响。
① 当大型运输车和火车分别沿PB、PD方向行驶时,疗养院是否会受到噪声的影响?请你与同学交流说明理由。
② 如果受到影响,已知大型运输车的平均速度为60千米/小时,火车的平均速度为90千米/小时,那么疗养院影响的时间为多少秒?
③ 如果公路AB上大型运输车的通过率为10辆/小时,铁路CD上火车的通车率为5列/小时,请你计算一下该疗养院是否应该搬迁,并说明理由。
第25部分《解直角三角形》综合测试题B
 
A C  B 图19-1 |
26、(10分) 细心观察图形,认真分析各式,然后解答问题:
             1 A6   1 A5
1 A5S6 S5 1 A4 S4 1A3 S3 1 S2 A2  S1
A1
S1
A1
O 图19-11 |
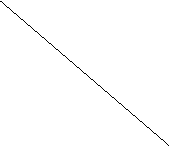
(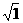 )2+1=2,S1=
)2+1=2,S1=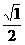 ;
;
(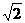 )2+1=3,S2=
)2+1=3,S2=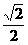 ;
;
(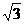 )2+1=4,S3=
)2+1=4,S3=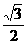 ;
;
…… ……
① 请用含有n(n为正整数)的等式表示上述变化规律;
② 推算出OA10的长
③ 求出S12+ S22+ S32+…+ S102的值。
      C
B C
B Q
QP A D 图19-12 |
25、(10分) (参考数据:sin650≈0.9,cos650≈0.4,tan650≈2.1,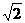 ≈1.4) 如图19-10,某海滨浴场岸边可近似地看成直线,位于岸边A处的救生员发现海中B处有人求救,1号救生员没有直接从A处游向B处,而是在岸边自A处跑300米到距离B最近的D处,然后游向B
≈1.4) 如图19-10,某海滨浴场岸边可近似地看成直线,位于岸边A处的救生员发现海中B处有人求救,1号救生员没有直接从A处游向B处,而是在岸边自A处跑300米到距离B最近的D处,然后游向B
   B B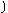  450 650 450 650

A C D海岸 图19-10 |
 处;假定所有的救生员在岸边的跑行的速度这6米/秒,在海中游进的速度为2米/秒,∠BAD=450。
处;假定所有的救生员在岸边的跑行的速度这6米/秒,在海中游进的速度为2米/秒,∠BAD=450。
① 请根据以上条件分析1号救生员的选择是否正确;
② 若2号救生员同时从A处在岸边跑到C处,再游向B处,已知∠BCD=650,问哪位救生员先赶到B处救人?(为了便于计算,计算过程中的数值均可精确到0.1)。
24、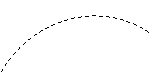 (6分)如图19-9,设火柴盒ABCD的两边之长为a和b,对角线长为c,推倒后的火柴盒是AB/C/D/,试用该图形验证勾股定理的正确性。
(6分)如图19-9,设火柴盒ABCD的两边之长为a和b,对角线长为c,推倒后的火柴盒是AB/C/D/,试用该图形验证勾股定理的正确性。
23、(8分)如图19-8,D是△ABC的边AC上一点,CD=2AD,AE⊥BC,交BC于点E,若BD=8,sin∠CBD=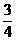 求AE的长。
求AE的长。
   D
C D
C  C/
B/ C/
B/a c c b D/ b A a B 图19-9 |
22、如图19-7是一块长宽高分别为6cm、4cm和3cm的长方体木块,一只蚂蚁要从长方体木块的一个顶点A处沿着长方体的表面到长方体上和A点相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )
A.(3+2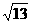 )cm B.
)cm B.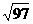 cm C.
cm C. 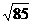 cm D.9 cm
cm D.9 cm
21、如图19-6,两建筑物的水平距离为a m,从A点测得C点的俯角为α,测得D点的俯角为β,则较低建筑物CD的高为( )
A. a m B.atanα m C. a cotαm D. a(tanβ-tanα)m
     A
AD
B E C 图19-8 |
20、如图19-5,Rt△ABC中,∠C=900,D为BC上一点,
∠DAC=300,BD=2,AB=2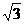 ,则AC的长是(
)
,则AC的长是(
)
A. 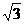 B.2
B.2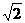 C. 3 D.
C. 3 D.
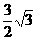
      A A   α αβ C B D 图19-6 |
  A A
C D B 图19-5 |
    B B3 4 A 6 图19-7 |
19、如图19-4,Rt△ABC中,∠ACB=900,CD⊥AB于D,BC=3,AC=4,设∠BCD=α,则tanα的值为( )
A.
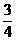 B.
B.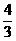 C.
C.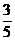 D.
D. 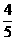
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com