
题目列表(包括答案和解析)
17.已知函数y=x-5,令x=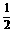 、1、
、1、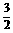 、2、
、2、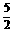 、3、
、3、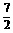 、4、
、4、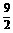 、5,可得函数图象上的十个点.在这十个点中随机取两个点P(x1,y1)、Q(x2,y2),则P、Q两点在同一反比例函数图象上的概率是( B )
、5,可得函数图象上的十个点.在这十个点中随机取两个点P(x1,y1)、Q(x2,y2),则P、Q两点在同一反比例函数图象上的概率是( B )
(A)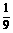 (B)
(B)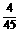 (C)
(C)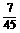 (D)
(D)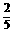
16.有2名男生和2名女生,王老师要随机地、两两一对地为他们排座位,一男一女排在一起的概率是( ) D
(A) (B) (C) (D)
15.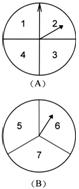 甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示. 游戏规定,转动两个转盘停止后,指针所指的两个数字之和为奇数时,甲获胜;为偶数时,乙获胜.
甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示. 游戏规定,转动两个转盘停止后,指针所指的两个数字之和为奇数时,甲获胜;为偶数时,乙获胜.
(1)用列表法(或画树状图)求甲获胜的概率;
(2)你认为这个游戏规则对双方公平吗?请简要说明理由.
解:⑴(法1)画树状图
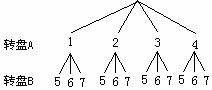
由上图可知,所有等可能的结果共有12种,指针所指的两个数字之和为奇数的结
果有6种. ∴P(和为奇数)=0.5
 (法2)列表如下:
(法2)列表如下:

|
1 |
2 |
3 |
4 |
||||||||||||||
|
5 |
1+5=6 |
2+5=7 |
3+5=8 |
4+5=9 |
||||||||||||||
|
6 |
1+6=7 |
2+6=8 |
3+6=9 |
4+6=10 |
||||||||||||||
|
7 |
1+7=8 |
2+7=9 |
3+7=10 |
4+7=11 |
由上表可知,所有等可能的结果共有12种,指针所指的两个数字之和为奇数的结
果有6种. ∴P(和为奇数)=0.5
⑵∵P(和为奇数)=0.5
∴P(和为偶数)=0.5
∴这个游戏规则对双方是公平的.
14.在一个不透明的箱子里放有除颜色外,其余都相同的4个小球,其中红球3个、白球1个.搅匀后,从中同时摸出2个小球,请你写出这个实验中的一个可能事件: . 例如:“摸出2个红球”;
13. 王强与李刚两位同学在学习“概率”时.做抛骰子(均匀正方体形状)实验,他们共抛了54次,出现向上点数的次数如下表:
|
向上点数 |
1 |
2 |
3 |
4 |
5 |
6 |
|
出现次数 |
6 |
9 |
5 |
8 |
16 |
10 |
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率.
(2)王强说:“根据实验,一次试验中出现向上点数为5的概率最大.”
李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”
请判断王强和李刚说法的对错.
(3)如果王强与李刚各抛一枚骰子.求出现向上点数之和为3的倍数的概率.
.(1)出现向上点数为3的频率为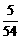 ,出现向上点数为5的频率为
,出现向上点数为5的频率为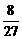
(2)都错
(3)画树状图或列表或简单说理(正确),概率P=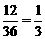 .
.
12、(1)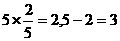 答:袋中有2个红球,3个白球. (2)
答:袋中有2个红球,3个白球. (2)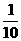
11.袋中共有5个大小相同的红球、白球,任意摸出一球为红球的概率是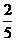 .
.
(1)袋中红球、白球各有几个?
(2)任意摸出两个球均为红球的概率是_________________.
10.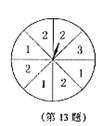 晓明玩转盘游戏,当他转动如图所示的转盘,转盘停止时指针指向2的概率是_________.
晓明玩转盘游戏,当他转动如图所示的转盘,转盘停止时指针指向2的概率是_________.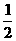 (或0.5,50%)
(或0.5,50%)
9.某商场在“五一”期间推出购物摸奖活动,摸奖箱内有除颜色以外完全相同的红色、白色乒乓球各两个.顾客摸奖时,一次摸出两个球,如果两个球的颜色相同就得奖,颜色不同则不得奖.那么顾客摸奖一次,得奖的概率是 .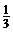
8.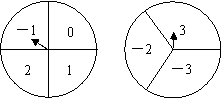 (1)如图所示的转盘中指针落在每个数字上的机会相等,现同时转动A、B两转盘,停止后,指针各指向一个数字.小彬和小颖利用这个转盘做游戏:若两数之积为非负数则小彬胜,否则,小颖胜.你认为这个游戏对双方公平吗? .(直接写出结果)
(1)如图所示的转盘中指针落在每个数字上的机会相等,现同时转动A、B两转盘,停止后,指针各指向一个数字.小彬和小颖利用这个转盘做游戏:若两数之积为非负数则小彬胜,否则,小颖胜.你认为这个游戏对双方公平吗? .(直接写出结果)
不公平,因为共有12个积,而其中的非负数有7个,
故P(小彬胜)=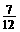 ,P(小颖胜)=
,P(小颖胜)=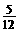 ,
,
P(小彬胜)>P(小颖胜),所以不公平.
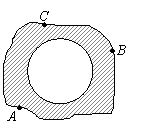 (2)小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,小明在封闭图形内划出了一个半径为1米的圆,在不远处向圈内掷石子,且记录如下:
(2)小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,小明在封闭图形内划出了一个半径为1米的圆,在不远处向圈内掷石子,且记录如下:
 |
50次 |
150次 |
300次 |
|
石子落在⊙O内(含⊙O上)的次数m |
14 |
43 |
93 |
|
石子落在阴影内的次数n |
19 |
85 |
186 |
你能否求出封闭图形ABC的面积?试试看.
由表可知,P(石子落在⊙O内)=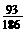 =0.5,故可估计S⊙O: S封闭图形ABC=0.5,因为S⊙O=
=0.5,故可估计S⊙O: S封闭图形ABC=0.5,因为S⊙O=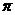 ,
,
所以S封闭图形ABC=2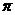 (m2).
(m2).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com