
题目列表(包括答案和解析)
2.方程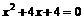 的根的情况是(
)
的根的情况是(
)
(A)有两个不相等的实数根 (B)有两个相等的实数根
(C)有一个实数根 (D)没有实数根
1.点P(-1,4)关于x轴对称的点P′的坐标是( )
(A)(-1,-4) (B)(-1,4)
(C)(1,-4) (D)(1,4)
29、(1)连结DB,则∠DBO=90°
∵AB切⊙O于点C∵.AB⊥OD,又OD是⊙O’直径,即OA=OB
得OA2=OC·OD=r·2R=2Rr.即OA·OB=2rR
(也可证明△OBD∽△OCA)
(2)无变化 连结00',并延长交⊙O'于D点,连结DB、OC.
证明△OCA∽△OBD,得OA·OB=OC·OD=r·2R=2Rr
(3)无变化 连结00’,并延长交⊙O’于B点,连结DB、OC
证出△OCA∽△OBD,得OA·OB=OC·OD.:r·2R=2Rr
28、略。
27、 1,4,10,……
|
点的个数 |
可连成三角形个数 |
|
3 |
1=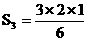 |
|
4 |
4=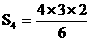 |
|
5 |
10=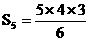 |
|
…… |
…… |
|
n |
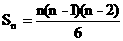 |
推理:平面上有n个点,过不在同一条直线上的三个点可以确定一个三角形,取第一个点A有n种方法,取第二个点有B有(n-1)种取法,取第三个点C有(n-2)种取法,所以一共可以作n(n-1)(n-2)个三角形,但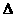 ABC、
ABC、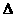 ACB、
ACB、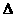 BAC、
BAC、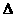 BCA、
BCA、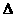 CAB、
CAB、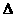 CBA是同一个三角形,故应除以6,即
CBA是同一个三角形,故应除以6,即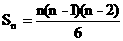 。
。
结论: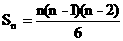
26、(1)∠CEB=∠FDC
(2)每画-个图正确得1分
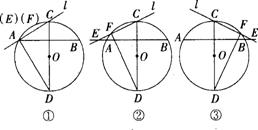
(注:3个图中只需画两个图)
证明:。如图②
∵ CD是⊙O的直径,点C是AB的中点,
∴ CD⊥AB,∴ ∠CEB+∠ECD=90°
∵ CD是⊙O的直径,.∴ ∠CFD=90°
∴ ∠FDC+∠ECD=90°∴ ∠CEB=∠FDC
25、(1)直线L1 yl=O.03x+2(0≤x≤2000)
设直线L2的解析式为y2=0.012x+20(0≤x≤2000)
(2)当yl=y2时,两种灯的费用相等 0.03X+2=0.012X+20
解得:x=1000
∴ 当照明时间为1000小时时,两种灯的费用相等
(3)节能灯使用2000小时,白炽灯使用500小时
24、(1)小明的结果不对
设小路宽xm,则得方程(16-2x)(12-2x)=16×12/2解得:x1=2.x2=12
而荒地的宽为12m,若小路宽为12m,不符合实际情况,故x2=12m不合题意
(2)由题意得:4×πx2/4=16×12/2
x2=96/π x≈5.5m
答:小颖的设计方案中扇形的半径约为5.5m.
(3)


22、m=-3,舍去m=1; 23、BE=2;
18、-23; 19、2; 20、b;
21、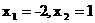 (增根)
(增根)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com