
题目列表(包括答案和解析)
2、抛物线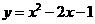 的顶点坐标是( )
的顶点坐标是( )
A、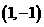 B、
B、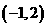 C、
C、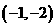 D、
D、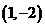
1、抛物线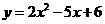 的对称轴是( )
的对称轴是( )
A、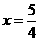 B、
B、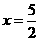 C、
C、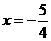 D、
D、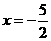
24.(本题满分11分)
解:⑴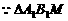 ∽
∽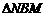 ,且
,且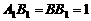 ,
,
∴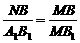 ,………………………………………………………2分
,………………………………………………………2分
即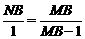 ,
,
整理,得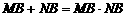 ,两边同除以MB·NB得,
,两边同除以MB·NB得,
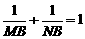 .…………………………………………………………4分
.…………………………………………………………4分
⑵由题意,得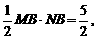 即
即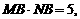 又由⑴可知
又由⑴可知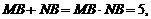 ………………………………………………5分
………………………………………………5分
∴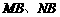 分别是方程
分别是方程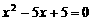 的两个实数根.…………………6分
的两个实数根.…………………6分
解方程,得
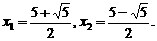 …………………………………………………7分
…………………………………………………7分
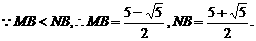 ………………………………8分
………………………………8分
⑶由⑵知,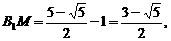
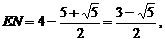 ……9分
……9分
∵图 ②中的BN与图①中的EN相等,
∴BN=B1M,………………………………………………………………10分
∴四边形BB1MN是矩形,∴MN的长是1.………………………………11分
注意:考生若给出其它解法,应参考本标准给出相应的分数.
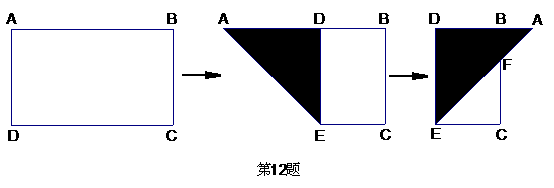
12.如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF的面积为( )
A.4 B.6 C.8 D.10
10、用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案:
(1)第四个图案中有白色地砖 块;
(2)第 个图案中有白色地砖
块;
个图案中有白色地砖
块;
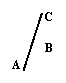
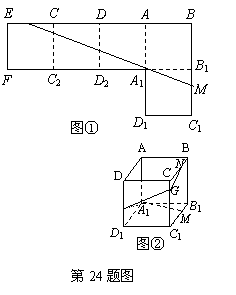 图①是由五个边长都是1的正方形纸片拼接而成的,过点A1的直线分别与BC1、BE交于点M、N,MN与CC2交于点G,且图①被直线MN分成面积相等的上、下两部分.
图①是由五个边长都是1的正方形纸片拼接而成的,过点A1的直线分别与BC1、BE交于点M、N,MN与CC2交于点G,且图①被直线MN分成面积相等的上、下两部分.
⑴求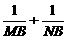 的值;
的值;
⑵求MB、NB的长;
⑶将图①沿虚线折成一个无盖的正方体纸盒(图②)后,求两点M、N间的距离.
18.观察下列顺序排列的等式:
9×0+1=1,
9×1+2=11,
9×2+3=21,
9×3+4=31,
9×4+5=41,
…… .
猜想:第n个等式(n为正整数)应为____________________________.
20.如图,由边长为1的25个小正方形组成的正方形网
格上有一个△ABC;在网格上画出一个与△ABC相似
且面积最大的△A1B1C1,使它的三个顶点都落在小正
方形的顶点上,则△A1B1C1的最大面积是__________.
3.现有四个有理数3,4,-6,10。将这四个数(每个数用且只用一次)进行加、减、乘、
除四则运算,使其结果等于24,其三种本质不同的运算式如下:
(1)__________(2)___________(3)_________
另有四个数3,-5,7,-13,可通过运算式(4)_____________使其结果等于24。
几个不等于零的数相乘,积的符号由负因数的个数决定。
例如,考察代数式(x-1)(x-2)的值:
当x<1时,x-1<0,x-2<0.∴(x-1)( x-2)>0;
当1<x<2时,x-1>0, x-2<0,∴(x-1)( x-2)<0;
当x>2时,x-1>0,x-2>0,∴(x-1)( x-2)>0;
∴当x<1或x>2时,(x-1)( x-2)>0;
当1<x<2时,(x-1)( x-2)<0;
(2)填写下表:(用“+”或“-”填入空格)
  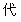 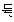 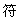 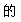  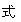 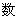 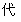  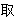 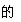 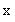 |
x<-2 |
-2<x<-1 |
-1<x<3 |
3<x<4 |
4<x<5 |
x>5 |
|
x+2 |
- |
+ |
+ |
+ |
+ |
+ |
|
x+1 |
- |
|
+ |
+ |
+ |
+ |
|
x-3 |
- |
- |
|
+ |
+ |
+ |
|
x-4 |
- |
- |
- |
|
|
+ |
|
x-5 |
- |
- |
- |
- |
- |
+ |
|
(x+2)(x+1)(x-3)(x-4)(x-5) |
- |
|
|
+ |
|
+ |
(3)根据以上填表,写出当x__________________时,
(x+2)(x+1)(x-3)(x-4)(x-5)<0
请你运用所发现的规律,写出当x___________________________时,
(x-8)(x-9)(x-10)(x-11)>0
10. (扬州)计算机是将信息转换成二进制数进行处理的,二进制即“逢2进1”,如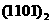 表示二进制数,将它转换成十进制形式是
表示二进制数,将它转换成十进制形式是
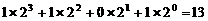 ,那么将二进制数
,那么将二进制数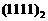 转换成十进制形式是数
转换成十进制形式是数
A、8 B、15 C、20 D、30
9.(河南)观察下面一列数的规律并填空:0,3,8,15,24,…,则它的第2002个数是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com