
题目列表(包括答案和解析)
15.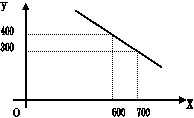 某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量Y(件)与销售单价X(元/件)可近似看作一次函数y=kx+b的关系(如图)。
某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量Y(件)与销售单价X(元/件)可近似看作一次函数y=kx+b的关系(如图)。
(1) 根据图象,求出一次函数的解析式;
(2) 设公司获得的毛利润(毛利润=销售总价-成本总价)为S元。
① 试用销售单价X表示毛利润S;
② 请结合S与X的函数图象说明:销售单价定为多少时,该公司可获得最大利润?最大利润是多少?此时销售量是多少?
14.某服装经销商甲,库存有进价每套400元的A品牌服装1200套,正常销售时每套600元,每月可卖出100套,一年内刚好卖完,南在市场流行B品牌服装,此品牌服装进价每套200元,售出价每套500元,每月可卖出120套(两种服装的市场行情互不受影响)。目前有一可进B品牌服装的机会,若这一机会错过,估计一年内也不能进到这种服装,可是经销商甲手头又无流动资金可用,只有低价转让A品牌服装,经与经销商乙协商,达成协议,转让价格(元/套)与转让数量(套)有如下关系:
|
转让数量(套) |
1200 |
1100 |
1000 |
900 |
800 |
700 |
600 |
500 |
400 |
300 |
200 |
100 |
|
价格(元/套) |
240 |
250 |
260 |
270 |
280 |
290 |
300 |
310 |
320 |
330 |
340 |
350 |
现在经销商甲面临三种选择:
方案1:不转让A品牌,也不转让B品牌;
方案2:全部转让A品牌,用转让来的资金购B品牌后,经销B品牌;
方案3:部分转让A品牌,用转让来的资金购B品牌后,经销B品牌,同时也经销A品牌。问:
(1) 销商甲选择方案1与方案2一年内分别获得利润多少元?
(2) 经销商甲选择哪种方案可以使自己在一年内获得最多利润?若选用方案3,请问他转让给经销商乙的A种品牌的数量是多少(精确到百套)?此时,他在这一年内共得利润多少元?
13.有一种螃蟹,从海上捕获后不放养最多只能活两天,如果放养在塘内,可以延长存活时间,但每天也有一定数量的蟹死去,假设放养期内蟹的个体重量基本保持不变,现有一经销商,按市场价收购了这种活蟹1000千克放养在塘内,此时市场价为每千克30元,据测算,以后每千克活蟹的市场价每天可上升1元,但是放养一天需各种费用支出400元,且平均每天还有10千克蟹死去,假定死蟹均于当天全部售出,售价都是每千克20元。
(1) 设X天后每千克活蟹的市场价为P元,写出P关于X的函数关系式。
(2) 如果放养X天后将活蟹一次性出售,并记1000千克蟹的销售额为Q元,写出Q关于X的函数关系式。
(3) 该经销商将这批蟹放养多少天后出售,可获最大利润(利润=销售总额-收购成本-费用),最大利润是多少?
12.某公司生产的A种产品,它的成本是2元,售价是3元,年销售为100万件,为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元时,产品的年销售量将是原销售量的y倍,且y是x的二次函数,它们的关系如表所示:
(1)求y与x的函数的关系式;
(2)如果把利润看作是销售总额减去成本费和广告费,试写出年利润S(十万元)和x(十万元)的函数关系式?
(3)如果投入的年广告费为10万至30万元,问广告费在范围内,公司获得的年利润随广告费的增大而增大?
11.某商店购进一批单价为16元的日用品,销售一段时间后,为了获得更多的利润,商店决定提高销售价格。经检验发现,若按每件20元的价格销售时,每月能卖360件若按每件25元的价格销售时,每月能卖210件。假定每月销售件数y(件)是价格X的一次函数.
(1) 试求Y与X的之间的关系式.
(2) 在商品不积压,且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润,每月的最大利润是多少?(总利润=总收入-总成本)
|
x(十万元) |
0 |
1 |
2 |
…… |
|
y |
1 |
1.5 |
1.8 |
······ |
10.某商场以每件30元的价格购进一种商品,试销中发现,这种商品每天的销量m(件)与每件的销售价x(元)满足一次函数:m=162-3x.
(1) 写出商场卖这种商品每天的销售利润y与每件的销售价x间的函数关系式;
(2) 如果商场要想每天获得最大销售利润,每件商品的定价为多少最合适?最大销售利润为多少?
9.如图4,有一块铁皮,拱形边缘呈抛物线状,MN=4dm,抛物线顶点处到边MN的距离是4dm,要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在边MN上,A、D落在抛物线上,问这样截下去的矩形铁皮的周长能否等于8dm?
8.某化工材料经销公司购进了一种化工原料共7000千克,购进价格为每千克30元。物价部门规定其销售单价不得高于每千克70元,也不得低于30元。市场调查发现:单价定为70元时,日均销售60千克;单价每降低1元,日均多售出2千克。在销售过程中,每天还要支出其它费用500元(天数不足一天时,按整天计算)。设销售单价为x元,日均获利为y元。
 (1)求y关于x的二次函数关系式,并注明x的取值范围;
(1)求y关于x的二次函数关系式,并注明x的取值范围;
(2)将(1)中所求出的二次函数配方成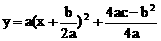 的形式,写出顶点坐标;在图2所示的坐标系中画出草图;观察图象,指出单价定为多少元时日均获得最多,是多少?
的形式,写出顶点坐标;在图2所示的坐标系中画出草图;观察图象,指出单价定为多少元时日均获得最多,是多少?
(3)若将这种化工原料全部售出,比较日均获利最多和销售单价最高这两种销售方式,哪一种获总利较多,多多少?
7.枇杷是莆田名果之一,某果园有100棵枇杷树。每棵平均产量为40千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵数接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量0.25千克,问:增种多少棵枇杷树,投产后可以使果园枇杷的总产量最多?最多总产量是多少千克?
注:抛物线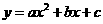 的顶点坐标是
的顶点坐标是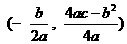
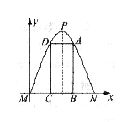
6.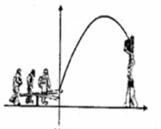 杂技团进行杂技表演,演员从跷跷板右端
杂技团进行杂技表演,演员从跷跷板右端 处弹跳到人梯顶端椅子
处弹跳到人梯顶端椅子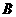 处,其身体(看成一点)的路线是抛物线
处,其身体(看成一点)的路线是抛物线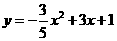 的一部分,如图.
的一部分,如图.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高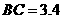 米,在一次表演中,人梯到起跳点
米,在一次表演中,人梯到起跳点 的水平距离是4米,问这次表演是否成功?请说明理由.
的水平距离是4米,问这次表演是否成功?请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com