
题目列表(包括答案和解析)
5、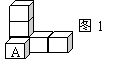 如图1是由六个边长为1个单位的小正方体搭成的几何体。小立方体A沿着它所在的水平线上以每秒1个单位移动,在它的移动过程中,不改变几何体的( )
如图1是由六个边长为1个单位的小正方体搭成的几何体。小立方体A沿着它所在的水平线上以每秒1个单位移动,在它的移动过程中,不改变几何体的( )
A、主视图 B、俯视图 C、左视图 D、三种视图
4、抛物线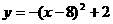 的顶点坐标是( )
的顶点坐标是( )
A、(2,8) B、(8,2) C、(-8,2) D、(-8,-2)
3.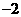 的倒数为( )
的倒数为( )
A.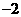 B.
B.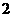 C.
C.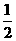 D.
D.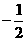
2.下列说法正确的是( )
A.9的平方根是3. B.将点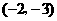 向右平移5个单位长度到点
向右平移5个单位长度到点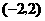
C.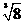 是无理数
D.点
是无理数
D.点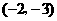 关于
关于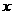 轴的对称点是
轴的对称点是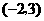
1、“神舟七号”宇航员翟志刚把足迹留在了茫茫太空,令国人深感自豪,他身穿的舱外航天服造价3000万元,用科学记数法表示3000万元为( )元
A、3×103 B、0.3×108 C、3×107 D、3×108
24.(本题14分)如图平面直角坐标系中,抛物线y=-x2+x+2 交x轴于A、B两点,交y轴于点C.
(1)求证:△ABC为直角三角形;
(2)直线x=m(0<m<4)在线段OB上移动,交x轴于点D,交抛物线于点E,交BC于点F.
求当m为何值时,EF=DF?
(3)连接CE和BE后,对于问题“是否存在这样的点E,使△BCE的面积最大?”
小红同学认为:“当E为抛物线的顶点时,△BCE的面积最大.”
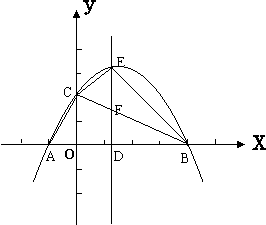 她的观点是否正确?提出你的见解,若△BCE的面积存在最大值,请求出点E的坐标和△BCE的最大面积.
她的观点是否正确?提出你的见解,若△BCE的面积存在最大值,请求出点E的坐标和△BCE的最大面积.
23、(本题12分)衢江区某一草莓种植大户,需将一批草莓运往省内各地,运输可选用两种汽车中的一种,都可在同一地点将这批草莓装上车沿同一条公路运往目的地。在运输过程中的有关数据如下:
 项目 项目运输工具 |
装卸 时间 (小时) |
装卸费用 (元) |
途中平均速度(千米/时) |
途中平均费用(元/千米) |
|
汽车A |
2 |
1100 |
80 |
8 |
|
汽车B |
3 |
1500 |
100 |
7 |
⑴设途中运输路程为x千米,用x表示汽车A比汽车B在途中多行驶的时间;
⑵若这批草莓在运输过程(包括装卸时间)中,损耗为160元/时,分别写出两种汽车在运输过程中所需的总费用yA(元)、yB(元)关于途中运输路程x(千米)的函数关系式;
⑶如果从节省费用的角度考虑,你认为采用哪种汽车较好?
22.(本题12分)在边长为1的正方形网格中,有形如帆船的图案①和半径为2的⊙P.
⑴将图案①进行平移,使A点平移到点E,画出平移后的图案;
⑵以点M为位似中心,在网格中将图案①放大2倍,画出放大后的图案,并在放大后的图案中标出线段AB的对应线段CD;
⑶在⑵所画的图案中,线段CD被⊙P所截得的弦长为 .(结果保留根号)

21.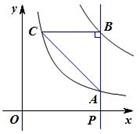 (本题10)如图,P为
(本题10)如图,P为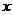 轴正半轴上一点,过点P作
轴正半轴上一点,过点P作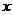 轴的垂线,交函数
轴的垂线,交函数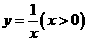 的图象于点A,交函数
的图象于点A,交函数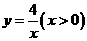 的图象于点B,过点B作
的图象于点B,过点B作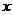 轴的平行线,交
轴的平行线,交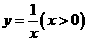 于点C,连结AC.
于点C,连结AC.
(1)当点P的坐标为(2,0)时,求△ABC的面积.
(2)当点P的坐标为(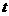 ,0)时,△ABC的面积是否随
,0)时,△ABC的面积是否随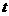 值的变化而变化?
值的变化而变化?
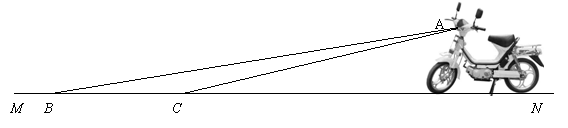
20.(本题8分)某厂家新开发的一种摩托车如图所示,它的大灯A射出的光线AB、AC与地面MN的夹角分别为8°和10°,大灯A离地面距离1 m.
(1)该车大灯照亮地面的宽度BC约是多少?(不考虑其它因素)
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2 s,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以60 km/h的速度驾驶该车,从60 km/h到摩托车停止的刹车距离是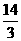 m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.
m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.
 (参考数据:
(参考数据: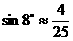 ,
,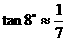 ,
,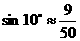 ,
,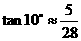 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com