
题目列表(包括答案和解析)
在证明几何定值题时,通常把题中变动的元素变到特殊位置。
例5. 设a为等边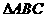 的边长,EF分别为AC、AB上的点,且满足
的边长,EF分别为AC、AB上的点,且满足 ,BE与CF交于点P,求证:
,BE与CF交于点P,求证: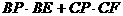 恒为一定值。
恒为一定值。
分析:如图3所示,设E和点C重合,那么F与点C重合,则点P与点C边重合,
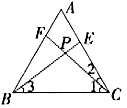 图3
图3
于是
证明:易证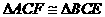
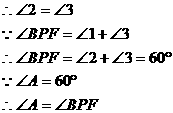
A、F、P、E四点共圆
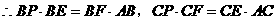
又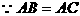
故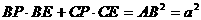 (定值)
(定值)
数形结合是把抽象的“数”转化为直观的“形”的数助形的思维转化方法。
例4. 如果正实数a,b,c,d满足
(1)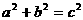 (2)
(2)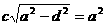
求证: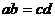
分析:若按常规法,由(1)(2)分别去求a、b、c、d则较繁,若构造几何图形来解,则较简便。
解:由(1)得到启示,可构造直角三角形ABC,如图2示,使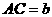 ,
,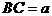 ,
,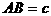
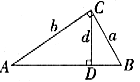
图2
由条件(2)可联想到射影定理,作斜边AB上的高CD,知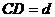 ,于是,由三角形面积公式,
,于是,由三角形面积公式,
得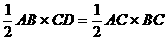
故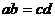
逆向思维是从事物的相反角度观察,探索克服学生思维过程中的单向思维定势,创造性地运用知识使问题化难为易。
例3. 如果m、n是互不相等的实数,并且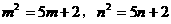 ,求
,求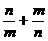 的值。
的值。
分析:若先求出m、n的值,再求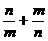 的值,则较繁,如果逆向运用方程的根定义,把m、n看成方程
的值,则较繁,如果逆向运用方程的根定义,把m、n看成方程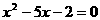 的两根,由韦达定理知;
的两根,由韦达定理知;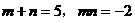 ,于是有
,于是有
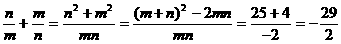
对一些问题,不能“一叶障目”,而要通过研究问题的整体形式和结构,进行整体处理,则可达到速解题目的目的。
例2. 已知直角三角形的周长为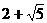 ,斜边上的中线为1,求直角三角形的面积。
,斜边上的中线为1,求直角三角形的面积。
分析:如图1,设两直角边分别各a,b,则
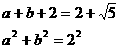
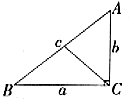 图1
图1
若分别解出a、b,然后再求直角三角形面积,则较繁,若视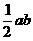 为一整体来求,则简便得多。
为一整体来求,则简便得多。
解:由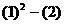 得
得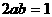
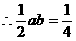 ,即直角三角形的面积为
,即直角三角形的面积为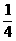
遇到复杂的问题,可透过问题的本质将其分解成简单的小问题逐一去解决。
例1. 如果三个方程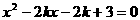 ,
,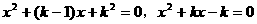 中,至少有一个方程有实根,求k的取值范围。
中,至少有一个方程有实根,求k的取值范围。
分析:如果从总体考虑方程有实根的情况,则较繁;若用分解思维进行转化,则较简便。
解:设三个方程都没有实数根
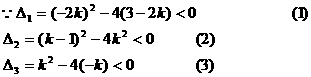
由(1)得: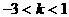
由(2)得: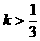 或
或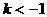
由(3)得: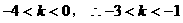
即当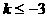 或
或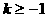 时,三个方程中至少有一个方程有实根。
时,三个方程中至少有一个方程有实根。
8.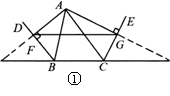 (1)已知:如图①,BD、CE分别是△ABC的外角平
(1)已知:如图①,BD、CE分别是△ABC的外角平
分线,过点A作AF⊥BD,AG⊥CE,垂足分别是
F、G,连结FG,延长AF、AG,与直线BC相交.
 求证:FG=
求证:FG=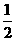 (AB+BC+AC).
(AB+BC+AC).
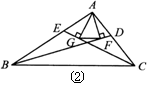
(2)若BD、CE分别是△ABC的内角平分线,其余条件不变
(如图②),线段FG与△ABC的三边又有怎样的数量关系?
写出你的猜想,并给予证明.
7.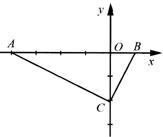
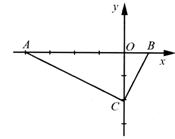 在直角坐标系中,已知A(-4,0)、
在直角坐标系中,已知A(-4,0)、
B(1,0)、C(0,-2)三点.请按以
下要求设计两种方案:作一条与
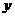 轴不重合,与△ABC的两边相
轴不重合,与△ABC的两边相
交的直线,使截得的三角形与
 △ABC相似,并且面积是△AOC
△ABC相似,并且面积是△AOC
面积的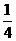 .分别在下面的两个坐标中系画出设计图形,并写出截得的三角形三个顶点的坐标.
.分别在下面的两个坐标中系画出设计图形,并写出截得的三角形三个顶点的坐标.
6.如图( )所示,锐角△ABC中,BC>AB>AC,D、E分别是BC、AB上的动点,连结
)所示,锐角△ABC中,BC>AB>AC,D、E分别是BC、AB上的动点,连结
AD、DE.
(1)当D、E运动时,分别在其余的三个图中画出D、E运动的位置;在图( )中画出仅有一组三角形相似的图形;在图(
)中画出仅有一组三角形相似的图形;在图( )中画出仅有二组三角形相似的图形;在图(
)中画出仅有二组三角形相似的图形;在图(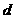 )中画出有三组三角形相似的图形.
)中画出有三组三角形相似的图形.
(2)BC=9,AB=8,AC=6,就图( )求出DE的长.
)求出DE的长.
5.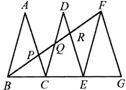 如图,已知,△ABC、△DCE、△FEG是三个全等的等腰
如图,已知,△ABC、△DCE、△FEG是三个全等的等腰
三角形,底边BC、CE、EG在同一直线上,且AB=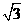 ,
,
BC=1.连结BF,分别交AC、DC、DE于点P、Q、R.
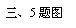 (1)△BFG与△FEG相似吗?为什么?
(1)△BFG与△FEG相似吗?为什么?
(2)写出图中所有与△ABP相似的三角形(不必证明).
4.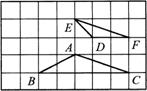 如图,正方形网格中的小正方形的面积都为1,
如图,正方形网格中的小正方形的面积都为1,
网格中有△ABC和△DFE.
(1)这两个三角形相似吗?说出你的理由;
(2)请你以网格中的格点为顶点,在网格中再画出
 一个面积为4且与△ABC相似的三角形.
一个面积为4且与△ABC相似的三角形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com