
题目列表(包括答案和解析)
4.(·湖州市) 已知:在矩形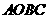 中,
中,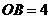 ,
,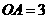 .分别以
.分别以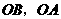 所在直线为
所在直线为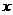 轴和
轴和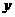 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系.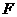 是边
是边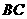 上的一个动点(不与
上的一个动点(不与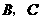 重合),过
重合),过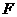 点的反比例函数
点的反比例函数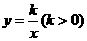 的图象与
的图象与 边交于点
边交于点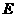 .
.
(1)求证: 与
与 的面积相等;
的面积相等;
(2)记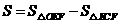 ,求当
,求当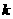 为何值时,
为何值时,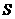 有最大值,最大值为多少?
有最大值,最大值为多少?
(3)请探索:是否存在这样的点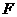 ,使得将
,使得将 沿
沿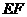 对折后,
对折后,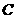 点恰好落在
点恰好落在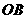 上?若存在,求出点
上?若存在,求出点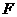 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
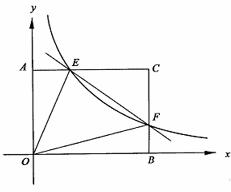









3..(·河南)如图,直线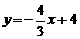 和x轴、y轴的交点分别为B、C,点A的坐标是(-2,0).
和x轴、y轴的交点分别为B、C,点A的坐标是(-2,0).
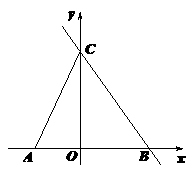

(1)试说明△ABC是等腰三角形;
(2)动点M从A出发沿x轴向点B运动,同时动点N从点B出发沿线段BC向点C运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M运动t秒时,△MON的面积为S.
① 求S与t的函数关系式;
② 设点M在线段OB上运动时,是否存在S=4的情形?若存在,求出对应的t值;若不存在请说明理由;
③在运动过程中,当△MON为直角三角形时,求t的值.









2..(·南京市)如图,已知 的半径为6cm,射线
的半径为6cm,射线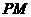 经过点
经过点 ,
,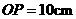 ,射线
,射线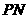 与
与 相切于点
相切于点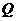 .
.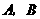 两点同时从点
两点同时从点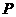 出发,点
出发,点 以5cm/s的速度沿射线
以5cm/s的速度沿射线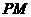 方向运动,点
方向运动,点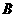 以4cm/s的速度沿射线
以4cm/s的速度沿射线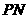 方向运动.设运动时间为
方向运动.设运动时间为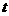 s.
s.
(1)求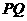 的长;
的长;
(2)当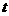 为何值时,直线
为何值时,直线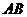 与
与 相切?
相切?










类型之二 存在性动态题
存在性动态题运用几何计算进行探索的综合型问题,要注意相关的条件,可以先假设结论成立,然后通过计算求相应的值,再作存在性的判断. 
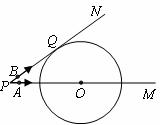
1.(·宜昌市)如图,在Rt△ABC中,AB=AC,P是边AB(含端点)上的动点,过P作BC的垂线PR,R为垂足,∠PRB的平分线与AB相交于点S,在线段RS上存在一点T,若以线段PT为一边作正方形PTEF,其顶点E、F恰好分别在边BC、AC上.
(1)△ABC与△SBR是否相似?说明理由;
(2)请你探索线段TS与PA的长度之间的关系;
(3)设边AB=1,当P在边AB(含端点)上运动时,请你探索正方形PTEF的面积y的最小值和最大值.
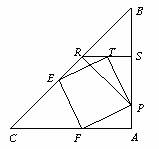









2、如图6,在平面直角坐标系内,Rt△ABC的直角顶点C(0,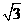 )在
)在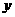 轴的正半轴上,A、B是
轴的正半轴上,A、B是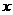 轴上是两点,且OA∶OB=3∶1,以OA、OB为直径的圆分别交AC于点E,交BC于点F.直线EF交OC于点Q.
轴上是两点,且OA∶OB=3∶1,以OA、OB为直径的圆分别交AC于点E,交BC于点F.直线EF交OC于点Q.
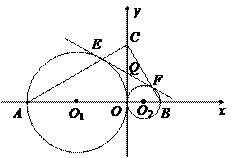
图6
求过A、B、C三点的抛物线的解析式;
请猜想:直线EF与两圆有怎样的位置关系?并证明你的猜想.
在△AOC中,设点M是AC边上的一个动点,过M作MN∥AB交OC于点N.试问:在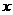 轴上是否存在点P,使得△PMN是一个以MN为一直角边的等腰直角三角形?若存在,求出P点坐标;若不存在,请说明理由.
轴上是否存在点P,使得△PMN是一个以MN为一直角边的等腰直角三角形?若存在,求出P点坐标;若不存在,请说明理由.
1、如图5-1,边长为2的正方形ABCD中,顶点A的坐标是(0,2),一次函数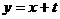 的图象
的图象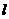 随
随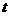 的不同取值变化时,位于
的不同取值变化时,位于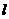 的右下方由
的右下方由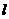 和正方形的边围成的图形面积为
和正方形的边围成的图形面积为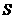 (阴影部分).
(阴影部分).
⑴当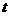 何值时,
何值时,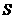 =3?
=3?
⑵在平面直角坐标系下(图5-2),画出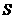 与
与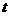 的函数图象.
的函数图象.
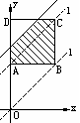

图5-1 图5-2
4、跨学科综合题
跨学科的综合题中,与物理相结合得最多,另外与化学、地理、生物、医药、政治等学科的综合题也时常出现. 多数跨学科试题中,所用的其他学科专业知识很少或者是最基本的. 解题时,主要是运用相关学科中的基本公式或原理分析各种现象.
例5(湖北宜昌)天象图片欣赏:
如图4-1是2004年5月5日2时48分到3时52分在北京拍摄的从初亏到食既的月全食过程.
图4 -1
-1
数学问题解决:
用数学的眼光看图4-1,可以认为是地球、月球投影(两个圆)的位置关系发生了从外切、相交到内切的变化:2时48分月球投影开始进入地球投影的黑影(图4-2);接着月球投影沿直线OP匀速地平行移动进入地球投影的黑影(图4-3);3时52分,这时月球投影全部进入地球投影的黑影(图4-4).
设照片中的地球投影如图2中半径为R的大圆⊙O,月球投影如图2中半径为r的小圆⊙P.求这段时间内圆心距OP与时间t(分)的函数关系式,写出自变量的取值范围.
 分析:从2时48分到3时52分共64分钟,点 P运动的路程为2r,
分析:从2时48分到3时52分共64分钟,点 P运动的路程为2r,
∴点P运动的速度为: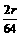 ,即
,即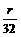 ,
,
∴P点t分钟运动的路程为: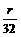 t,
t,
∴OP=R+r-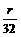 t,(6分),(0≤t≤64)
t,(6分),(0≤t≤64)
3、代数与几何的综合题
代数与几何的综合题主要呈现两种主要类型:
(1)在平面直角坐标系中,由图象构成的几何图形作为研究对象命题. 解此类问题,数形结合思想是关键. 通常要求出特定点的坐标、特定线的解析式,利用函数的方法解决几何问题. 另外,还需熟悉一些常用的解题思路,比如,求坐标系中几何图形的面积,常以一条坐标轴作为底边,或通过坐标轴对图形进行割(补)构造,使之转化为便于求解的面积问题.
(2)以几何为主要载体,借助函数与方程的数学思想方法,研究几何元素间的数量关系. 求几何图形中的函数解析,通常根据相似形或圆幂定理(相交弦定理、切割线定理及其推论)的知识,列出含有变量的等式,然后转化为函数解析式的形式. 自变量的取值范围一般由图形存在的极端情况来确定最大值或最小值. 对于“动点型”的综合题,要学会化动为静,静中求解,动中检验.
例3 (江苏连云港) 如图2,直线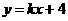 与函数
与函数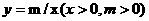 的图象交于A、B两点,且与x、y轴分别交于C、D两点.
的图象交于A、B两点,且与x、y轴分别交于C、D两点.
(1)若 的面积是
的面积是 的面积的
的面积的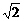 倍,求
倍,求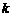 与
与 之间的函数关系式;
之间的函数关系式;
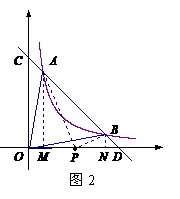 (2)在(1)的条件下,是否存在
(2)在(1)的条件下,是否存在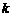 和
和 ,使得以
,使得以 为直径的圆经过点
为直径的圆经过点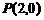 .若存在,求出
.若存在,求出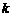 和
和 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
分析:设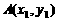 ,
,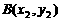 (其中
(其中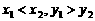 ),
),
由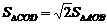 ,得
,得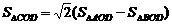
∴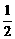 ·
· ·
·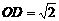 (
(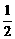 ·
· ·
·
 ·
· ·
·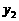 ),
),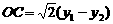 ,
,
又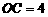 ,∴
,∴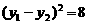 ,即
,即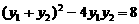 ,
,
由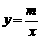 可得
可得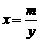 ,代入
,代入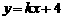 可得
可得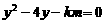 ①
①
∴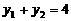 ,
,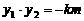 ,
,
∴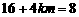 ,即
,即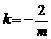 .
.
又方程①的判别式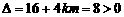 ,
,
∴所求的函数关系式为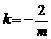
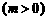 .
.
(2)假设存在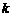 ,
, ,使得以
,使得以 为直径的圆经过点
为直径的圆经过点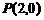 .
.
则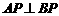 ,过
,过 、
、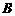 分别作
分别作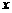 轴的垂线,垂足分别为
轴的垂线,垂足分别为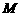 、
、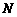 .
.
∵ 与
与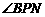 都与
都与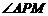 互余,∴
互余,∴
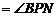 .
.
∴Rt ∽Rt
∽Rt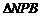 ,∴
,∴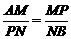 .
.
∴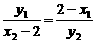 ,∴
,∴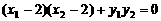 , ∴
, ∴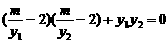 ,
,
即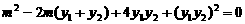 ②
②
由(1)知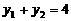 ,
,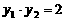 ,代入②得
,代入②得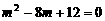 ,
,
∴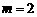 或
或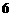 ,又
,又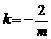 ,∴
,∴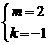 或
或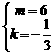 ,
,
∴存在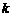 ,
, ,使得以
,使得以 为直径的圆经过点
为直径的圆经过点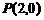 ,且
,且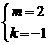 或
或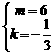 .
.
例4(北京石景山)已知:如图3,等边△ABC中,AB、cosB是关于x的方程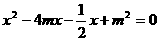 的两个实数根. 若D、E分别是BC、AC上的点,且∠ADE=60°,设BD=x,AE=y,求y关于x的函数关系式,并求出y的最小值.
的两个实数根. 若D、E分别是BC、AC上的点,且∠ADE=60°,设BD=x,AE=y,求y关于x的函数关系式,并求出y的最小值.
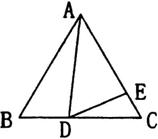
图3
分析:(1)∵△ABC是等边三角形
∴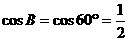
∴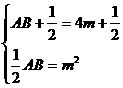
解得: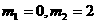
∵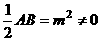
∵m=0不合题意,舍去
∴m=2即AB=8
(2)∵∠ADE=60°
∴∠ADB+∠CDE=120°
又∠ADB+∠BAD=180°-∠B=120°
∴∠BAD=∠CDE
又∵∠B=∠C=60°
∴△ABD∽△DCE
∴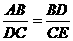
设BD=x,EA=y则DC=8-x,CE=8-y
∴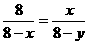
∴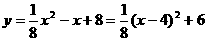
∴当BD=4,即D为BC的中点时,EA有最小值6.
2、几何综合题
几何知识大致可以分成直线形(包括线与角、三角形、四边形)、相似形、三角函数、圆四个知识块,各知识块之间的联系较为密切,都能形成综合题. 其中,与圆或三角函数的几何综合题为主. 对于几何各知识之间相结合形成的综合题,既要能从复杂的图形背景中分离出基本图形,又要善于发现各基本图形以及相关定理之间的联系.
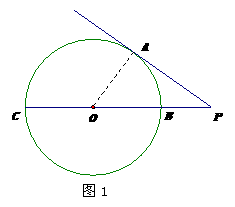
例2(浙江宁波)如图1,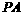 切⊙
切⊙ 于
于 ,割线
,割线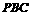 经过圆心
经过圆心 ,交⊙
,交⊙ 于B、C两点,若
于B、C两点,若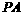
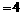 ,
,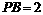 ,则
,则 的值为( )
的值为( )
 A.
A.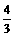 B.
B.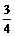 C.
C.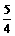 D.
D.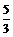
分析:由切割线定理,得PA2 = PB·PC,则42 = 2 PC,解得PC = 8,所以
BC=PC-PB=8-2=6,OA = OB = BC/2 =3,PO = PB+OB = 2+3 =5.
连结AO,由于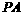 切⊙
切⊙ 于
于 ,所以∠OAP = 900.
,所以∠OAP = 900.
在Rt△POA中,OA = = 3,  = OA/AP = 3/4.
= OA/AP = 3/4.
故选B.
1、代数综合题
代数各知识点之间,以函数与方程的综合题为主,有时还可以与不等式的知识相结合,用来确定自变量的取值范围. 函数与方程的综合题中,二者的联系表现在:
(1)求函数值,或由函数值求自变量的问题,转化为相应的方程问题;
(2)求函数的解析式,往往要根据题意列出方程或者方程组求解;
(3)以x为自变量的函数y,其图象与x轴(y轴)的交点问题,即为求当y=0(x=0)时的方程的解的问题;
(4)两个函数图像的交点问题,就是由两个函数解析式组成的方程组的解的问题.
例1(福建南平)已知一次函数y = - x + 4 与反比例函数y = k / x在同一直角坐标系内的图象没有交点,则k的取值范围是( )
A.k>0; B.k<4; C.k> - 4; D.k>4.
分析:由两个函数解析式组成方程组,可得k / x = - x + 4.
去分母,得 x2 – 4x + k = 0.
两个函数的图象没有交点,说明以上方程没有实数根,则
△ = (- 4 )2 - 4 k = 16 – 4k < 0.
解得k>4. 故选D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com