
题目列表(包括答案和解析)
列代数时要按要求规范地书写。像数字与字母、字母与字母相乘可省略乘号不写,数与数相乘必须写乘号;除法可写成分数形式,带 分数与字母相乘需把代分数化为假分数,书写单位名称什么时不加括号,什么时要加括号。注意代数式括号的适当运用。
列代数式时,一般应在语言叙述的数量关系中,先读的先写,如a的2倍与b的3倍的差,为2a-3b,不同级运算的语言,且又要体现出先低级运算,要把代数式中代表低级运算的这部分括起来,如a与b的差的3倍,为3(a-b)。
要正确列代数式,只有分清数量之间的关系。如比m大3的数应为m+3;比一个数大3的数是m,则这个数为m-3;一个数是a的3位,这个数为3a;a是这个数的3倍,这个数为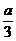 。不要见多就加,见小就减,见倍就乘。
。不要见多就加,见小就减,见倍就乘。
列代数式时,要先认真审题,抓住关键词语,仔细辩析词义。如“除”与“除以”,“平方的差(或平方差)”与“差的平方”的词义区分。例:“3除a”,“被3除得a”,“a与b两数的平方差”,“a与b两数差的平方”,分别为“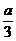 ”、“ 3a”、a2-b2、(a-b)2。
”、“ 3a”、a2-b2、(a-b)2。
4. 反向延长射线构造平角
例4 如图4,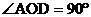 ,OD为
,OD为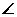 BOC的平分线,OE为BO的延长线。
BOC的平分线,OE为BO的延长线。
求证: COE=2
COE=2 AOB。
AOB。
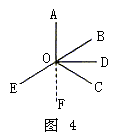
证明:反向延长射线AO得射线OF
因为 AOD为直角,
AOD为直角,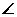 AOF为平角
AOF为平角
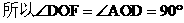
3. 过直线上一点作射线构造平角
例3 如图3,已知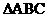 ,求证:
,求证: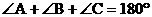
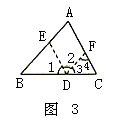
证明:在BC上取一点D(点D不与B、C重合),过点D分别作DE//AC交AB于E,DF//AB交AC于F
因为DE//AC
所以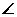 1=
1=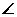 C,
C,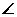 2=
2=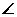 4
4
因为DF//AB 所以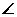 4=
4=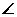 A
A
所以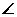 2=
2=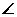 A
A
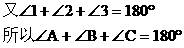
2. 过某点作直线构造平角
例2 如图2,已知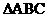 ,求证:
,求证: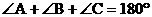 。
。
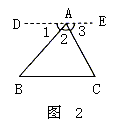
证明:过点A作DE//BC,则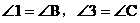
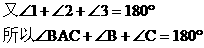
1. 延长线段构造平角
例1 如图1,AB//CD。求证: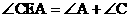
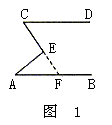
证明:延长CE交AB于点F
因为AB//CD 所以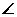 C=
C=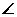 CFA
CFA

1、 在如图的方格纸中(每个小方格的边长都是1个单位)有一点O和△ABC。
(1)请以点O为位似中心,把△ABC缩小为原来的一半(不改变方向),得到△A′B′C′;
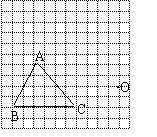 (2)请用适当的方式描述△A′B′C′的顶点A′、B′、C′的位置。
(2)请用适当的方式描述△A′B′C′的顶点A′、B′、C′的位置。
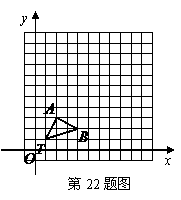
3、在边长为1的方格纸中建立直角坐标系 ,O、A、B三点均为格点.
,O、A、B三点均为格点.
(1)直接写出线段OB的长;
(2)将△OAB绕点O沿逆时针方向旋转90°
得到△OA′B′.请你画出△OA′B′,并求
在旋转过程中,点B所经过的路径 的长度.
的长度.
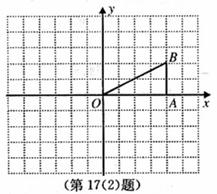
如图,在 中,
中,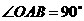 ,且点
,且点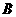 的坐标为(4,2).
的坐标为(4,2).
①画出 向下平移3个单位后的
向下平移3个单位后的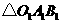 ;
;
②画出 绕点
绕点 逆时针旋转
逆时针旋转 后的
后的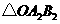 ,并求点
,并求点 旋转到点
旋转到点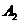 所经过的路线长(结果保留
所经过的路线长(结果保留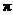 ).
).
(2)①图略;②图略;
点 旋转到点
旋转到点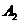 所经过的路线长
所经过的路线长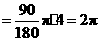 .
.
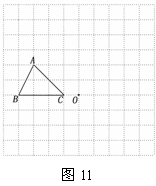 在如图11的方格纸中,每个小方格都是边长为1个单位的正方形,
在如图11的方格纸中,每个小方格都是边长为1个单位的正方形, 的三个顶点都在格点上(每个小方格的顶点叫格点).
的三个顶点都在格点上(每个小方格的顶点叫格点).
(1) 画出 绕点
绕点 顺时针旋转
顺时针旋转 后的
后的 ;
;
(2)求点 旋转到
旋转到 所经过的路线长.
所经过的路线长.
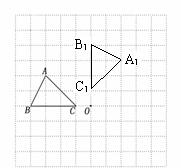 (1)如图:
(1)如图:
······························ 3分
(2) ∵ 点 旋转到
旋转到 所经过的路线长为以OA为半径圆的周长的
所经过的路线长为以OA为半径圆的周长的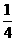 , ··········· 5分
, ··········· 5分
∴ 点 旋转到
旋转到 所经过的路线长为
所经过的路线长为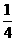 ×2
×2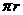 =
=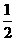
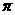 ×
×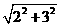 =
=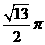 . ·········· 8分
. ·········· 8分
 如图,方格纸中有一条美丽可爱的小金鱼.
如图,方格纸中有一条美丽可爱的小金鱼.
(1)在同一方格纸中,画出将小金鱼图案绕原点O
旋转180°后得到的图案;(4分)
(2)在同一方格纸中,并在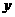 轴的右侧,将原小
轴的右侧,将原小
金鱼图案以原点O为位似中心放大,使它们的位似
比为1:2,画出放大后小金鱼的图案.(4分)

在平面直角坐标系中,已知 ,
,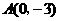 ,
,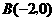 .
.
(1)将 关于点
关于点 对称,在图1中画出对称后的图形,并涂黑;
对称,在图1中画出对称后的图形,并涂黑;
 (2)将
(2)将 先向右平移3个单位,再向上平移2个单位,在图2中画出平移后的图形,并涂黑.
先向右平移3个单位,再向上平移2个单位,在图2中画出平移后的图形,并涂黑.
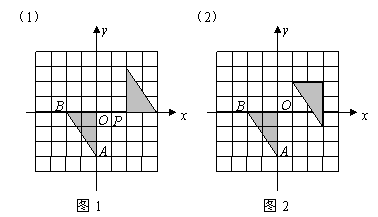
如图,在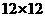 的正方形网格中,
的正方形网格中, 的顶点分别为
的顶点分别为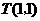 ,
,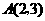 ,
,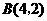 .
.
(1)以点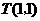 为位似中心,按比例尺
为位似中心,按比例尺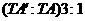 的位似中心的同侧将
的位似中心的同侧将 放大为
放大为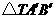 ,放大后点
,放大后点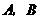 的对应点分别为
的对应点分别为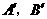 ,画出
,画出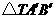 ,并写出点
,并写出点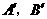 的坐标;
的坐标;
(2)在(1)中,若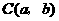 为线段
为线段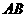 上任一点,写出变化后点
上任一点,写出变化后点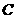 的对应点
的对应点 的坐标.
的坐标.
 (1)画图略
(1)画图略
点A′的坐标为(4,7 ), 点B′的坐标为(10,4 );
(2)点C′的坐标为(3a-2,3b-2 ) .
如图,正方形网格中, 为格点三角形(顶点都是格点),将
为格点三角形(顶点都是格点),将 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 得到
得到 .
.
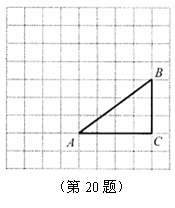 (1)在正方形网格中,作出
(1)在正方形网格中,作出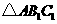 ;
;
(2)设网格小正方形的边长为1,求旋转
过程中动点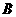 所经过的路径长.
所经过的路径长.
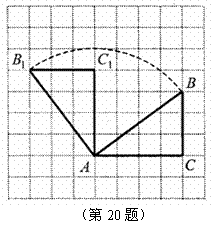
(1)如图
(2)旋转过程中动点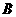 所经过的路径为一段圆弧.
所经过的路径为一段圆弧.
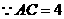 ,
,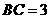 ,
,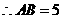 .
.
又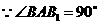 ,
,
 动点
动点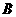 所经过的路径长为
所经过的路径长为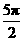 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com