
题目列表(包括答案和解析)
4、相似形计算题
相似形是解直角三角形和圆等知识的基础,特别是在圆中,相似形、比例线段更是所处可见。这部分知识出现在计算题中的也有很多:比例及其性质、相似形的性质、平行线分线段成比例定理等等,另外,引入参数法等重要的数学方法在解题时也经常用到。
例4(山东泰安)有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE(如图4),则CD等于( )
A.25/4; B.22/3; C.7/4; D.5/3.
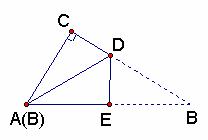
图4
分析:Rt△ABC中,由勾股定理,得AB = =10cm.
将△ABC折叠,使点B与点A重合,点B与点A关于折痕所在直线DE对称,则DE垂直平分AB,BE=AB/2=5 cm.
易证Rt△BDE∽Rt△BAC,则BD:BE=AB:BC,所以
BD = = = .
因此,CD = BC-BD = 8-25/4 =7/4.
故选C.
3、四边形计算题
随着对圆的计算、证明要求的降低,很多省市的几何中考重点开始向以四边形为主的内容转移。比如,河北省连续多年把压轴题锁定在以四边形、三角形为主的直线型图形上。四边形计算题主要的运用知识有:多边形内角和定理及其推论(外角和定理),各种平行四边形及梯形的性质,平行线等分线段定理,三角形及梯形的中位线定理,四边形的周长尤其是面积的求法,对称问题,折痕问题等。
例3(北京海淀)已知:如图3所示,梯形ABCD中,AD//BC,BD平分∠ABC,∠A=120°,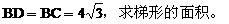
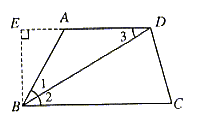
图3
分析:此题解法较多,下面提供其一,希望同学们在多想几种解法,分析所用知识点,比较优劣,以便在中考试有所选择,提高解题效率。
过点B作BE⊥DA交DA的延长线于E。
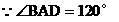
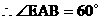
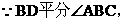
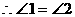
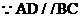

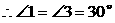
在Rt△BDE中, 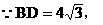
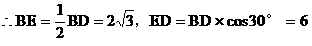
在Rt△BEA中, 

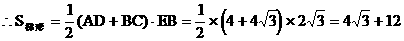
2、三角形计算题
三角形的内角和定理、三边关系定理及其推论,等腰三角形的性质、全等三角形的性质、特殊三角形(比如等边三角形、含有300的直角三角形)的性质、勾股定理、边长、周长及面积的计算等都是三角形计算题的常用知识。解三角形计算题时也经常用到线与角的知识。
例2(江苏连云港)如图2,平面镜A与B之间夹角为110°,光线经平面镜A反射到平面镜B上,再反射出去,若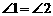 ,则
,则 的度数为___________.
的度数为___________.
 分析:根据光的反射定律可知,∠1=∠3,∠2=∠4.
分析:根据光的反射定律可知,∠1=∠3,∠2=∠4.
因为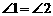 ,所以∠3 =∠4.
,所以∠3 =∠4.
则∠3 、∠4成为顶角为1100角的等腰三角形的两个底角,
因此,∠1 = (1800 – 1100) = ×700 = 350.
1、线与角计算题
所用知识主要有线段的中点、角平分线、线段或角的和差倍分、余角、补角的基本概念的定义,以及角的计量、对顶角性质、平行线性质等。难度不大,可直接利用上述定义、定理解题。
例1(黑龙江)如图1,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=____________.
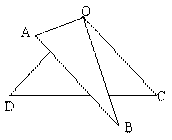
图1
分析:∠AOC+∠DOB
= (∠AOD+∠DOB+∠COB)+∠DOB
= (∠AOD+∠DOB)+(∠COB+∠DOB)
= ∠AOB + ∠COD
= 900 + 900
= 1800.
几何计算题的重点比较分散,从知识点本身来说,解直角三角形的知识具有计算题得天独厚的优势,所以涉及解直角三角形的试题大部分是计算题。但是,在实际命题时,更多的是圆的有关计算题和四边形的计算题,它们与其它几何知识都有密切的联系,能在主要考查一个知识点的同时,考查其他知识点。就题型而言,各种题型中都能见到几何计算题的身影,比如线与角计算题、三角形计算题、相似形计算题等等,综合性计算题则更多出现在中档解答题和压轴题中。
需要说明的是,根据中考命题改革的大趋势,几何计算题的难度比以前有所下降,更突出在题目的内容、形式、解法上有所创新,所以,我们不必把重点放到一些繁难的计算题上,而应扎实学好基础知识,多分析解题使用到的数学思想方法,比如方程与函数、分类讨论、转化构造等数学思想方法,重视数学知识的实际应用。
如图1所示:

证明与计算,是几何命题的两大核心内容。几何计算题,通常需要借助几何中的概念、定义、定理、公理等知识,求解相关几何元素的数值。在解题时,要求能准确灵活地选用有关知识,采用各种数学方法(既可以是几何方法,也可以是代数方法),加以求解。为了能在有限的时间内,迅速准确地解题,就需要在平时练习中,强化基础题,多采用一题多解、优化方案等训练方法,积累经验,达到熟能生巧的效果。
6.如图17,已知抛物线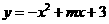 与x轴的一个交点
与x轴的一个交点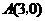 .
.
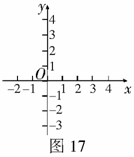
(1)你一定能分别求出这条抛物线与x轴的另一个交点B及与y轴的交点C的坐标,试试看;
(2)设抛物线的顶点为D,请在图中画出抛物线的草图.若点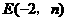 在直线BC上,试判断E点是否在经过D点的反比例函数的图象上,把你的判断过程写出来;
在直线BC上,试判断E点是否在经过D点的反比例函数的图象上,把你的判断过程写出来;
(3)请设法求出tan∠DAC的值.
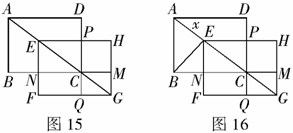
5.如图15,矩形ABCD中,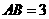 ,
, ,将矩形ABCD沿对角线AC平移,平移后的矩形为EFGH(A、E、C、G始终在同一条直线上),当点E与C重合时停止移动.平移中EF与BC交于点N,GH与BC的延长线交于点M,EH与DC交于点P,FG与DC的延长线交于点Q.设S表示矩形PCMH的面积,
,将矩形ABCD沿对角线AC平移,平移后的矩形为EFGH(A、E、C、G始终在同一条直线上),当点E与C重合时停止移动.平移中EF与BC交于点N,GH与BC的延长线交于点M,EH与DC交于点P,FG与DC的延长线交于点Q.设S表示矩形PCMH的面积,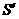 表示矩形NFQC的面积.
表示矩形NFQC的面积.
(1) 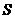 与
与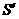 相等吗?请说明理由.
相等吗?请说明理由.
(2)设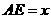 ,写出S和x之间的函数关系式,并求出x取何值时S有最大值,最大值是多少?
,写出S和x之间的函数关系式,并求出x取何值时S有最大值,最大值是多少?
(3)如图16,连结BE,当AE为何值时, 是等腰三角形.
是等腰三角形.
4.在社会主义新农村建设中,李叔叔承包了家乡的50亩荒山.经过市场调查,预测水果上市后A种水果每年每亩可获利0.3万元,B种水果每年每亩可获利0.2万元,李叔叔决定在承包的山上种植A、B两种水果.他了解到需要一次性投入的成本为:A种水果每亩1万元,B种水果每亩0.9万元.设种植A种水果x亩,投入成本总共y万元.
(1)求y与x之间的函数关系式;
(2)若李叔叔在开发时投入的资金不超过47万元,为使总利润每年不少于11.8万元,应如何安排种植面积(亩数x取整数)?请写出获利最大的种植方案.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com