
题目列表(包括答案和解析)
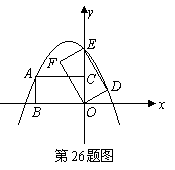
26.如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).
(1)求A、B两点的坐标;
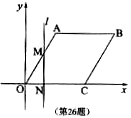 (2)设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;
(2)设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;
(3)在题(2)的条件下,t为何值时,S的面积最大?最大面积是多少?
2008年呼和浩特
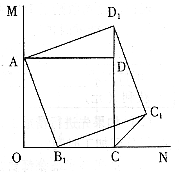
25、如图:∠MON = 90°,在∠MON的内部有一个正方形AOCD,点A、C分别在射线OM、ON上,点B1是ON上的任意一点,在∠MON的内部作正方形AB1C1D1。
(1)连续D1D,求证:∠ADD1 = 90°;
(2)连结CC1,猜一猜,∠C1CN的度数是多少?并证明你的结论;
(3)在ON上再任取一点B2,以AB2为边,在∠MON的内部作正方形AB2C2D2,观察图形,并结合(1)、(2)的结论,请你再做出一个合理的判断。
2006年锦州市
1.
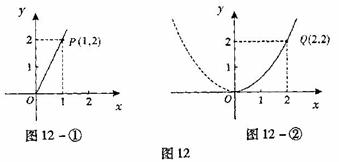
随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高. 某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润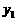 与投资量x成正比例关系,如图12-①所示;种植花卉的利润
与投资量x成正比例关系,如图12-①所示;种植花卉的利润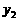 与投资量x成二次函数关系,如图12-②所示(注:利润与投资量的单位:万元).
与投资量x成二次函数关系,如图12-②所示(注:利润与投资量的单位:万元).
(1)分别求出利润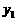 与
与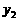 关于投资量x的函数关系式;
关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获得的最大利润是多少?
北京08
已知等边三角形纸片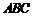 的边长为
的边长为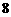 ,
,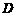 为
为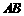 边上的点,过点
边上的点,过点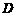 作
作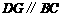 交
交 于点
于点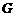 .
.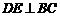 于点
于点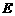 ,过点
,过点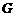 作
作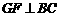 于点
于点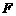 ,把三角形纸片
,把三角形纸片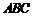 分别沿
分别沿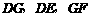 按图1所示方式折叠,点
按图1所示方式折叠,点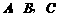 分别落在点
分别落在点 ,
,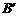 ,
,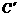 处.若点
处.若点 ,
,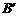 ,
,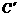 在矩形
在矩形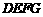 内或其边上,且互不重合,此时我们称
内或其边上,且互不重合,此时我们称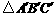 (即图中阴影部分)为“重叠三角形”.
(即图中阴影部分)为“重叠三角形”.

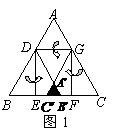
(1)若把三角形纸片 放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点
放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点 恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形
恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形 的面积;
的面积;
(2)实验探究:设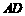 的长为
的长为 ,若重叠三角形
,若重叠三角形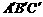 存在.试用含
存在.试用含 的代数式表示重叠三角形
的代数式表示重叠三角形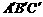 的面积,并写出
的面积,并写出 的取值范围(直接写出结果,备用图供实验,探究使用).
的取值范围(直接写出结果,备用图供实验,探究使用).
解:(1)重叠三角形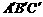 的面积为
;
的面积为
;
(2)用含 的代数式表示重叠三角形
的代数式表示重叠三角形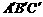 的面积为
;
的面积为
; 的取值范围为 .
的取值范围为 .
德州市2006
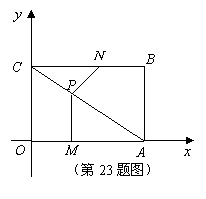
如图,平面直角坐标系中,四边形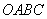 为矩形,点
为矩形,点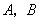 的坐标分别为
的坐标分别为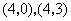 ,动点
,动点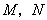 分别从
分别从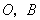 同时出发,以每秒1个单位的速度运动.其中,点M沿
同时出发,以每秒1个单位的速度运动.其中,点M沿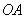 向终点
向终点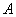 运动,点
运动,点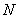 沿
沿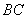 向终点
向终点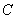 运动,过点M作
运动,过点M作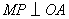 ,交
,交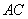 于
于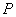 ,连结
,连结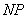 .已知动点运动了
.已知动点运动了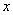 秒.
秒.
(1)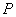 点的坐标为(
,
)(用含
点的坐标为(
,
)(用含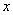 的代数式表示);
的代数式表示);
(2)试求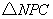 面积
面积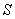 的表达式,并求出面积
的表达式,并求出面积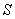 的最大值及相应的
的最大值及相应的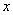 值;
值;
(3)当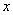 为何值时,
为何值时, 是一个等腰三角形?简要说明理由.
是一个等腰三角形?简要说明理由.
眉山市2006
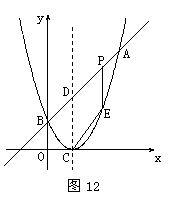
24.(本大题满分14分)如图12,已知二次函数图象的顶点坐标为C(1,0),直线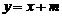 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴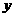 上.
上.
(1)求 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作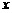 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为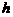 ,点P的横坐标为
,点P的横坐标为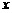 ,求
,求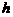 与
与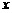 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量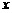 的取值范围;
的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
南宁市08
25.(08山东聊城25题)(本题满分12分)如图,把一张长10cm,宽8cm的矩形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).

(1)要使长方体盒子的底面积为48cm2,那么剪去的正方形的边长为多少?
(2)你感到折合而成的长方体盒子的侧面积会不会有更大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由;
(3)如果把矩形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的矩形,然后折合成一个有盖的长方体盒子,是否有侧面积最大的情况;如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由.
2008年云南省
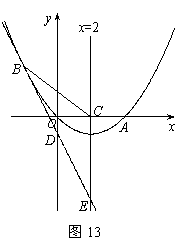
24. (本题满分14分)如图13,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2 与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.
(1)求m的值及该抛物线对应的函数关系式;
(2)求证:① CB=CE ;② D是BE的中点;
(3)若P(x,y)是该抛物线上的一个动点,是否存在这样的点P,使得PB=PE,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
(08辽宁沈阳26题)(本题14分)26.如图所示,在平面直角坐标系中,矩形 的边
的边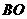 在
在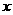 轴的负半轴上,边
轴的负半轴上,边 在
在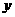 轴的正半轴上,且
轴的正半轴上,且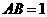 ,
,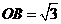 ,矩形
,矩形 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转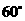 后得到矩形
后得到矩形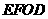 .点
.点 的对应点为点
的对应点为点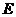 ,点
,点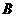 的对应点为点
的对应点为点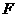 ,点
,点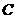 的对应点为点
的对应点为点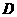 ,抛物线
,抛物线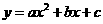 过点
过点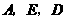 .
.
(1)判断点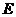 是否在
是否在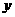 轴上,并说明理由;
轴上,并说明理由;
(2)求抛物线的函数表达式;
 (3)在
(3)在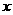 轴的上方是否存在点
轴的上方是否存在点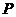 ,点
,点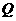 ,使以点
,使以点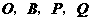 为顶点的平行四边形的面积是矩形
为顶点的平行四边形的面积是矩形 面积的2倍,且点
面积的2倍,且点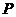 在抛物线上,若存在,请求出点
在抛物线上,若存在,请求出点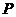 ,点
,点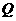 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
24.(本小题满分12分)
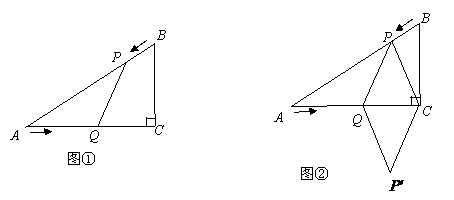
已知:如图①,在 中,
中,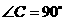 ,
,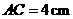 ,
,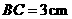 ,点
,点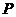 由
由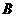 出发沿
出发沿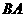 方向向点
方向向点 匀速运动,速度为1cm/s;点
匀速运动,速度为1cm/s;点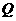 由
由 出发沿
出发沿 方向向点
方向向点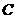 匀速运动,速度为2cm/s;连接
匀速运动,速度为2cm/s;连接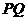 .若设运动的时间为
.若设运动的时间为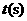 (
(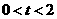 ),解答下列问题:
),解答下列问题:
(1)当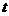 为何值时,
为何值时,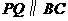 ?
?
(2)设 的面积为
的面积为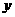 (
(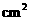 ),求
),求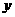 与
与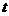 之间的函数关系式;
之间的函数关系式;
(3)是否存在某一时刻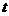 ,使线段
,使线段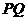 恰好把
恰好把 的周长和面积同时平分?若存在,求出此时
的周长和面积同时平分?若存在,求出此时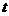 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(4)如图②,连接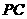 ,并把
,并把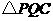 沿
沿 翻折,得到四边形
翻折,得到四边形 ,那么是否存在某一时刻
,那么是否存在某一时刻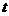 ,使四边形
,使四边形 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
海南省2008
25.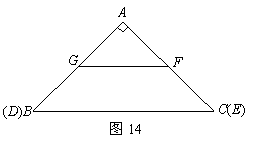 如图14,在
如图14,在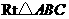 中,
中,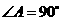 ,
,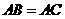 ,
,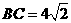 ,另有一等腰梯形
,另有一等腰梯形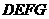 (
(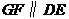 )的底边
)的底边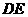 与
与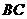 重合,两腰分别落在
重合,两腰分别落在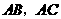 上,且
上,且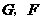 分别是
分别是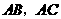 的中点.
的中点.
(1)求等腰梯形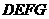 的面积;
的面积;
(2)操作:固定 ,将等腰梯形
,将等腰梯形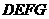 以每秒1个单位的速度沿
以每秒1个单位的速度沿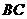 方向向右运动,直到点
方向向右运动,直到点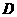 与点
与点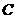 重合时停止.设运动时间为
重合时停止.设运动时间为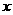 秒,运动后的等腰梯形为
秒,运动后的等腰梯形为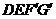 (如图15).
(如图15).
探究1:在运动过程中,四边形 能否是菱形?若能,请求出此时
能否是菱形?若能,请求出此时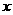 的值;若不能,请说明理由.
的值;若不能,请说明理由.
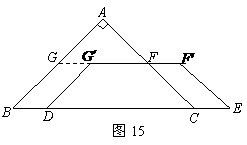
探究2:设在运动过程中 与等腰梯形
与等腰梯形 重叠部分的面积为
重叠部分的面积为 ,求
,求 与
与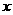 的函数关系式.
的函数关系式.
二○○八山东省青岛市
19.(本题满分8分)四川汶川大地震发生后,我市某工厂 车间接到生产一批帐篷的紧急任务,要求必须在12天(含12天)内完成.已知每顶帐篷的成本价为800元,该车间平时每天能生产帐篷20顶.为了加快进度,车间采取工人分批日夜加班,机器满负荷运转的生产方式,生产效率得到了提高.这样,第一天生产了22顶,以后每天生产的帐篷都比前一天多2顶.由于机器损耗等原因,当每天生产的帐篷数达到30顶后,每增加1顶帐篷,当天生产的所有帐篷,平均每顶的成本就增加20元.设生产这批帐篷的时间为
车间接到生产一批帐篷的紧急任务,要求必须在12天(含12天)内完成.已知每顶帐篷的成本价为800元,该车间平时每天能生产帐篷20顶.为了加快进度,车间采取工人分批日夜加班,机器满负荷运转的生产方式,生产效率得到了提高.这样,第一天生产了22顶,以后每天生产的帐篷都比前一天多2顶.由于机器损耗等原因,当每天生产的帐篷数达到30顶后,每增加1顶帐篷,当天生产的所有帐篷,平均每顶的成本就增加20元.设生产这批帐篷的时间为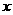 天,每天生产的帐篷为
天,每天生产的帐篷为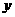 顶.
顶.
(1)直接写出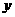 与
与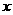 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量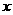 的取值范围.
的取值范围.
(2)若这批帐篷的订购价格为每顶1200元,该车间决定把获得最高利润的那一天的全部利润捐献给灾区.设该车间每天的利润为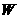 元,试求出
元,试求出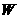 与
与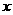 之间的函数关系式,并求出该车间捐款给灾区多少钱?
之间的函数关系式,并求出该车间捐款给灾区多少钱?
2008年辽宁省十二市
25.将两块含30°角且大小相同的直角三角板如图1摆放。
(1)将图1中△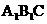 绕点C顺时针旋转45°得图2,点
绕点C顺时针旋转45°得图2,点 与AB的交点,求证:
与AB的交点,求证: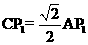 ;
;
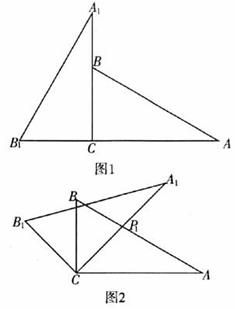
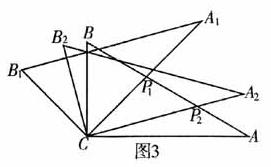 (2)将图2中△
(2)将图2中△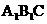 绕点C顺时针旋转30°到△
绕点C顺时针旋转30°到△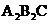 (如图3),点
(如图3),点 与AB的交点。线段
与AB的交点。线段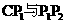 之间存在一个确定的等量关系,请你写出这个关系式并说明理由;
之间存在一个确定的等量关系,请你写出这个关系式并说明理由;
(3)将图3中线段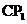 绕点C顺时针旋转60°到
绕点C顺时针旋转60°到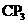 (如图4),连结
(如图4),连结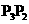 ,
,
求证: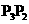 ⊥AB.
⊥AB. 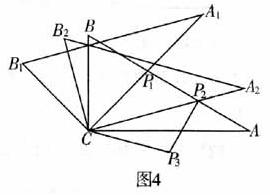
黄冈市2008
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com