
题目列表(包括答案和解析)
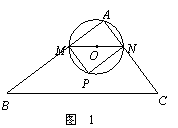
20、如图,在 中
中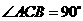 ,
,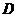 是
是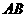 的中点,以
的中点,以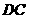 为直径的
为直径的 交
交 的三边,交点分别是
的三边,交点分别是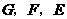 点.
点.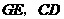 的交点为
的交点为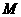 ,且
,且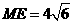 ,
, .
.
(1)求证: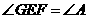 .
.
(2)求 的直径
的直径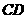 的长.
的长.
(3)若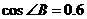 ,以
,以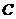 为坐标原点,
为坐标原点,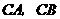 所在的直线分别为
所在的直线分别为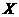 轴和
轴和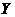 轴,建立平面直角坐标系,求直线
轴,建立平面直角坐标系,求直线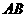 的函数表达式.
的函数表达式.

答案:(1)连接DF
∵CD是圆直径 ∴∠CFD=90°即DF⊥BC
∵∠ACB=90°∴DF ∥AC
∴∠BDF=∠A
∵在⊙O中∠BDF=∠GEF ∴∠GEF=∠A
(2) ∵D是Rt△ABC斜边AB的中点,
∴DC=DA
∴∠DCA=∠A
又由(1)知∠GEF=∠A ∴∠DCA=∠GEF
又∵∠OME=∠EMC ∴△OME与△EMC相似
∴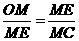 ∴
∴ 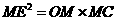
又∵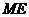 =
=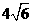 ∴
∴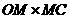 =
=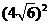 =96
=96
∵MD:CO=2:5 ∴OM:MD=3:2 ∴ OM:MC=3:8
设OM=3 MC=8
MC=8 ∴
∴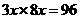 ∴
∴ =2
=2
直径CD=10x=20
(3) ∵Rt△ABC斜边AB的中线CD=20 ∴AB=40
∵在Rt△ABC中,cos∠B=0.6=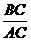 ∴BC=24 ∴ AC=32
∴BC=24 ∴ AC=32
设直线AB的函数表达式为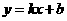 根据题意得 A (32,0) B(0,24)
根据题意得 A (32,0) B(0,24)
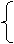
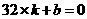
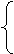
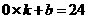 解得
解得 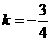
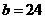 ∴
∴
∴直线AB的函数解析式为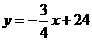
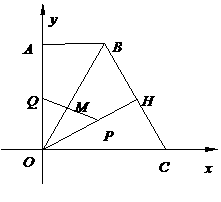
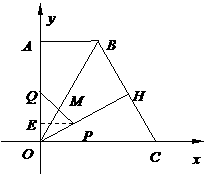
19.(本题满分12分)
如图,直角梯形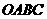 中,
中,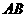 ∥
∥ ,
, 为坐标原点,点
为坐标原点,点 在
在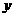 轴正半轴上,点
轴正半轴上,点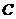 在
在 轴正半轴上,点
轴正半轴上,点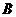 坐标为(2,2
坐标为(2,2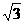 ),∠
),∠ = 60°,
= 60°,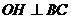 于点
于点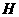 .动点
.动点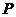 从点
从点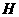 出发,沿线段
出发,沿线段 向点
向点 运动,动点
运动,动点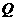 从点
从点 出发,沿线段
出发,沿线段 向点
向点 运动,两点同时出发,速度都为每秒1个单位长度.设点
运动,两点同时出发,速度都为每秒1个单位长度.设点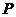 运动的时间为
运动的时间为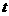 秒.
秒.
(1)
求 的长;
的长;
(2)
若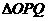 的面积为
的面积为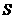 (平方单位). 求
(平方单位). 求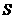 与
与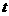 之间的函数关系式.并求
之间的函数关系式.并求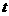 为何值时,
为何值时,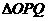 的面积最大,最大值是多少?
的面积最大,最大值是多少?
(3)
设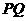 与
与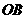 交于点
交于点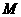 .①当△
.①当△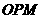 为等腰三角形时,求(2)中
为等腰三角形时,求(2)中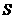 的值.
的值.
②探究线段 长度的最大值是多少,直接写出结论.
长度的最大值是多少,直接写出结论.
答案:
解:(1)∵ ∥
∥
∴ 
在 中,
中,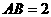 ,
,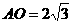
∴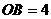 ,
, 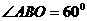
∴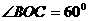 而
而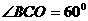
∴ 为等边三角形
为等边三角形
∴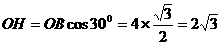 …(3分)
…(3分)
(2)∵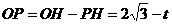
∴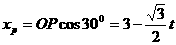
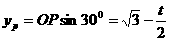
∴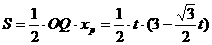
=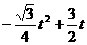 (
(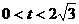 )…………………………(6分)
)…………………………(6分)
即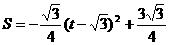
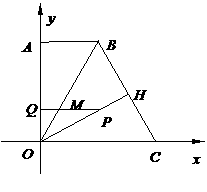 ∴当
∴当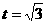 时,
时,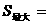
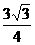 ………………………………………(7分)
………………………………………(7分)
(3)①若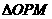 为等腰三角形,则:
为等腰三角形,则:
(i)若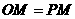 ,
,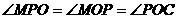
∴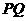 ∥
∥
∴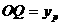 即
即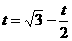
解得: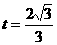
 此时
此时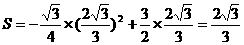 ………………………………(8分)
………………………………(8分)
(ii)若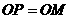 ,
,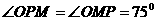
∴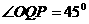
过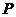 点作
点作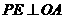 ,垂足为
,垂足为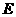 ,则有:
,则有:
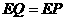
即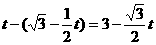
解得: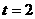
此时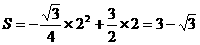 ……………………………………(9分)
……………………………………(9分)
(iii)若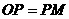 ,
,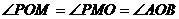
∴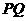 ∥
∥
此时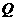 在
在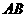 上,不满足题意.……………………………………………(10分)
上,不满足题意.……………………………………………(10分)
②线段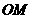 长的最大值为
长的最大值为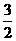 ……………………………………………………(12分)
……………………………………………………(12分)
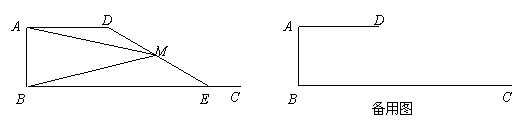
18、(2008上海)已知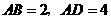 ,
,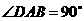 ,
,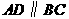 (如图).
(如图).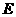 是射线
是射线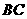 上的动点(点
上的动点(点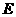 与点
与点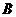 不重合),
不重合),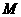 是线段
是线段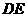 的中点.
的中点.
(1)设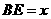 ,
,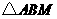 的面积为
的面积为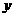 ,求
,求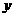 关于
关于 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(2)如果以线段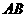 为直径的圆与以线段
为直径的圆与以线段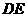 为直径的圆外切,求线段
为直径的圆外切,求线段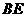 的长;
的长;
(3)联结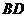 ,交线段
,交线段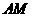 于点
于点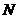 ,如果以
,如果以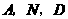 为顶点的三角形与
为顶点的三角形与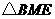 相似,求线段
相似,求线段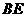 的长.
的长.

答案:解:(1)取 中点
中点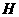 ,联结
,联结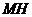 ,
,
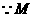 为
为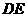 的中点,
的中点,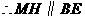 ,
,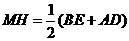 .
.
又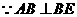 ,
,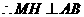 .
.
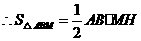 ,得
,得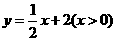 ;
;
(2)由已知得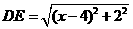 .
.
 以线段
以线段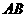 为直径的圆与以线段
为直径的圆与以线段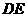 为直径的圆外切,
为直径的圆外切,
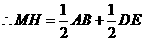 ,即
,即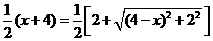 .
.
解得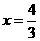 ,即线段
,即线段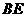 的长为
的长为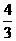 ;
;
(3)由已知,以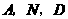 为顶点的三角形与
为顶点的三角形与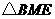 相似,
相似,
又易证得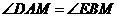 .
.
由此可知,另一对对应角相等有两种情况:①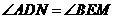 ;②
;②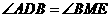 .
.
①当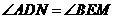 时,
时,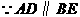 ,
,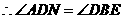 .
.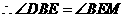 .
.
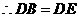 ,易得
,易得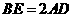 .得
.得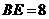 ;
;
②当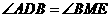 时,
时,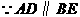 ,
,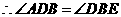 .
.
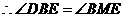 .又
.又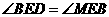 ,
,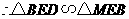 .
.
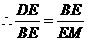 ,即
,即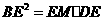 ,得
,得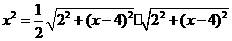 .
.
解得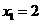 ,
,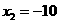 (舍去).即线段
(舍去).即线段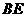 的长为2.
的长为2.
综上所述,所求线段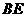 的长为8或2.
的长为8或2.
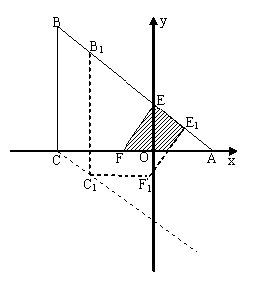
17、 (2008湖北荆州)如图,等腰直角三角形纸片ABC中,AC=BC=4,∠ACB=90º,直角边AC在x轴上,B点在第二象限,A(1,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在直线重合,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA平移,至B点到达A点停止.设平移时间为t(s),移动速度为每秒1个单位长度,平移中四边形BCFE与△AEF重叠的面积为S.
(2008湖北荆州)如图,等腰直角三角形纸片ABC中,AC=BC=4,∠ACB=90º,直角边AC在x轴上,B点在第二象限,A(1,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在直线重合,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA平移,至B点到达A点停止.设平移时间为t(s),移动速度为每秒1个单位长度,平移中四边形BCFE与△AEF重叠的面积为S.
(1)求折痕EF的长;
(2)是否存在某一时刻t使平移中直角顶点C经过抛物线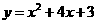 的顶点?若存在,求出t值;若不存在,请说明理由;
的顶点?若存在,求出t值;若不存在,请说明理由;
(3)直接写出S与t的函数关系式及自变量t的取值范围.
答案:


 ∥BA 交Y轴于P,
∥BA 交Y轴于P,

|

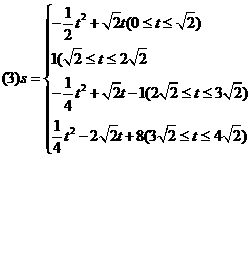
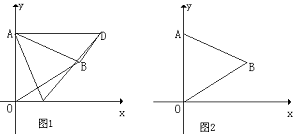
16、(2008浙江金华) 如图1,在平面直角坐标系中,己知ΔAOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连结AP,并把ΔAOP绕着点A按逆时针方向旋转.使边AO与AB重合.得到ΔABD.
(1)求直线AB的解析式;
(2)当点P运动到点(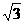 ,0)时,求此时DP的长及点D的坐标;
,0)时,求此时DP的长及点D的坐标;
(3)是否存在点P,使ΔOPD的面积等于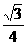 ,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由。
,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由。
答案:解:(1)作BE⊥OA,
∴ΔAOB是等边三角形
∴BE=OB·sin60o=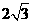 ,
,
∴B(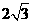 ,2)
,2)
∵A(0,4),设AB的解析式为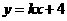 ,所以
,所以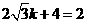 ,解得
,解得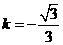 ,的以直线AB的解析式为
,的以直线AB的解析式为
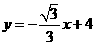
(2)由旋转知,AP=AD, ∠PAD=60o,
∴ΔAPD是等边三角形,PD=PA=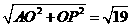
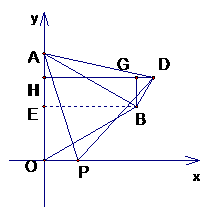
如图,作BE⊥AO,DH⊥OA,GB⊥DH,显然ΔGBD中∠GBD=30°
∴GD=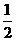 BD=
BD=
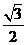 ,DH=GH+GD=
,DH=GH+GD=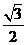 +
+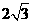 =
=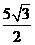 ,
,
∴GB=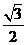 BD=
BD=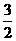 ,OH=OE+HE=OE+BG=
,OH=OE+HE=OE+BG=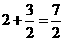
∴D(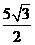 ,
,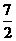 )
)
(3)设OP=x,则由(2)可得D(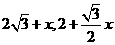 )
)
若ΔOPD的面积为: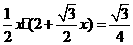
解得: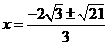
所以P(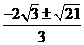 ,0)
,0)
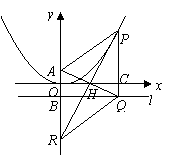
15、(2008江苏镇江)探索研究
如图,在直角坐标系 中,点
中,点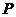 为函数
为函数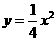 在第一象限内的图象上的任一点,点
在第一象限内的图象上的任一点,点 的坐标为
的坐标为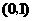 ,直线
,直线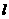 过
过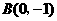 且与
且与 轴平行,过
轴平行,过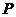 作
作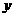 轴的平行线分别交
轴的平行线分别交 轴,
轴,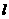 于
于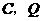 ,连结
,连结 交
交 轴于
轴于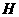 ,直线
,直线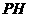 交
交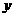 轴于
轴于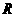 .
.
(1)求证: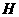 点为线段
点为线段 的中点;
的中点;
(2)求证:①四边形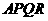 为平行四边形;
为平行四边形;
②平行四边形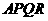 为菱形;
为菱形;
(3)除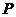 点外,直线
点外,直线 与抛物线
与抛物线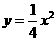 有无其它公共点?并说明理由.
有无其它公共点?并说明理由.

答案:
(1)法一:由题可知 .
.
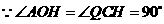 ,
,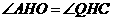 ,
,
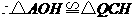 .
.
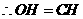 ,即
,即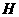 为
为 的中点.
的中点.
法二: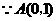 ,
,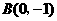 ,
,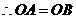 .
.
又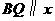 轴,
轴,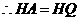 .
.
(2)①由(1)可知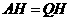 ,
,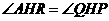 ,
,
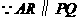 ,
,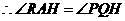 ,
,
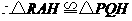 .
.
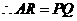 ,
,
又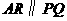 ,
, 四边形
四边形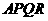 为平行四边形.
为平行四边形.
②设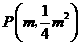 ,
,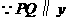 轴,则
轴,则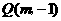 ,则
,则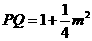 .
.
过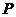 作
作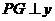 轴,垂足为
轴,垂足为 ,在
,在 中,
中,
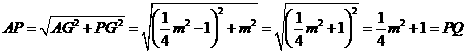 .
.
 平行四边形
平行四边形 为菱形.
为菱形.
(3)设直线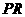 为
为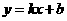 ,由
,由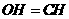 ,得
,得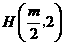 ,
,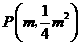 代入得:
代入得:
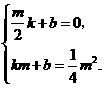
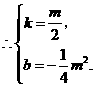
 直线
直线 为
为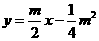 .
.
设直线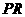 与抛物线的公共点为
与抛物线的公共点为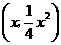 ,代入直线
,代入直线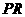 关系式得:
关系式得:
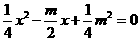 ,
,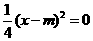 ,解得
,解得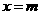 .得公共点为
.得公共点为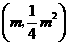 .
.
所以直线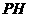 与抛物线
与抛物线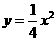 只有一个公共点
只有一个公共点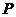 .
.
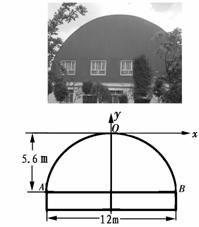
13、 (2008新疆建设兵团)某工厂要赶制一批抗震救灾用的大型活动板房.如图,板房一面
的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为5.6m.
(1)在如图所示的平面直角坐标系中,求抛物线的表达式.
(2)现需在抛物线AOB的区域内安装几扇窗户,窗户的底边在AB上,每扇窗户宽1.5m,高1.6m,相邻窗户之间的间距均为0.8m,左右两边窗户的窗角所在的点到抛物线的水平距离至少为0.8m.请计算最多可安装几扇这样的窗户?
答案:解:(1)设抛物线的表达式为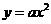
点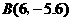 在抛物线的图象上.
在抛物线的图象上.
∴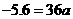
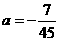
∴抛物线的表达式为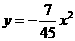
(2)设窗户上边所在直线交抛物线于C、D两点,D点坐标为(k,t)
已知窗户高1.6m,∴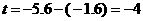
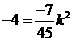
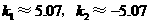 (舍去)
(舍去)
∴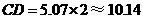 (m)
(m)
又设最多可安装n扇窗户
∴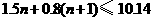
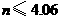 .
.
答:最多可安装4扇窗户.
(本题不要求学生画出4个表示窗户的小矩形)
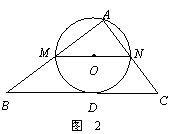
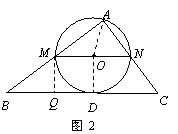
12、(2008山东东营、菏泽)在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?





答案:解:(1)∵MN∥BC,∴∠AMN=∠B,∠ANM=∠C.
 ∴ △AMN ∽ △ABC.
∴ △AMN ∽ △ABC.
∴ 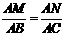 ,即
,即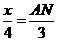 .
.
∴ AN=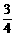 x.
x.
∴ 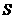 =
=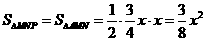 .(0<
.(0< <4)
<4)
(2)如图2,设直线BC与⊙O相切于点D,连结AO,OD,则AO =OD
=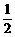 MN.
MN.

在Rt△ABC中,BC =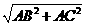 =5.
=5.
由(1)知 △AMN ∽ △ABC.
∴ 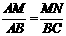 ,即
,即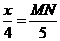 .
.
∴ 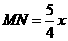 ,
,
∴ 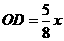 .
.
过M点作MQ⊥BC 于Q,则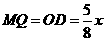 .
.
在Rt△BMQ与Rt△BCA中,∠B是公共角,
∴ △BMQ∽△BCA.
∴ 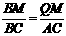 .
.
∴ 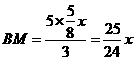 ,
,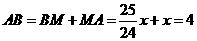 .
.
∴ x=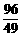 .
.
∴ 当x=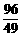 时,⊙O与直线BC相切.
时,⊙O与直线BC相切.
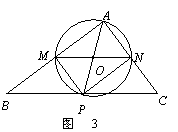 (3)随点M的运动,当P点落在直线BC上时,连结AP,则O点为AP的中点.
(3)随点M的运动,当P点落在直线BC上时,连结AP,则O点为AP的中点.
∵ MN∥BC,∴ ∠AMN=∠B,∠AOM=∠APC.
∴ △AMO ∽ △ABP.
∴ 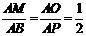 . AM=MB=2.
. AM=MB=2.
故以下分两种情况讨论:
① 当0< ≤2时,
≤2时,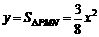 .
.
∴ 当 =2时,
=2时,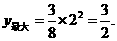
② 当2< <4时,设PM,PN分别交BC于E,F.
<4时,设PM,PN分别交BC于E,F.
 ∵ 四边形AMPN是矩形,
∵ 四边形AMPN是矩形,
∴ PN∥AM,PN=AM=x.
又∵ MN∥BC,
∴ 四边形MBFN是平行四边形.
∴ FN=BM=4-x.
∴ 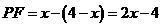 .
.
又△PEF ∽ △ACB.
∴ 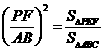 .
.
∴ 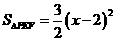 .
.
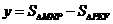 =
=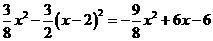 .
.
当2< <4时,
<4时,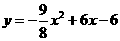
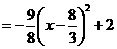 .
.
∴ 当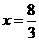 时,满足2<
时,满足2< <4,
<4,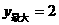 .
.
综上所述,当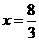 时,
时,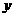 值最大,最大值是2.
值最大,最大值是2.
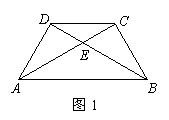
11、(2008广东中山)将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边
AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连结CD.
(1)填空:如图1,AC= ,BD= ;四边形ABCD是 梯形.
(2)请写出图9中所有的相似三角形(不含全等三角形).
(3)如图2若以AB所在直线为 轴,过点A垂直于AB的直线为
轴,过点A垂直于AB的直线为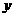 轴建立如图10的平面直角坐标系,保持ΔABD不动,将ΔABC向
轴建立如图10的平面直角坐标系,保持ΔABD不动,将ΔABC向 轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围.
轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围.

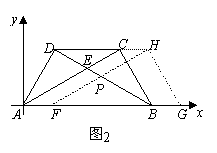

答案:解:(1)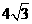 ,
,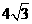 ,等腰;
,等腰;
(2)共有9对相似三角形.
①△DCE、△ABE与△ACD或△BDC两两相似,分别是:△DCE∽△ABE,△DCE∽△ACD,△DCE∽△BDC,△ABE∽△ACD,△ABE∽△BDC;(有5对)
②△ABD∽△EAD,△ABD∽△EBC;(有2对)
③△BAC∽△EAD,△BAC∽△EBC;(有2对)
所以,一共有9对相似三角形.
(3)由题意知,FP∥AE,
∴ ∠1=∠PFB,
又∵ ∠1=∠2=30°,
∴ ∠PFB=∠2=30°,
∴ FP=BP.
过点P作PK⊥FB于点K,则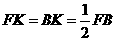 .
.
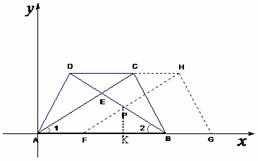
∵ AF=t,AB=8,
∴ FB=8-t,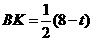 .
.
在Rt△BPK中,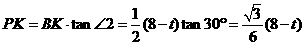 .
.
∴ △FBP的面积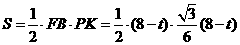 ,
,
∴ S与t之间的函数关系式为:
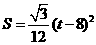 ,或
,或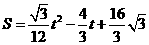 .
.
t的取值范围为: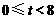 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com