
题目列表(包括答案和解析)
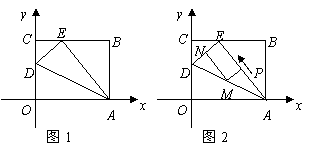
10、(2008甘肃兰州)如图1,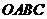 是一张放在平面直角坐标系中的矩形纸片,
是一张放在平面直角坐标系中的矩形纸片, 为原点,点
为原点,点 在
在 轴的正半轴上,点
轴的正半轴上,点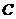 在
在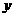 轴的正半轴上,
轴的正半轴上,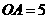 ,
,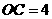 .
.
(1)在 边上取一点
边上取一点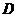 ,将纸片沿
,将纸片沿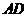 翻折,使点
翻折,使点 落在
落在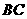 边上的点
边上的点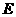 处,求
处,求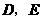 两点的坐标;
两点的坐标;
(2)如图2,若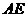 上有一动点
上有一动点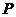 (不与
(不与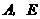 重合)自
重合)自 点沿
点沿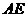 方向向
方向向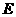 点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为
点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为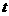 秒(
秒(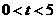 ),过
),过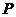 点作
点作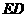 的平行线交
的平行线交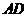 于点
于点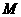 ,过点
,过点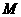 作
作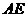 的平行线交
的平行线交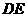 于点
于点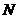 .求四边形
.求四边形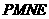 的面积
的面积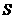 与时间
与时间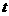 之间的函数关系式;当
之间的函数关系式;当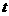 取何值时,
取何值时,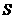 有最大值?最大值是多少?
有最大值?最大值是多少?
 (3)在(2)的条件下,当
(3)在(2)的条件下,当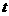 为何值时,以
为何值时,以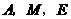 为顶点的三角形为等腰三角形,并求出相应的时刻点
为顶点的三角形为等腰三角形,并求出相应的时刻点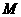 的坐标.
的坐标.
答案:解:(1)依题意可知,折痕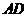 是四边形
是四边形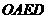 的对称轴,
的对称轴,
 在
在 中,
中,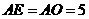 ,
,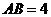 .
.
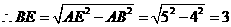 .
.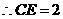 .
.
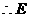 点坐标为(2,4).
点坐标为(2,4).
在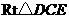 中,
中,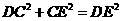 , 又
, 又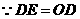 .
.
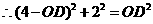 . 解得:
. 解得: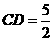 .
.
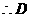 点坐标为
点坐标为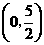
(2)如图①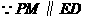 ,
,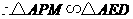 .
.
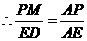 ,又知
,又知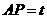 ,
,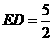 ,
,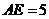
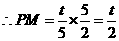 , 又
, 又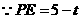 .
.
而显然四边形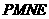 为矩形.
为矩形.
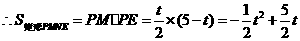
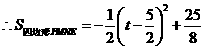 ,又
,又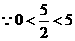
 当
当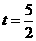 时,
时, 有最大值
有最大值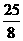 .
.
(3)(i)若以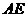 为等腰三角形的底,则
为等腰三角形的底,则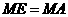 (如图①)
(如图①)
在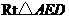 中,
中,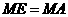 ,
,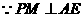 ,
,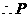 为
为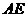 的中点,
的中点,

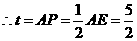 .
.
又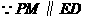 ,
,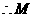 为
为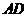 的中点.
的中点.
过点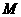 作
作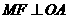 ,垂足为
,垂足为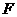 ,则
,则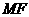 是
是 的中位线,
的中位线,
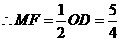 ,
,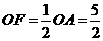 ,
,
 当
当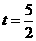 时,
时,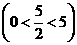 ,
,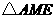 为等腰三角形.
为等腰三角形.
此时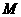 点坐标为
点坐标为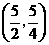 .
.
(ii)若以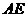 为等腰三角形的腰,则
为等腰三角形的腰,则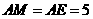 (如图②)
(如图②)
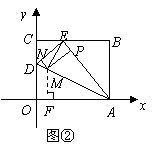 在
在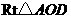 中,
中,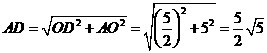 .
.
过点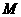 作
作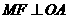 ,垂足为
,垂足为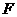 .
.
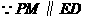 ,
,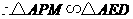 .
.
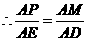 .
.
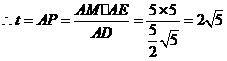 ,
,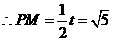 .
.
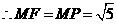 ,
,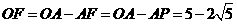 ,
,
 当
当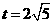 时,(
时,(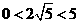 ),此时
),此时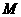 点坐标为
点坐标为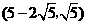 .
.
综合(i)(ii)可知,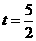 或
或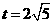 时,以
时,以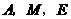 为顶点的三角形为等腰三角形,相应
为顶点的三角形为等腰三角形,相应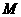 点的坐标为
点的坐标为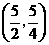 或
或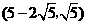 .
.
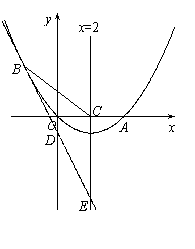
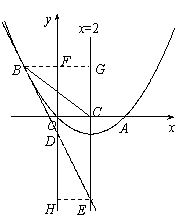
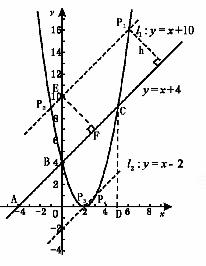
9、(2008海南)如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2 与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.
(1)求m的值及该抛物线对应的函数关系式;
(2)求证:① CB=CE ;② D是BE的中点;
(3)若P(x,y)是该抛物线上的一个动点,是否存在这样的点P,使得PB=PE,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由

答案:解:(1)∵ 点B(-2,m)在直线y=-2x-1上,
∴m=-2×(-2)-1=3. ∴ B(-2,3)
∵ 抛物线经过原点O和点A,对称轴为x=2,
∴ 点A的坐标为(4,0) .
设所求的抛物线对应函数关系式为y=a(x-0)(x-4).
将点B(-2,3)代入上式,得3=a(-2-0)(-2-4),∴ 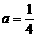 .
.
∴ 所求的抛物线对应的函数关系式为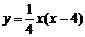 ,即
,即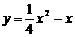 .
.
(2)①直线y=-2x-1与y轴、直线x=2的交点坐标分别为D(0,-1) E(2,-5).
过点B作BG∥x轴,与y轴交于F、直线x=2交于G,
则BG⊥直线x=2,BG=4.
在Rt△BGC中,BC=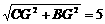 .
.
∵ CE=5,
 ∴ CB=CE=5.
∴ CB=CE=5.
②过点E作EH∥x轴,交y轴于H,
则点H的坐标为H(0,-5).
又点F、D的坐标为F(0,3)、D(0,-1),
∴ FD=DH=4,BF=EH=2,∠BFD=∠EHD=90°.
∴ △DFB≌△DHE (SAS),
∴ BD=DE.
即D是BE的中点.
(3)存在.
由于PB=PE,∴ 点P在直线CD上,
∴ 符合条件的点P是直线CD与该抛物线的交点.
设直线CD对应的函数关系式为y=kx+b.
将D(0,-1) C(2,0)代入,得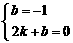 . 解得
. 解得 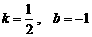 .
.
∴ 直线CD对应的函数关系式为y=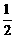 x-1.
x-1.
∵ 动点P的坐标为(x,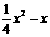 ),
),
∴ 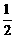 x-1=
x-1=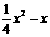 .
.
解得 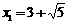 ,
,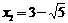 . ∴
. ∴ 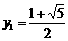 ,
,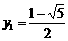 .
.
∴ 符合条件的点P的坐标为(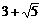 ,
,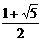 )或(
)或(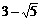 ,
,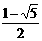 ).
).
8、(2008四川自贡)抛物线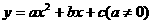 的顶点为M,与
的顶点为M,与 轴的交点为A、B(点
轴的交点为A、B(点
B在点A的右侧),△ABM的三个内角∠M、∠A、∠B所对的边分别为m、a、b.若关
于 的一元二次方程
的一元二次方程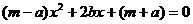 有两个相等的实数根.
有两个相等的实数根.
(1)判断△ABM的形状,并说明理由.
(2)当顶点M的坐标为(-2,-1)时,求抛物线的解析式,并画出该抛物线的大致图形.
(3)若平行于 轴的直线与抛物线交于C、D两点,以CD为直径的圆恰好与
轴的直线与抛物线交于C、D两点,以CD为直径的圆恰好与 轴相切,求该圆的圆心坐标.
轴相切,求该圆的圆心坐标.
答案:解:(1)令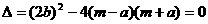 ,得
,得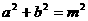
由勾股定理的逆定理和抛物线的对称性知△ABM是一个以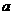 、
、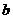 为直角边的等腰直角三角形
为直角边的等腰直角三角形
(2)设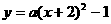
∵△ABM是等腰直角三角形
∴斜边上的中线等于斜边的一半
又顶点M(-2,-1)
∴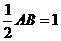 ,即AB=2
,即AB=2
∴A(-3,0),B(-1,0)
将B(-1,0) 代入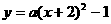 中得
中得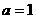
∴抛物线的解析式为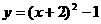 ,即
,即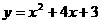
图略
(3)设平行于 轴的直线为
轴的直线为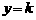
解方程组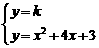
得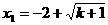 ,
,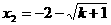 (
(
∴线段CD的长为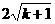
∵以CD为直径的圆与 轴相切
轴相切
据题意得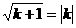
∴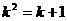
解得 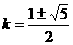
∴圆心坐标为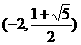 和
和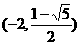
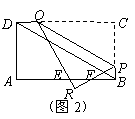
7、(2008浙江台州)如图,在矩形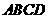 中,
中,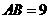 ,
,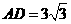 ,点
,点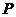 是边
是边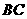 上的动点(点
上的动点(点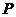 不与点
不与点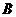 ,点
,点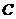 重合),过点
重合),过点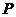 作直线
作直线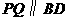 ,交
,交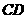 边于
边于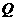 点,再把
点,再把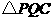 沿着动直线
沿着动直线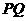 对折,点
对折,点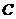 的对应点是
的对应点是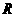 点,设
点,设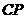 的长度为
的长度为 ,
,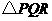 与矩形
与矩形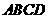 重叠部分的面积为
重叠部分的面积为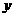 .
.
(1)求 的度数;
的度数;
(2)当 取何值时,点
取何值时,点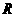 落在矩形
落在矩形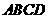 的
的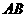 边上?
边上?
(3)①求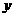 与
与 之间的函数关系式;
之间的函数关系式;
②当 取何值时,重叠部分的面积等于矩形面积的
取何值时,重叠部分的面积等于矩形面积的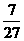 ?
?
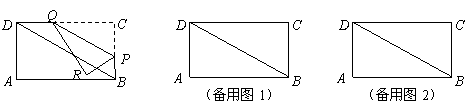

答案:解:(1)如图, 四边形
四边形 是矩形,
是矩形, .
.
又 ,
,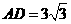 ,
,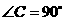 ,
,
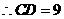 ,
,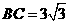 .
.
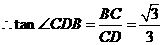 ,
,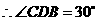 .
.
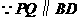 ,
,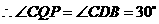 .
.
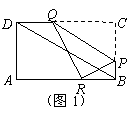 (2)如图1,由轴对称的性质可知,
(2)如图1,由轴对称的性质可知,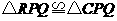 ,
,
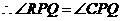 ,
,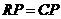 .
.
由(1)知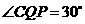 ,
,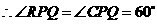 ,
,
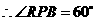 ,
,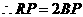 .
.
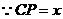 ,
,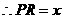 ,
,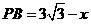 .
.
在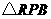 中,根据题意得:
中,根据题意得: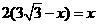 ,
,
解这个方程得: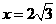 .
.
(3)①当点 在矩形
在矩形 的内部或
的内部或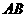 边上时,
边上时,
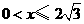 ,
,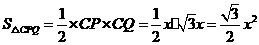 ,
,
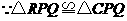 ,
, 当
当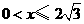 时,
时,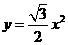
当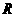 在矩形
在矩形 的外部时(如图2),
的外部时(如图2),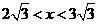 ,
,
 在
在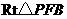 中,
中,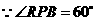 ,
,
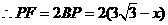 ,
,
又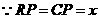 ,
,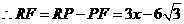 ,
,
在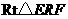 中,
中,
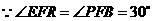 ,
,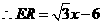 .
.
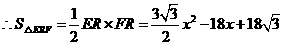 ,
,
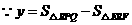 ,
,
 当
当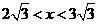 时,
时,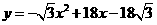 .
.
综上所述,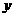 与
与 之间的函数解析式是:
之间的函数解析式是: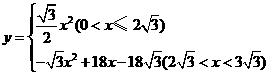 .
.
②矩形面积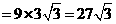 ,当
,当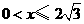 时,函数
时,函数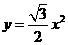 随自变量的增大而增大,所以
随自变量的增大而增大,所以 的最大值是
的最大值是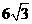 ,而矩形面积的
,而矩形面积的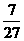 的值
的值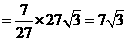 ,
,
而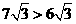 ,所以,当
,所以,当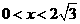 时,
时,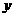 的值不可能是矩形面积的
的值不可能是矩形面积的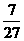 ;
;
当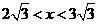 时,根据题意,得:
时,根据题意,得:
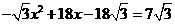 ,解这个方程,得
,解这个方程,得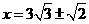 ,因为
,因为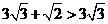 ,
,
所以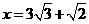 不合题意,舍去.
不合题意,舍去.
所以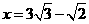 .
.
综上所述,当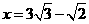 时,
时,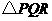 与矩形
与矩形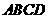 重叠部分的面积等于矩形面积的
重叠部分的面积等于矩形面积的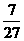 .
.
6、 (2008山东烟台)如图,抛物线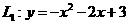 交
交 轴于A、B两点,交
轴于A、B两点,交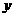 轴于M点.抛物线
轴于M点.抛物线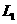 向右平移2个单位后得到抛物线
向右平移2个单位后得到抛物线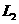 ,
,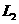 交
交 轴于C、D两点.
轴于C、D两点.
(1)求抛物线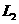 对应的函数表达式;
对应的函数表达式;
(2)抛物线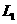 或
或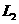 在
在 轴上方的部分是否存在点N,使以A,C,M,N为顶点的四边形是平行四边形.若存在,求出点N的坐标;若不存在,请说明理由;
轴上方的部分是否存在点N,使以A,C,M,N为顶点的四边形是平行四边形.若存在,求出点N的坐标;若不存在,请说明理由;
(3)若点P是抛物线 上的一个动点(P不与点A、B重合),那么点P关于原点的对称点Q是否在抛物线
上的一个动点(P不与点A、B重合),那么点P关于原点的对称点Q是否在抛物线 上,请说明理由.
上,请说明理由.
答案:



5、(2008安徽芜湖)如图,已知 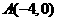 ,
,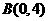 ,现以A点为位似中心,相似比为9:4,将OB向右侧放大,B点的对应点为C.
,现以A点为位似中心,相似比为9:4,将OB向右侧放大,B点的对应点为C.
(1)求C点坐标及直线BC的解析式;
(2)一抛物线经过B、C两点,且顶点落在x轴正半轴上,求该抛物线的解析式并画出函数图象;
(3)现将直线BC绕B点旋转与抛物线相交与另一点P,请找出抛物线上所有满足到直线AB距离为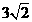 的点P.
的点P.
答案:解:
(1)过C点向x轴作垂线,垂足为D,由位似图形性质可知:
△ABO∽△ACD, ∴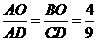 .
.
由已知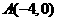 ,
,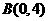 可知:
可知: 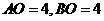 .
.
∴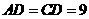 .∴C点坐标为
.∴C点坐标为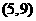 .
.
直线BC的解析是为: 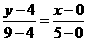
化简得: 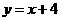
(2)设抛物线解析式为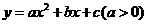 ,由题意得:
,由题意得: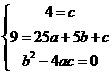 ,
,
解得: 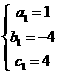
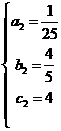
∴解得抛物线解析式为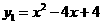 或
或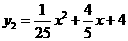 .
.
又∵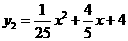 的顶点在x轴负半轴上,不合题意,故舍去.
的顶点在x轴负半轴上,不合题意,故舍去.
∴满足条件的抛物线解析式为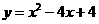
(准确画出函数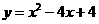 图象)
图象)
(3) 将直线BC绕B点旋转与抛物线相交与另一点P,设P到 直线AB的距离为h,
故P点应在与直线AB平行,且相距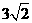 的上下两条平行直线
的上下两条平行直线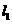 和
和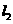 上.
上.
由平行线的性质可得:两条平行直线与y轴的交点到直线BC的距离也为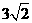 .
.
如图,设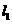 与y轴交于E点,过E作EF⊥BC于F点,
与y轴交于E点,过E作EF⊥BC于F点,
在Rt△BEF中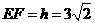 ,
,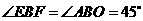 ,
,
∴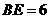 .∴可以求得直线
.∴可以求得直线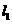 与y轴交点坐标为
与y轴交点坐标为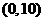
同理可求得直线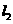 与y轴交点坐标为
与y轴交点坐标为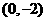
∴两直线解析式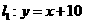 ;
;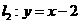 .
.
根据题意列出方程组: ⑴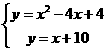 ;⑵
;⑵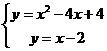
∴解得: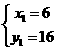 ;
;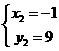 ;
;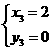 ;
;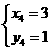
∴满足条件的点P有四个,它们分别是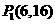 ,
,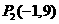 ,
,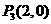 ,
,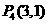 .
.
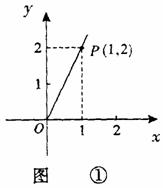
4、(2008广西南宁)随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高。某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润 与投资量
与投资量 成正比例关系,如图①所示;种植花卉的利润
成正比例关系,如图①所示;种植花卉的利润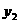 与投资量
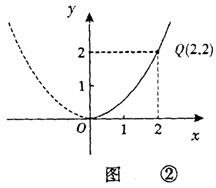
与投资量 成二次函数关系,如图②所示(注:利润与投资量的单位:万元)
成二次函数关系,如图②所示(注:利润与投资量的单位:万元)
(1)分别求出利润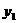 与
与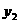 关于投资量
关于投资量 的函数关系式;
的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
(注意:在试题卷上作答无效)
答案:解:(1)设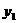 =
=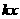 ,由图①所示,函数
,由图①所示,函数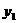 =
=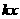 的图像过(1,2),所以2=
的图像过(1,2),所以2=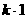 ,
,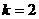
故利润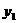 关于投资量
关于投资量 的函数关系式是
的函数关系式是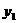 =
=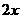 ;
;
因为该抛物线的顶点是原点,所以设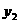 =
=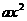 ,由图12-②所示,函数
,由图12-②所示,函数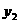 =
=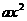 的图像过(2,2),
的图像过(2,2),
所以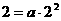 ,
,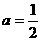
故利润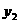 关于投资量
关于投资量 的函数关系式是
的函数关系式是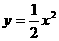 ;
;
(2)设这位专业户投入种植花卉 万元(
万元(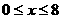 ),
),
则投入种植树木(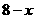 )万元,他获得的利润是
)万元,他获得的利润是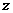 万元,根据题意,得
万元,根据题意,得
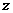 =
=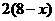 +
+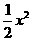 =
=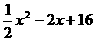 =
=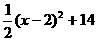
当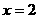 时,
时,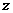 的最小值是14;
的最小值是14;
因为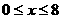 ,所以
,所以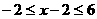
所以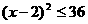
所以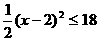
所以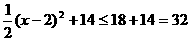 ,即
,即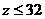 ,此时
,此时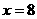
当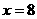 时,
时,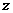 的最大值是32.
的最大值是32.
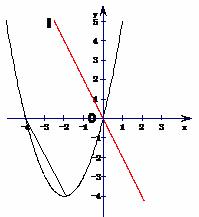
3、(2008江苏常州)如图,抛物线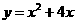 与x轴分别相交于点B、O,它的顶点为A,连接AB,把AB所的直线沿y轴向上平移,使它经过原点O,得到直线l,设P是直线l上一动点.
与x轴分别相交于点B、O,它的顶点为A,连接AB,把AB所的直线沿y轴向上平移,使它经过原点O,得到直线l,设P是直线l上一动点.
(1)求点A的坐标;
(2)以点A、B、O、P为顶点的四边形中,有菱形、等腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P的坐标;
(3)设以点A、B、O、P为顶点的四边形的面积为S,点P的横坐标为x,当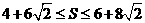 时,求x的取值范围.
时,求x的取值范围.
答案:解:(1)∵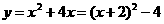
∴A(-2,-4)
(2)四边形ABP1O为菱形时,P1(-2,4)
四边形ABOP2为等腰梯形时,P1(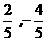 )
)
四边形ABP3O为直角梯形时,P1(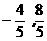 )
)
四边形ABOP4为直角梯形时,P1(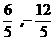 )
)
(3)
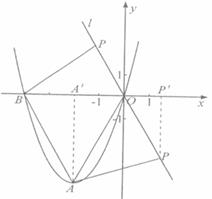
由已知条件可求得AB所在直线的函数关系式是y=-2x-8,所以直线 的函数关系式是y=-2x
的函数关系式是y=-2x
①当点P在第二象限时,x<0,
△POB的面积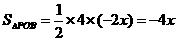
∵△AOB的面积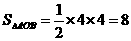 ,
,
∴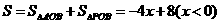
∵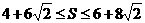 ,
,
∴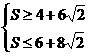
即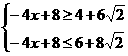 ∴
∴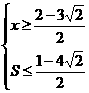
∴x的取值范围是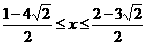
②当点P在第四象限是,x>0,
过点A、P分别作x轴的垂线,垂足为A′、P′
则四边形POA′A的面积
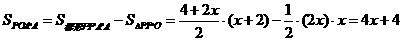
∵△AA′B的面积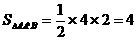
∴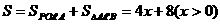
∵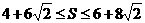 ,
,
∴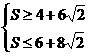 即
即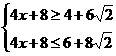 ∴
∴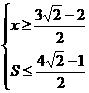
∴x的取值范围是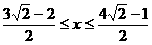
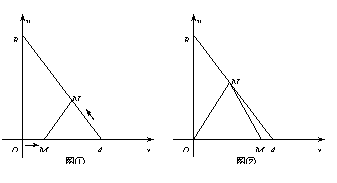
2、(2008 湖北 天门)如图①,在平面直角坐标系中,A点坐标为(3,0),B点坐标为(0,4).动点M从点O出发,沿OA方向以每秒1个单位长度的速度向终点A运动;同时,动点N从点A出发沿AB方向以每秒 个单位长度的速度向终点B运动.设运动了x秒.
个单位长度的速度向终点B运动.设运动了x秒.
(1)点N的坐标为(________________,________________);(用含x的代数式表示)
(2)当x为何值时,△AMN为等腰三角形?
(3)如图②,连结ON得△OMN,△OMN可能为正三角形吗?若不能,点M的运动速度不变,试改变点N的运动速度,使△OMN为正三角形,并求出点N的运动速度和此时x的值.

答案:解:(1)N(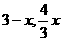 )
)
(2)①AM=AN
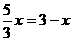 ,
,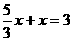 ,
,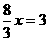 ,
,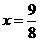
②MN=AM
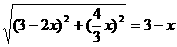
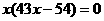
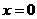 (舍去)或
(舍去)或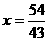
③MN=AN
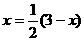 ,
,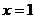
(3)不能
当N(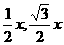 )时,△OMN为正三角形
)时,△OMN为正三角形
由题意可得: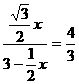 ,解得:
,解得: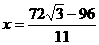
点N的速度为: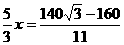
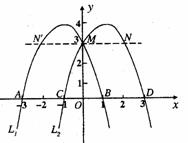
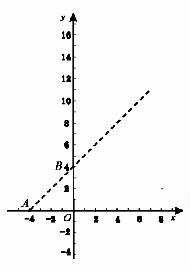
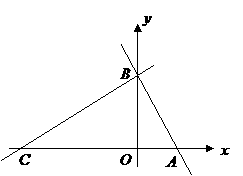
1、如图,在平面直角坐标系中,点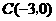 ,点
,点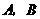 分别在
分别在 轴,
轴,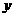 轴的正半轴上,且满足
轴的正半轴上,且满足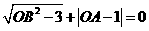 .
.
(1)求点 ,点
,点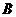 的坐标.
的坐标.
(2)若点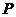 从
从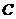 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线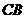 运动,连结
运动,连结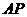 .设
.设 的面积为
的面积为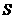 ,点
,点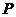 的运动时间为
的运动时间为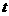 秒,求
秒,求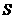 与
与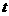 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点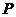 ,使以点
,使以点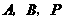 为顶点的三角形与
为顶点的三角形与 相似?若存在,请直接写出点
相似?若存在,请直接写出点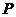 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
答案:解:(1)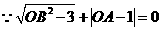
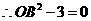 ,
,
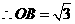 ,
,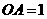
 点
点 ,点
,点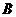 分别在
分别在 轴,
轴,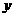 轴的正半轴上
轴的正半轴上
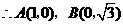
(2)求得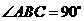
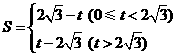
(每个解析式各1分,两个取值范围共1分)
(3)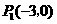 ;
;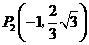 ;
;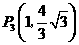 ;
;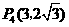
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com