
题目列表(包括答案和解析)
24. (10分)解:(1)设抛物线的表达式为
(10分)解:(1)设抛物线的表达式为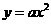 1分
1分
点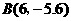 在抛物线的图象上.
在抛物线的图象上.
∴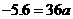
 ······························································ 3分
······························································ 3分
∴抛物线的表达式为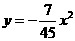 ············································································· 4分
············································································· 4分
(2)设窗户上边所在直线交抛物线于C、D两点,D点坐标为(k,t)
已知窗户高1.6m,∴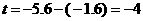 ··························································· 5分
··························································· 5分
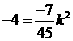
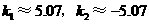 (舍去)············································································ 6分
(舍去)············································································ 6分
∴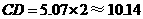 (m)·············································································· 7分
(m)·············································································· 7分
又设最多可安装n扇窗户
∴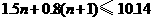 ····················································································· 9分
····················································································· 9分
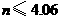 .
.
答:最多可安装4扇窗户.···················································································· 10分
(本题不要求学生画出4个表示窗户的小矩形)
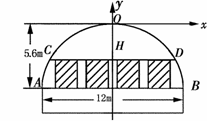
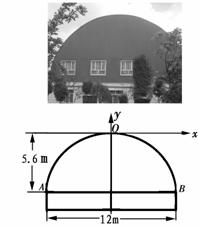
91.(10分)某工厂要赶制一批抗震救灾用的大型活动板房.如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为5.6m.
(1)在如图所示的平面直角坐标系中,求抛物线的表达式.
(2)现需在抛物线AOB的区域内安装几扇窗户,窗户的底边在AB上,每扇窗户宽1.5m,高1.6m,相邻窗户之间的间距均为0.8m,左右两边窗户的窗角所在的点到抛物线的水平距离至少为0.8m.请计算最多可安装几扇这样的窗户?
106.(08四川乐山28题)28.如图(18),在平面直角坐标系中, 的边
的边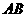 在
在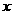 轴上,且
轴上,且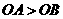 ,以
,以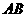 为直径的圆过点
为直径的圆过点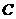 .若点
.若点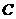 的坐标为
的坐标为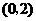 ,
,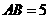 ,A、B两点的横坐标
,A、B两点的横坐标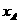 ,
,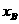 是关于
是关于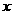 的方程
的方程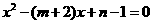 的两根.
的两根.
(1)求 、
、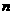 的值;
的值;
(2)若 平分线所在的直线
平分线所在的直线 交
交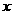 轴于点
轴于点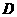 ,试求直线
,试求直线 对应的一次函数解析式;
对应的一次函数解析式;
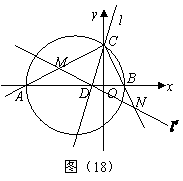 (3)过点
(3)过点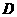 任作一直线
任作一直线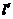 分别交射线
分别交射线 、
、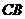 (点
(点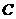 除外)于点
除外)于点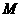 、
、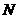 .则
.则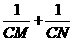 的是否为定值?若是,求出该定值;若不是,请说明理由.
的是否为定值?若是,求出该定值;若不是,请说明理由.
(08四川乐山28题解析)28.解:(1) 以
以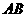 为直径的圆过点
为直径的圆过点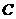 ,
,
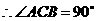 ,而点
,而点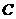 的坐标为
的坐标为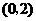 ,
,
由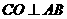 易知
易知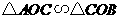 ,
,
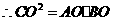 ,····································································································· 1分
,····································································································· 1分
即: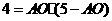 ,解之得:
,解之得: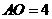 或
或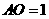 .
.
 ,
,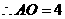 ,
,
即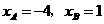 .···································································································· 2分
.···································································································· 2分
由根与系数关系有:
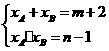 ,
,
解之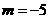 ,
,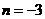 .································································································ 4分
.································································································ 4分
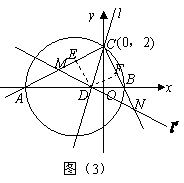 (2)如图(3),过点
(2)如图(3),过点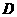 作
作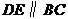 ,交
,交 于点
于点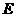 ,
,
易知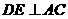 ,且
,且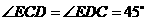 ,
,
在 中,易得
中,易得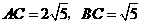 ,··········· 5分
,··········· 5分
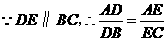 ,
,
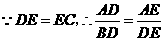 ,
,
又 ,有
,有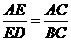 ,
,
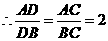 ,······································································································· 6分
,······································································································· 6分
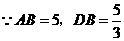 ,
,
则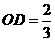 ,即
,即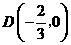 ,························································································ 7分
,························································································ 7分
易求得直线 对应的一次函数解析式为:
对应的一次函数解析式为: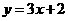 .··················································· 8分
.··················································· 8分
解法二:过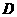 作
作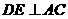 于
于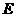 ,
,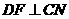 于
于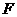 ,
,
由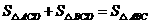 ,
,
求得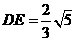 .········································································································ 5分
.········································································································ 5分
又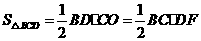 ,
,
求得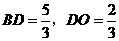 .····························································································· 7分
.····························································································· 7分
即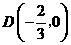 ,
,
易求得直线 对应的一次函数解析式为:
对应的一次函数解析式为: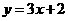 .··················································· 8分
.··················································· 8分
(3)过点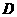 作
作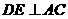 于
于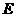 ,
,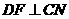 于
于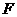 .
.
 为
为 的平分线,
的平分线,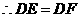 .
.
由 ,有
,有 ········································································· 9分
········································································· 9分
由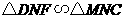 ,有
,有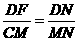 ······································································ 10分
······································································ 10分
 ,··············································································· 11分
,··············································································· 11分
即 .···················································································· 12分
.···················································································· 12分
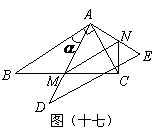
105.(08湖南邵阳25题)25.如图(十七),将含 角的直角三角板
角的直角三角板 (
(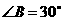 )绕其直角顶点
)绕其直角顶点 逆时针旋转
逆时针旋转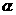 解(
解(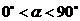 ),得到
),得到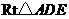 ,
,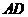 与
与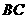 相交于点
相交于点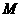 ,过点
,过点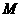 作
作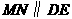 交
交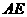 于点
于点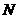 ,连结
,连结 .设
.设 ,
,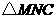 的面积为
的面积为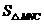 ,
, 的面积为
的面积为 .
.
 (1)求证:
(1)求证: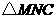 是直角三角形;
是直角三角形;
(2)试求用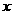 表示
表示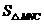 的函数关系式,并写出
的函数关系式,并写出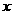 的取值范围;
的取值范围;
(3)以点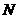 为圆心,
为圆心, 为半径作
为半径作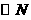 ,
,
①当直线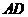 与
与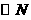 相切时,试探求
相切时,试探求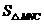 与
与 之间的关系;
之间的关系;
②当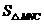
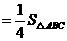 时,试判断直线
时,试判断直线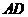 与
与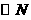 的位置关系,并说明理由.
的位置关系,并说明理由.
(08湖南邵阳25题解析)25. (1)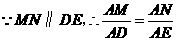 ,
,
又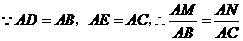 ,································································· 1分
,································································· 1分
又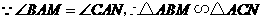 ,···························································· 2分
,···························································· 2分
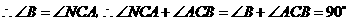 ,
,
 ,即
,即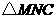 是直角三角形;······························································ 3分
是直角三角形;······························································ 3分
(2)在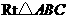 中,
中,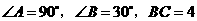 ,
,
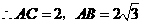 ,
,
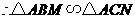 ,
,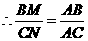 ,
,
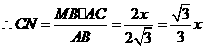 ;··············································································· 4分
;··············································································· 4分
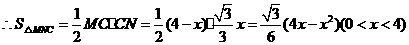 ;··························· 5分
;··························· 5分
(3)①直线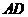 与
与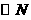 相切时,则
相切时,则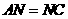 .
.
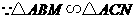 ,
,
 .
.
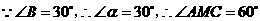 ,································································· 6分
,································································· 6分
又 ,
,
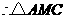 是等边三角形,
是等边三角形,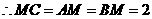 ,
,
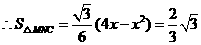 ,
,
又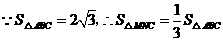 ;······································································ 7分
;······································································ 7分
②当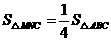 时,
时,
则有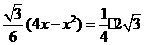 ,解之得
,解之得 或
或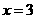 ;··················································· 8分
;··················································· 8分
(i)当 时,
时, ,
,
在 中,
中,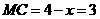 ,
,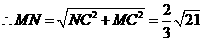 ,
,
在 中,
中,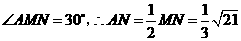 ,········································· 9分
,········································· 9分
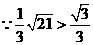 ,即
,即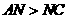 ,
,
 直线
直线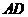 与
与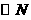 相离;···························································································· 10分
相离;···························································································· 10分
(ii)当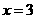 时,
时,
同理可求出: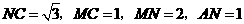 ,·············································· 11分
,·············································· 11分
 ,
,
 直线
直线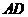 与
与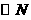 相交.···························································································· 12分
相交.···························································································· 12分
104.(08贵州遵义27题)27。(14分)如图(1)所示,一张平行四边形纸片ABCD,AB=10,AD=6,BD=8,沿对角线BD把这张纸片剪成△AB1D1和△CB2D2两个三角形(如图(2)所示),将△AB1D1沿直线AB1方向移动(点B2始终在AB1上,AB1与CD2始终保持平行),当点A与B2重合时停止平移,在平移过程中,AD1与B2D2交于点E,B2C与B1D1交于点F,
(1)当△AB1D1平移到图(3)的位置时,试判断四边形B2FD1E是什么四边形?并证明你的结论;
(2)设平移距离B2B1为x,四边形B2FD1E的面积为y,求y与x的函数关系式;并求出四边形B2FD1E的面积的最大值;
(3)连结B1C(请在图(3)中画出)。当平移距离B2B1的值是多少时,△ B1B2F与△ B1CF相似?

(08贵州遵义27题解析)解:(1) 四边形B2FD1E是矩形。
因为△AB1D1平移到图(3)的,所以四边形B2FD1E是一个平行四边形,又因为在平行四边形ABCD中,AB=10,AD=6,BD=8,则有∠ADB是直角。所以四边形B2FD1E是矩形。
(2)因为三角形B1B2F与三角形AB1D1相似,则有B2F=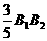 =0.6X,B1F=
=0.6X,B1F=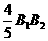 =0.8x
=0.8x
所以sB2FD1E=B2F×D1F=0.6X × (8-0.8x)=4.8x-0.48x2
即y=4.8x-0.48x2=12-0.48(x-5)
当x=5时,y=12是最大的值。
(3)要使△ B1B2F与△ B1CF相似,则有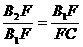 即
即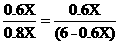
解之得:x=3.6
103.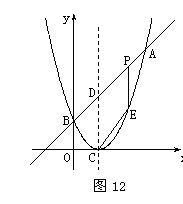 (08云南省卷24题) 24.(本大题满分14分)如图12,已知二次函数图象的顶点坐标为C(1,0),直线
(08云南省卷24题) 24.(本大题满分14分)如图12,已知二次函数图象的顶点坐标为C(1,0),直线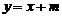 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴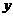 上.
上.
(1)求 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作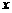 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为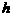 ,点P的横坐标为
,点P的横坐标为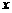 ,求
,求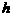 与
与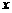 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量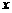 的取值范围;
的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
(08云南省卷24题解析) (1) ∵ 点A(3,4)在直线y=x+m上,
∴ 4=3+m. ………………………………(1分)
∴ m=1. ………………………………(2分)
设所求二次函数的关系式为y=a(x-1)2. ………………………………(3分)
∵ 点A(3,4)在二次函数y=a(x-1)2的图象上,
∴ 4=a(3-1)2,
∴ a=1. ………………………………(4分)
∴ 所求二次函数的关系式为y=(x-1)2.
即y=x2-2x+1. ………………………………(5分)
(2) 设P、E两点的纵坐标分别为yP和yE .
∴ PE=h=yP-yE ………………………………(6分)
=(x+1)-(x2-2x+1) ………………………………(7分)
=-x2+3x. ………………………………(8分)
即h=-x2+3x (0<x<3). ………………………………(9分)
(3) 存在. ………………………………(10分)
解法1:要使四边形DCEP是平行四边形,必需有PE=DC. …………………(11分)
∵ 点D在直线y=x+1上,
∴ 点D的坐标为(1,2),
∴ -x2+3x=2 .
即x2-3x+2=0 . ………………………………(12分)
解之,得 x1=2,x2=1 (不合题意,舍去) ………………………………(13分)
∴ 当P点的坐标为(2,3)时,四边形DCEP是平行四边形. ……………(14分)
解法2:要使四边形DCEP是平行四边形,必需有BP∥CE. ………………(11分)
设直线CE的函数关系式为y=x+b.
∵ 直线CE 经过点C(1,0),
∴ 0=1+b,
∴ b=-1 .
∴ 直线CE的函数关系式为y=x-1 .
∴  得x2-3x+2=0.
………………………………(12分)
得x2-3x+2=0.
………………………………(12分)
解之,得 x1=2,x2=1 (不合题意,舍去) ………………………………(13分)
∴ 当P点的坐标为(2,3)时,四边形DCEP是平行四边形. ……………(14分)
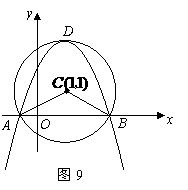
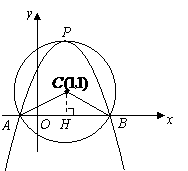
102.23.如图9,在平面直角坐标系中,以点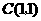 为圆心,2为半径作圆,交
为圆心,2为半径作圆,交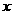 轴于
轴于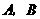 两点,开口向下的抛物线经过点
两点,开口向下的抛物线经过点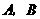 ,且其顶点
,且其顶点 在
在 上.
上.
 (1)求
(1)求 的大小;
的大小;
(2)写出 两点的坐标;
两点的坐标;
(3)试确定此抛物线的解析式;
(4)在该抛物线上是否存在一点 ,使线段
,使线段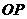 与
与 互相平分?若存在,求出点
互相平分?若存在,求出点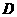 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 (08新疆乌鲁木齐23题解答)23.解:(1)作
(08新疆乌鲁木齐23题解答)23.解:(1)作 轴,
轴,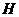 为垂足,
为垂足,
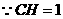 ,半径
,半径 ······················································ 1分
······················································ 1分
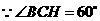 ,
,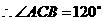 ······································ 3分
······································ 3分
(2)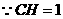 ,半径
,半径
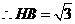 ,故
,故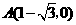 ,············································ 5分
,············································ 5分
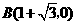 ········································································· 6分
········································································· 6分
(3)由圆与抛物线的对称性可知抛物线的顶点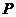 的坐标为
的坐标为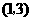 ··································· 7分
··································· 7分
设抛物线解析式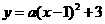 ·················································································· 8分
·················································································· 8分
把点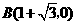 代入上式,解得
代入上式,解得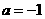 ······································································· 9分
······································································· 9分
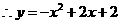 ····································································································· 10分
····································································································· 10分
(4)假设存在点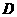 使线段
使线段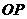 与
与 互相平分,则四边形
互相平分,则四边形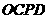 是平行四边形········· 11分
是平行四边形········· 11分
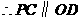 且
且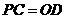 .
.
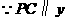 轴,
轴, 点
点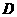 在
在 轴上.·············································································· 12分
轴上.·············································································· 12分
又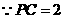 ,
,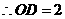 ,即
,即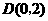 .
.
又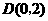 满足
满足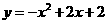 ,
,
 点
点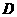 在抛物线上······································································································ 13分
在抛物线上······································································································ 13分
所以存在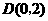 使线段
使线段 与
与 互相平分.···························································· 14分
互相平分.···························································· 14分
21.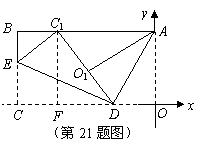 解:(1)过
解:(1)过 作
作 轴于点
轴于点 ,如图(第21题图)
,如图(第21题图)
在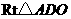 中,
中,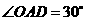 ,
,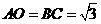
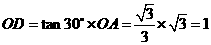 ································· 1分
································· 1分
由对称性可知: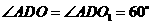
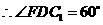
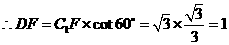 ············································································ 2分
············································································ 2分
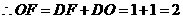
 点
点 的坐标为
的坐标为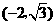 ····························································································· 3分
····························································································· 3分
(2)设经过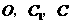 的抛物线的解析式为
的抛物线的解析式为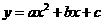 ,则
,则
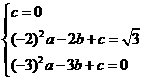 ································································································· 4分
································································································· 4分
解之得
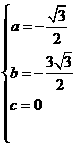
 抛物线的解析式为:
抛物线的解析式为: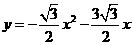 ································································· 5分
································································· 5分
(3)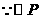 与两坐标轴相切
与两坐标轴相切
 圆心
圆心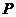 应在第一、三象限或第二、四象限的角平分线上.
应在第一、三象限或第二、四象限的角平分线上.
即在直线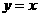 或
或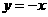 上·························································································· 6分
上·························································································· 6分
若点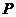 在直线
在直线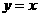 上,根据题意有
上,根据题意有
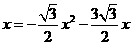
解之得
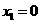 ,
,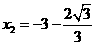
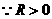

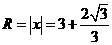 ····································································································· 7分
····································································································· 7分
若点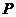 在直线
在直线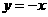 上,根据题意有
上,根据题意有
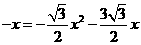
解之得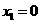 ,
,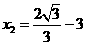
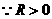
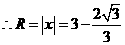
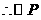 的半径
的半径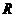 为
为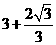 或
或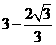 .······································································ 8分
.······································································ 8分
101.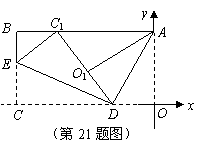 21.如图,已知平面直角坐标系中,有一矩形纸片
21.如图,已知平面直角坐标系中,有一矩形纸片 ,
, 为坐标原点,
为坐标原点, 轴,
轴, ,现将纸片按如图折叠,
,现将纸片按如图折叠,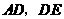 为折痕,
为折痕,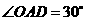 .折叠后,点
.折叠后,点 落在点
落在点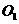 ,点
,点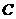 落在线段
落在线段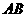 上的
上的 处,并且
处,并且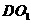 与
与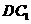 在同一直线上.
在同一直线上.
(1)求 的坐标;
的坐标;
(2)求经过三点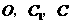 的抛物线的解析式;
的抛物线的解析式;
(3)若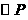 的半径为
的半径为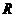 ,圆心
,圆心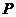 在(2)的抛物线上运动,
在(2)的抛物线上运动,
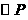 与两坐标轴都相切时,求
与两坐标轴都相切时,求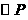 半径
半径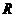 的值.
的值.
21、 (2008台湾) 如图,圆O1、圆O2、圆O3三圆两两相切,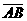 为圆O1、圆O2的公切线,
为圆O1、圆O2的公切线,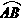 为半圆,且分别与三圆各切于一点。若圆O1、圆O2的半径均为1,则圆O3的半径为何?( )
为半圆,且分别与三圆各切于一点。若圆O1、圆O2的半径均为1,则圆O3的半径为何?( )
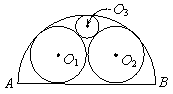

A. 1 B. 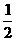 C.
C. 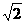 -1 D.
-1 D. 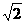 +1
+1
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com