
题目列表(包括答案和解析)
13.(08江苏淮安)(本题答案暂缺)28.(本小题14分)
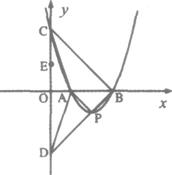
如图所示,在平面直角坐标系中.二次函数y=a(x-2)2-1图象的顶点为P,与x轴交点为 A、B,与y轴交点为C.连结BP并延长交y轴于点D.
(1)写出点P的坐标;
(2)连结AP,如果△APB为等腰直角三角形,求a的值及点C、D的坐标;
(3)在(2)的条件下,连结BC、AC、AD,点E(0,b)在线段CD(端点C、D除外)上,将△BCD绕点E逆时针方向旋转90°,得到一个新三角形.设该三角形与△ACD重叠部分的面积为S,根据不同情况,分别用含b的代数式表示S.选择其中一种情况给出解答过程,其它情况直接写出结果;判断当b为何值时,重叠部分的面积最大?写出最大值.
14.(08江苏常州)(本题答案暂缺)28.如图,抛物线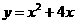 与x轴分别相交于点B、O,它的顶点为A,连接AB,把AB所的直线沿y轴向上平移,使它经过原点O,得到直线l,设P是直线l上一动点.
与x轴分别相交于点B、O,它的顶点为A,连接AB,把AB所的直线沿y轴向上平移,使它经过原点O,得到直线l,设P是直线l上一动点.
(1) 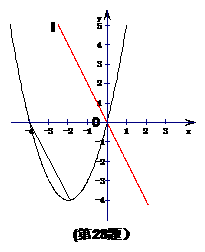 求点A的坐标;
求点A的坐标;
(2) 以点A、B、O、P为顶点的四边形中,有菱形、等腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P的坐标;
(3) 设以点A、B、O、P为顶点的四边形的面积为S,点P的横坐标为x,当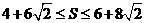 时,求x的取值范围.
时,求x的取值范围.
32.(08山东青岛)24.(本小题满分12分)
已知:如图①,在 中,
中,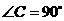 ,
,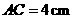 ,
,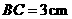 ,点
,点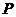 由
由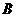 出发沿
出发沿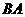 方向向点
方向向点 匀速运动,速度为1cm/s;点
匀速运动,速度为1cm/s;点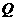 由
由 出发沿
出发沿 方向向点
方向向点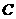 匀速运动,速度为2cm/s;连接
匀速运动,速度为2cm/s;连接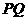 .若设运动的时间为
.若设运动的时间为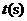 (
(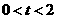 ),解答下列问题:
),解答下列问题:
(1)当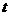 为何值时,
为何值时,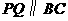 ?
?
(2)设 的面积为
的面积为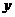 (
(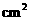 ),求
),求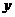 与
与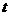 之间的函数关系式;
之间的函数关系式;
(3)是否存在某一时刻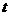 ,使线段
,使线段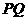 恰好把
恰好把 的周长和面积同时平分?若存在,求出此时
的周长和面积同时平分?若存在,求出此时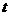 的值;若不存在,说明理由;
的值;若不存在,说明理由;
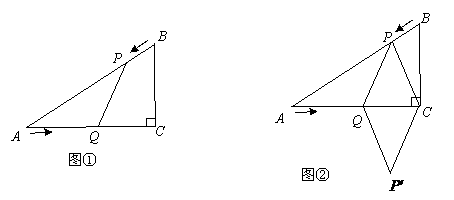 (4)如图②,连接
(4)如图②,连接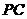 ,并把
,并把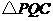 沿
沿 翻折,得到四边形
翻折,得到四边形 ,那么是否存在某一时刻
,那么是否存在某一时刻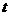 ,使四边形
,使四边形 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
(08山东青岛24题解析)24.(本小题满分12分)
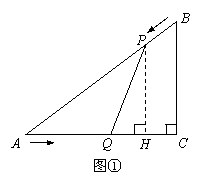 解:(1)在Rt△ABC中,
解:(1)在Rt△ABC中,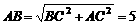 ,
,
由题意知:AP = 5-t,AQ = 2t,
若PQ∥BC,则△APQ ∽△ABC,
∴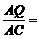
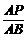 ,
,
∴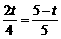 ,
,
∴ . ··································································································· 3′
. ··································································································· 3′
(2)过点P作PH⊥AC于H.
∵△APH ∽△ABC,
∴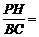
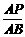 ,
,
∴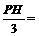
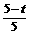 ,
,
∴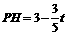 ,
,
∴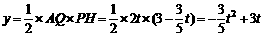 . ··········································· 6′
. ··········································· 6′
(3)若PQ把△ABC周长平分,
则AP+AQ=BP+BC+CQ.
∴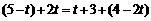 ,
,
解得: .
.
若PQ把△ABC面积平分,
则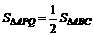 , 即-
, 即- +3t=3.
+3t=3.
∵ t=1代入上面方程不成立,
∴不存在这一时刻t,使线段PQ把Rt△ACB的周长和面积同时平分.················ 9′
(4)过点P作PM⊥AC于M,PN⊥BC于N,
若四边形PQP ′ C是菱形,那么PQ=PC.
∵PM⊥AC于M,
∴QM=CM.
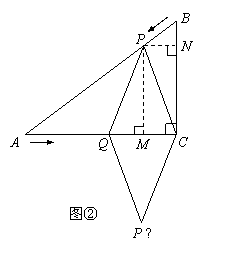 ∵PN⊥BC于N,易知△PBN∽△ABC.
∵PN⊥BC于N,易知△PBN∽△ABC.
∴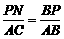 ,
∴
,
∴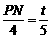 ,
,
∴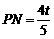 ,
,
∴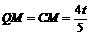 ,
,
∴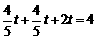 ,
,
解得: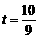 .
.
∴当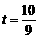 时,四边形PQP ′ C 是菱形.
时,四边形PQP ′ C 是菱形.
此时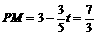 ,
, 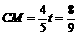 ,
,
在Rt△PMC中,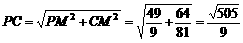 ,
,
∴菱形PQP ′ C边长为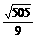 . 12′
. 12′
33(08山东泰安)26.(本小题满分10分)
在等边 中,点
中,点 为
为 上一点,连结
上一点,连结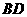 ,直线
,直线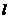 与
与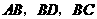 分别相交于点
分别相交于点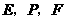 ,且
,且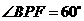 .
.
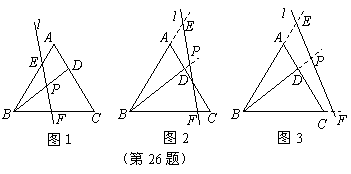

(1)如图1,写出图中所有与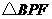 相似的三角形,并选择其中一对给予证明;
相似的三角形,并选择其中一对给予证明;
(2)若直线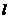 向右平移到图2、图3的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不证明),若不成立,请说明理由;
向右平移到图2、图3的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不证明),若不成立,请说明理由;
(3)探究:如图1,当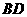 满足什么条件时(其它条件不变),
满足什么条件时(其它条件不变),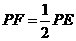 ?请写出探究结果,并说明理由.
?请写出探究结果,并说明理由.
(说明:结论中不得含有未标识的字母)
(08山东泰安26题解析)26.(本小题满分10分)
(1)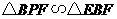 与
与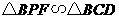 ······························································ 2分
······························································ 2分
以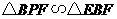 为例,证明如下:
为例,证明如下:
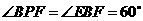
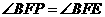
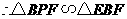 ····································································································· 4分
····································································································· 4分
(2)均成立,均为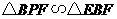 ,
,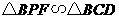 ········································· 6分
········································· 6分
(3)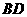 平分
平分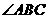 时,
时,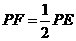 .····································································· 7分
.····································································· 7分
证明: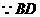 平分
平分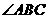
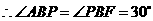
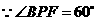
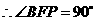
 ··············································································································· 8分
··············································································································· 8分
又
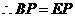
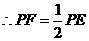 ············································································································· 10分
············································································································· 10分
注:所有其它解法均酌情赋分.
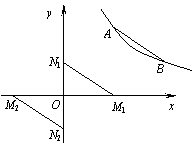
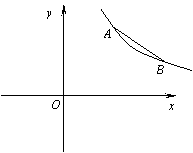 34(08山东威海)24.(11分) 如图,点A(m,m+1),B(m+3,m-1)都在反比例函数
34(08山东威海)24.(11分) 如图,点A(m,m+1),B(m+3,m-1)都在反比例函数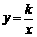 的图象上.
的图象上.
(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点,
以点A,B,M,N为顶点的四边形是平行四边形,
试求直线MN的函数表达式.
(3)选做题:在平面直角坐标系中,点P的坐标
为(5,0),点Q的坐标为(0,3),把线段PQ向右平
移4个单位,然后再向上平移2个单位,得到线段P1Q1,
则点P1的坐标为 ,点Q1的坐标为 .
(08山东威海24题解析)24.(本小题满分11分)
解:(1)由题意可知,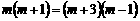 .
.
解,得 m=3. ………………………………3分
∴ A(3,4),B(6,2);
∴ k=4×3=12. ……………………………4分
(2)存在两种情况,如图:
①当M点在x轴的正半轴上,N点在y轴的正半轴
上时,设M1点坐标为(x1,0),N1点坐标为(0,y1).
∵ 四边形AN1M1B为平行四边形,
∴ 线段N1M1可看作由线段AB向左平移3个单位,
再向下平移2个单位得到的(也可看作向下平移2个单位,再向左平移3个单位得到的).
由(1)知A点坐标为(3,4),B点坐标为(6,2),
∴ N1点坐标为(0,4-2),即N1(0,2); ………………………………5分
M1点坐标为(6-3,0),即M1(3,0). ………………………………6分
设直线M1N1的函数表达式为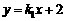 ,把x=3,y=0代入,解得
,把x=3,y=0代入,解得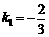 .
.
∴ 直线M1N1的函数表达式为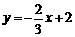 . ……………………………………8分
. ……………………………………8分
②当M点在x轴的负半轴上,N点在y轴的负半轴上时,设M2点坐标为(x2,0),N2点坐标为(0,y2).
∵ AB∥N1M1,AB∥M2N2,AB=N1M1,AB=M2N2,
∴ N1M1∥M2N2,N1M1=M2N2.
∴ 线段M2N2与线段N1M1关于原点O成中心对称.
∴ M2点坐标为(-3,0),N2点坐标为(0,-2). ………………………9分
设直线M2N2的函数表达式为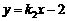 ,把x=-3,y=0代入,解得
,把x=-3,y=0代入,解得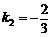 ,
,
∴ 直线M2N2的函数表达式为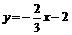 .
.
所以,直线MN的函数表达式为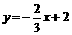 或
或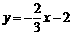 . ………………11分
. ………………11分
(3)选做题:(9,2),(4,5). ………………………………………………2分
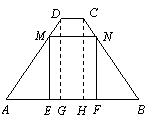
35(08山东威海)25.(12分) 如图,在梯形ABCD中,AB∥CD,AB=7,CD=1,AD=BC=5.点M,N分别在边AD,BC上运动,并保持MN∥AB,ME⊥AB,NF⊥AB,垂足分别为E,F.
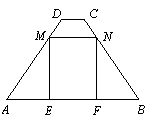 (1)求梯形ABCD的面积;
(1)求梯形ABCD的面积;
(2)求四边形MEFN面积的最大值.
(3)试判断四边形MEFN能否为正方形,若能,
求出正方形MEFN的面积;若不能,请说明理由.
(08山东威海25题解析)25.(本小题满分12分)
解:(1)分别过D,C两点作DG⊥AB于点G,CH⊥AB于点H. ……………1分
∵ AB∥CD,
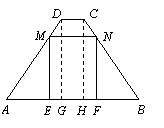 ∴ DG=CH,DG∥CH.
∴ DG=CH,DG∥CH.
∴ 四边形DGHC为矩形,GH=CD=1.
∵ DG=CH,AD=BC,∠AGD=∠BHC=90°,
∴ △AGD≌△BHC(HL).
∴ AG=BH=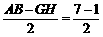 =3. ………2分
=3. ………2分
∵ 在Rt△AGD中,AG=3,AD=5,
∴ DG=4.
∴ 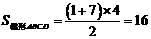 . ………………………………………………3分
. ………………………………………………3分
 (2)∵ MN∥AB,ME⊥AB,NF⊥AB,
(2)∵ MN∥AB,ME⊥AB,NF⊥AB,
∴ ME=NF,ME∥NF.
∴ 四边形MEFN为矩形.
∵ AB∥CD,AD=BC,
∴ ∠A=∠B.
∵ ME=NF,∠MEA=∠NFB=90°,
∴ △MEA≌△NFB(AAS).
∴ AE=BF. ……………………4分
设AE=x,则EF=7-2x. ……………5分
∵ ∠A=∠A,∠MEA=∠DGA=90°,
∴ △MEA∽△DGA.
∴ 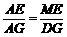 .
.
∴ ME=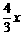 .
…………………………………………………………6分
.
…………………………………………………………6分
∴ 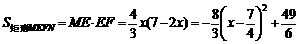 . ……………………8分
. ……………………8分
当x=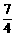 时,ME=
时,ME=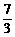 <4,∴四边形MEFN面积的最大值为
<4,∴四边形MEFN面积的最大值为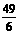 .……………9分
.……………9分
(3)能. ……………………………………………………………………10分
由(2)可知,设AE=x,则EF=7-2x,ME=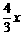 .
.
若四边形MEFN为正方形,则ME=EF.
即 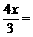 7-2x.解,得
7-2x.解,得 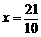 . ……………………………………………11分
. ……………………………………………11分
∴ EF=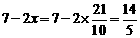 <4.
<4.
∴ 四边形MEFN能为正方形,其面积为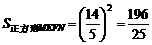 . ………12分
. ………12分
36(08山东潍坊)(本题答案暂缺)24.(本题满分12分)
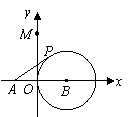 如图,圆
如图,圆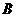 切
切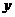 轴于原点
轴于原点 ,过定点
,过定点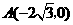 作圆
作圆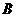 切线交圆于点
切线交圆于点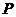 .已知
.已知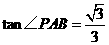 ,抛物线
,抛物线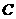 经过
经过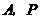 两点.
两点.
(1)求圆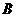 的半径;
的半径;
(2)若抛物线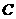 经过点
经过点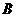 ,求其解析式;
,求其解析式;
(3)投抛物线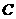 交
交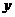 轴于点
轴于点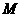 ,若三角形
,若三角形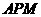 为直角三角形,求点
为直角三角形,求点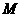 的坐标.
的坐标.
37(08山东烟台)25、(本题满分14分)
如图,抛物线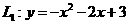 交
交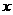 轴于A、B两点,交
轴于A、B两点,交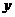 轴于M点.抛物线
轴于M点.抛物线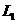 向右平移2个单位后得到抛物线
向右平移2个单位后得到抛物线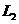 ,
,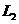 交
交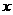 轴于C、D两点.
轴于C、D两点.
(1)求抛物线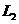 对应的函数表达式;
对应的函数表达式;
(2)抛物线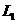 或
或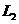 在
在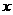 轴上方的部分是否存在点N,使以A,C,M,N为顶点的四边形是平行四边形.若存在,求出点N的坐标;若不存在,请说明理由;
轴上方的部分是否存在点N,使以A,C,M,N为顶点的四边形是平行四边形.若存在,求出点N的坐标;若不存在,请说明理由;
(3)若点P是抛物线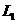 上的一个动点(P不与点A、B重合),那么点P关于原点的对称点Q是否在抛物线
上的一个动点(P不与点A、B重合),那么点P关于原点的对称点Q是否在抛物线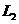 上,请说明理由.
上,请说明理由.




38(08山东枣庄)25.(本题满分10分)
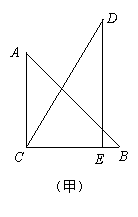
把一副三角板如图甲放置,其中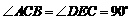 ,
,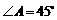 ,
,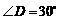 ,斜边
,斜边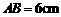 ,
,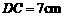 .把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点
.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点 ,与D1E1相交于点F.
,与D1E1相交于点F.
(1)求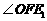 的度数;
的度数;
(2)求线段AD1的长;
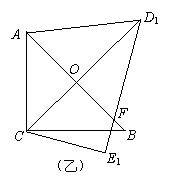
 (3)若把三角形D1CE1绕着点
(3)若把三角形D1CE1绕着点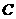 顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由.
顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由.
 (08山东枣庄25题解析)25.(本题满分10分)
(08山东枣庄25题解析)25.(本题满分10分)
解:(1)如图所示,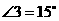 ,
,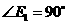 ,
,
∴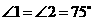 . ………………………………1分
. ………………………………1分
又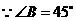 ,
,
∴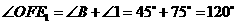 . ………3分
. ………3分
(2)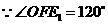 ,∴∠D1FO=60°.
,∴∠D1FO=60°.
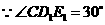 ,∴
,∴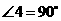 . ··································································· 4分
. ··································································· 4分
又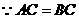 ,
,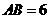 ,∴
,∴ .
.
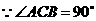 ,∴
,∴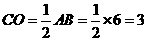 .····················································· 5分
.····················································· 5分
又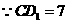 ,∴
,∴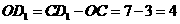 .
.
在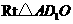 中,
中,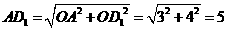 .································· 6分
.································· 6分
(3)点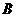 在
在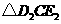 内部. ··········································································· 7分
内部. ··········································································· 7分
理由如下:设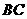 (或延长线)交
(或延长线)交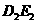 于点P,则
于点P,则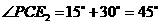 .
.
在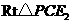 中,
中,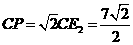 , …………·································· 9分
, …………·································· 9分
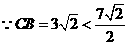 ,即
,即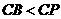 ,∴点
,∴点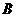 在
在 内部. ……………10分
内部. ……………10分
30.(08山东临沂)25.(本小题满分11分)
已知∠MAN,AC平分∠MAN。
⑴在图1中,若∠MAN=120°,∠ABC=∠ADC=90°,求证:AB+AD=AC;
⑵在图2中,若∠MAN=120°,∠ABC+∠ADC=180°,则⑴中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
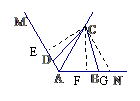
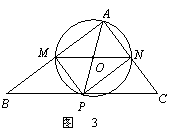
⑶在图3中:
①若∠MAN=60°,∠ABC+∠ADC=180°,则AB+AD=____AC;
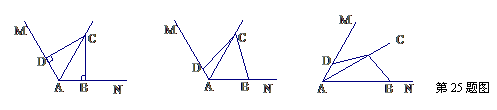 ②若∠MAN=α(0°<α<180°),∠ABC+∠ADC=180°,则AB+AD=____AC(用含α的三角函数表示),并给出证明。
②若∠MAN=α(0°<α<180°),∠ABC+∠ADC=180°,则AB+AD=____AC(用含α的三角函数表示),并给出证明。
(08山东临沂25题解析)25.解:⑴证明:∵AC平分∠MAN,∠MAN=120°,
∴∠CAB=∠CAD=60°,
 ∵∠ABC=∠ADC=90°,
∵∠ABC=∠ADC=90°,
∴∠ACB=∠ACD=30°,…………1分
∴AB=AD=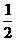 AC,……………………2分
AC,……………………2分
∴AB+AD=AC。……………………3分
⑵成立。……………………………r…4分
证法一:如图,过点C分别作AM、AN的垂线,垂足分别为E、F。
∵AC平分∠MAN,∴CE=CF.
∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,
∴∠CDE=∠ABC,………………………………………………………………5分
∵∠CED=∠CFB=90°,∴△CED≌△CFB,∴ED=FB,……………………6分
∴AB+AD=AF+BF+AE-ED=AF+AE,由⑴知AF+AE=AC,
∴AB+AD=AC……………………………………………………………………7分
证法二:如图,在AN上截取AG=AC,连接CG.
∵∠CAB=60°,AG=AC,∴∠AGC=60°,CG=AC=AG,…………5分
∵∠ABC+∠ADC=180°,∠ABC+∠CBG=180°,
∴∠CBG=∠ADC,∴△CBG≌△CDA,……………………………………6分
∴BG=AD,
∴AB+AD=AB+BG=AG=AC,…………………………………………7分
⑶①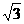 ;………………………………………………………………………8分
;………………………………………………………………………8分
②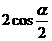 .………………………………………………………………………9分
.………………………………………………………………………9分
证明:由⑵知,ED=BF,AE=AF,
在Rt△AFC中,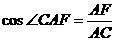 ,即
,即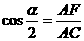 ,
,
∴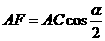 ,………………………………………………………………10分
,………………………………………………………………10分
∴AB+AD=AF+BF+AE-ED=AF+AE=2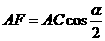 ,…………11分
,…………11分
31(08山东临沂)26.(本小题满分13分)
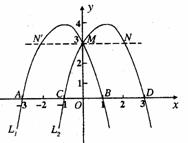
如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3)。
⑴求抛物线的解析式;
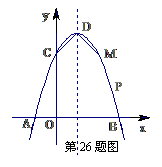 ⑵设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
⑵设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
⑶若点M是抛物线上一点,以B、C、D、M为顶点的四边形是直角梯形,试求出点M的坐标。
(08山东临沂26题解析)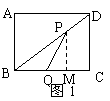 26.⑴∵抛物线与y轴交于点C(0,3),
26.⑴∵抛物线与y轴交于点C(0,3),
∴设抛物线解析式为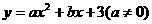 ………1分
………1分
根据题意,得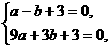 ,解得
,解得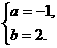
∴抛物线的解析式为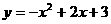 ………………………………………2分
………………………………………2分
⑵存在。…………………………………………………………………………3分
由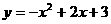 得,D点坐标为(1,4),对称轴为x=1。…………4分
得,D点坐标为(1,4),对称轴为x=1。…………4分
①若以CD为底边,则PD=PC,设P点坐标为(x,y),根据勾股定理,
得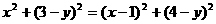 ,即y=4-x。…………………………5分
,即y=4-x。…………………………5分
又P点(x,y)在抛物线上,∴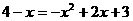 ,即
,即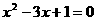 …………6分
…………6分
解得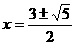 ,
,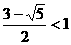 ,应舍去。∴
,应舍去。∴ 。……………………7分
。……………………7分
∴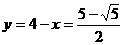 ,即点P坐标为
,即点P坐标为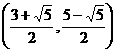 。……………………8分
。……………………8分
②若以CD为一腰,因为点P在对称轴右侧的抛物线上,由抛物线对称性知,点P与点C关于直线x=1对称,此时点P坐标为(2,3)。
∴符合条件的点P坐标为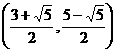 或(2,3)。……………………9分
或(2,3)。……………………9分
⑶由B(3,0),C(0,3),D(1,4),根据勾股定理,
得CB=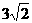 ,CD=
,CD=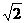 ,BD=
,BD=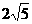 ,………………………………………………10分
,………………………………………………10分
∴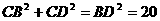 ,
,
∴∠BCD=90°,………………………………………………………………………11分
设对称轴交x轴于点E,过C作CM⊥DE,交抛物线于点M,垂足为F,在Rt△DCF中,
∵CF=DF=1,
∴∠CDF=45°,
由抛物线对称性可知,∠CDM=2×45°=90°,点坐标M为(2,3),
∴DM∥BC,
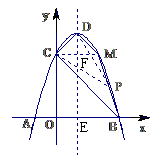 ∴四边形BCDM为直角梯形, ………………12分
∴四边形BCDM为直角梯形, ………………12分
由∠BCD=90°及题意可知,
以BC为一底时,顶点M在抛物线上的直角梯形只有上述一种情况;
以CD为一底或以BD为一底,且顶点M在抛物线上的直角梯形均不存在。
综上所述,符合条件的点M的坐标为(2,3)。……………13分
29.(08山东德州东营菏泽)24.(本题满分12分)
在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
 (3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?

(08山东德州东营菏泽23题解析)23.(本题满分12分)
解:(1)∵MN∥BC,∴∠AMN=∠B,∠ANM=∠C.
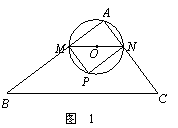 ∴ △AMN ∽ △ABC.
∴ △AMN ∽ △ABC.
∴ 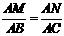 ,即
,即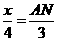 .
.
∴ AN=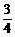 x. ……………2分
x. ……………2分
∴ 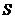 =
=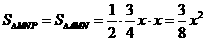 .(0<
.(0<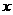 <4) ………………3分
<4) ………………3分
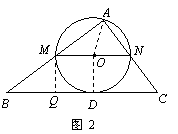 (2)如图2,设直线BC与⊙O相切于点D,连结AO,OD,则AO =OD =
(2)如图2,设直线BC与⊙O相切于点D,连结AO,OD,则AO =OD =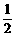 MN.
MN.
在Rt△ABC中,BC =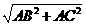 =5.
=5.
由(1)知 △AMN ∽ △ABC.
∴ 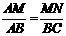 ,即
,即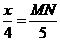 .
.
∴ 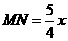 ,
,
∴ 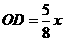 . …………………5分
. …………………5分
过M点作MQ⊥BC
于Q,则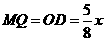 .
.
在Rt△BMQ与Rt△BCA中,∠B是公共角,
∴ △BMQ∽△BCA.
∴ 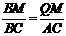 .
.
∴ 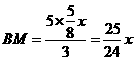 ,
,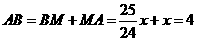 .
.
∴ x=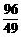 .
.
∴ 当x=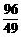 时,⊙O与直线BC相切.…………………………………………7分
时,⊙O与直线BC相切.…………………………………………7分
 (3)随点M的运动,当P点落在直线BC上时,连结AP,则O点为AP的中点.
(3)随点M的运动,当P点落在直线BC上时,连结AP,则O点为AP的中点.
∵ MN∥BC,∴ ∠AMN=∠B,∠AOM=∠APC.
∴ △AMO ∽ △ABP.
∴ 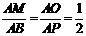 . AM=MB=2.
. AM=MB=2.
故以下分两种情况讨论:
① 当0<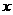 ≤2时,
≤2时,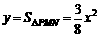 .
.
∴ 当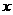 =2时,
=2时,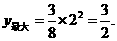 …………………………………………8分
…………………………………………8分
② 当2<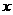 <4时,设PM,PN分别交BC于E,F.
<4时,设PM,PN分别交BC于E,F.
 ∵ 四边形AMPN是矩形,
∵ 四边形AMPN是矩形,
∴ PN∥AM,PN=AM=x.
又∵ MN∥BC,
∴ 四边形MBFN是平行四边形.
∴ FN=BM=4-x.
∴ 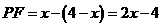 .
.
又△PEF ∽ △ACB.
∴ 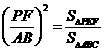 .
.
∴ 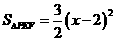 . ……………………………………………………… 9分
. ……………………………………………………… 9分
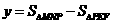 =
=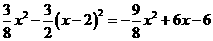 .……………………10分
.……………………10分
当2<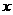 <4时,
<4时,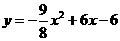
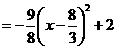 .
.
∴ 当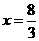 时,满足2<
时,满足2<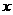 <4,
<4,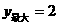 . ……………………………11分
. ……………………………11分
综上所述,当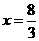 时,
时,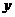 值最大,最大值是2. ……………………………12分
值最大,最大值是2. ……………………………12分
28.(08山东滨州)24.(本题满分12分)
如图(1),已知在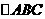 中,AB=AC=10,AD为底边BC上的高,且AD=6。将
中,AB=AC=10,AD为底边BC上的高,且AD=6。将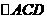 沿箭头所示的方向平移,得到
沿箭头所示的方向平移,得到 。如图(2),
。如图(2), 交AB于E,
交AB于E, 分别交AB、AD于G、F。以
分别交AB、AD于G、F。以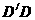 为直径作
为直径作 ,设
,设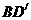 的长为x,
的长为x, 的面积为y。
的面积为y。
(1)求y与x之间的函数关系式及自变量x的取值范围;
(2)连结EF,求EF与 相切时x的值;
相切时x的值;
(3)设四边形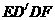 的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?
的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?

(08山东滨州24题解析)24.
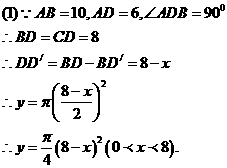


27.(08山东滨州)23、(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
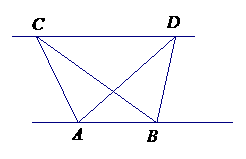
(2)结论应用:①如图2,点M、N在反比例函数y=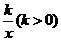 的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试应用(1)中得到的结论证明:MN∥EF.
的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试应用(1)中得到的结论证明:MN∥EF.
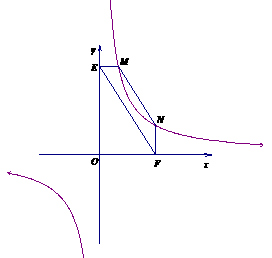
②若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断MN与E是否平行.
(08山东滨州23题解析)23.(1)证明:分别过点C、D作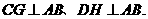
垂足为G、H,则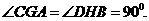

(2)①证明:连结MF,NE
设点M的坐标为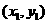 ,点N的坐标为
,点N的坐标为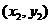 ,
,
∵点M,N在反比例函数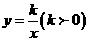 的图象上,
的图象上,
∴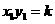 ,
,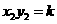
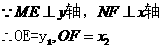
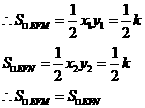
由(1)中的结论可知:MN∥EF。
②MN∥EF。

3.第(4)问图形画得大致正确的得2分,只画出图形一部分的得1分.
2.第(3)问表格数据,每填对其中4空得1分;
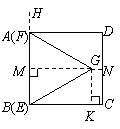
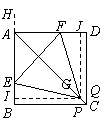
26.(08江西南昌)25.如图1,正方形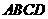 和正三角形
和正三角形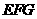 的边长都为1,点
的边长都为1,点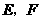 分别在线段
分别在线段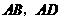 上滑动,设点
上滑动,设点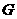 到
到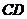 的距离为
的距离为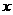 ,到
,到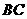 的距离为
的距离为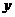 ,记
,记 为
为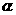 (当点
(当点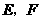 分别与
分别与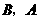 重合时,记
重合时,记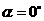 ).
).
(1)当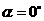 时(如图2所示),求
时(如图2所示),求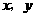 的值(结果保留根号);
的值(结果保留根号);
(2)当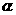 为何值时,点
为何值时,点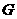 落在对角形
落在对角形 上?请说出你的理由,并求出此时
上?请说出你的理由,并求出此时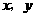 的值(结果保留根号);
的值(结果保留根号);
(3)请你补充完成下表(精确到0.01):
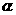 |
 |
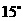 |
 |
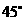 |
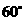 |
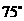 |
 |
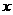 |
|
0.03 |
0 |
|
|
0.29 |
|
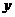 |
|
0.29 |
0.13 |
|
|
0.03 |
|
(4)若将“点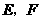 分别在线段
分别在线段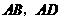 上滑动”改为“点
上滑动”改为“点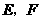 分别在正方形
分别在正方形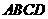 边上滑动”.当滑动一周时,请使用(3)的结果,在图4中描出部分点后,勾画出点
边上滑动”.当滑动一周时,请使用(3)的结果,在图4中描出部分点后,勾画出点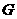 运动所形成的大致图形.
运动所形成的大致图形.
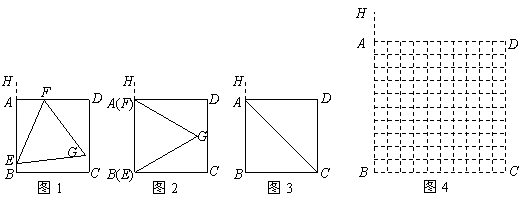 (参考数据:
(参考数据: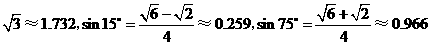 .)
.)
(08江西南昌25题解析)25.解:(1)过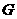 作
作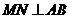 于
于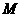 交
交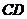 于
于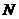 ,
,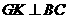 于
于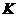 .
.
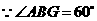 ,
,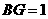 ,
,
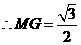 ,
,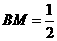 .······················································································ 2分
.······················································································ 2分
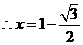 ,
,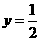 .························································································· 3分
.························································································· 3分
 (2)当
(2)当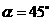 时,点
时,点 在对角线
在对角线 上,其理由是:·········································· 4分
上,其理由是:·········································· 4分
过 作
作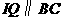 交
交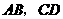 于
于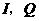 ,
,
过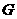 作
作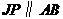 交
交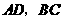 于
于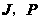 .
.
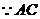 平分
平分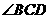 ,
,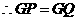 ,
,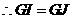 .
.
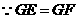 ,
,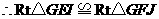 ,
,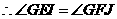 .
.
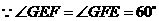 ,
,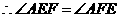 .
.
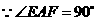 ,
,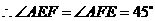 .
.
 即
即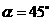 时,点
时,点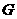 落在对角线
落在对角线 上.································································ 6分
上.································································ 6分
(以下给出两种求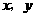 的解法)
的解法)
方法一: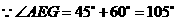 ,
, .
.
在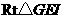 中,
中,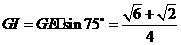 ,
,
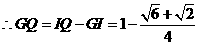 .·········································································· 7分
.·········································································· 7分
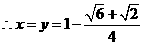 .························································································ 8分
.························································································ 8分
方法二:当点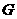 在对角线
在对角线 上时,有
上时,有
 ,··························································································· 7分
,··························································································· 7分
解得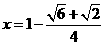
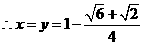 .························································································ 8分
.························································································ 8分
(3)
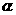 |
 |
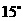 |
 |
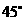 |
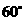 |
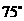 |
 |
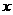 |
0.13 |
0.03 |
0 |
0.03 |
0.13 |
0.29 |
0.50 |
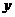 |
0.50 |
0.29 |
0.13 |
0.03 |
0 |
0.03 |
0.13 |
································································ 10分
(4)由点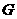 所得到的大致图形如图所示:
所得到的大致图形如图所示:

 ··························································································· 12分
··························································································· 12分
说明:1.第(2)问回答正确的得1分,证明正确的得2分,求出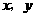 的值各得1分;
的值各得1分;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com