
题目列表(包括答案和解析)
5.小明用一个半径为5 ,面积为15
,面积为15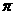
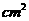 的扇形纸片,制作成一个圆锥的侧面(接缝处不重叠),那么这个圆锥的底面半径为( )
的扇形纸片,制作成一个圆锥的侧面(接缝处不重叠),那么这个圆锥的底面半径为( )
A.3 B.4
B.4 C.5
C.5 D.15
D.15
4. 在一个晴朗的上午,小明拿着一块正方形木板在阳光下做投影实验,则该正方形木块在地面上形成的投影不可能是( )
在一个晴朗的上午,小明拿着一块正方形木板在阳光下做投影实验,则该正方形木块在地面上形成的投影不可能是( )
3.已知二次函数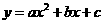 中,其函数
中,其函数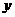 与自变量
与自变量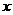 之间的部分对应值如下表所示:
之间的部分对应值如下表所示:
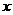 |
… |
0 |
1 |
2 |
3 |
… |
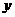 |
… |
5 |
2 |
1 |
2 |
… |
点A(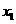 ,
,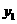 )、B(
)、B(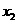 ,
,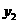 )在函数的图象上,则当
)在函数的图象上,则当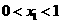 ,
,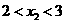 时,
时,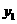 与
与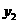 的大小关系正确的是( )
的大小关系正确的是( )
A.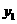 ≥
≥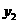 B.
B.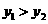 C.
C.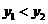 D.
D.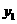 ≤
≤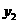
2.某种禽流感病毒变异后的直径为0.00000012米,将这个数写成科学记数法是( )
A. 1.2×10-5 B. 0.12×10-6 C. 1.2×10-7 D. 12×10-8
1. 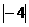 的算术平方根是( )
的算术平方根是( )
A. 4 B. -4 C. 2 D. ±2
25.(12分)一条抛物线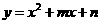 经过点
经过点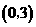 与
与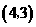 .
.
(1)求这条抛物线的解析式,并写出它的顶点坐标;
(2)现有一半径为1、圆心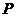 在抛物线上运动的动圆,当
在抛物线上运动的动圆,当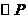 与坐标轴相切时,求圆心
与坐标轴相切时,求圆心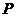 的坐标;
的坐标;
(3)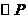 能与两坐标轴都相切吗?如果不能,试通过上下平移抛物线
能与两坐标轴都相切吗?如果不能,试通过上下平移抛物线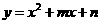 使
使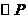 与两坐标轴都相切(要说明平移方法).
与两坐标轴都相切(要说明平移方法).
24.(7分)在保护地球爱护家园活动中,校团委把一批树苗分给初三(1)班同学去栽种.如果每人分2棵,还剩42棵;如果前面每人分3棵,那么最后一人得到的树苗少于5棵(但至少分得一棵).
(1)设初三(1)班有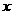 名同学,则这批树苗有多少棵?(用含
名同学,则这批树苗有多少棵?(用含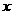 的代数式表示).
的代数式表示).
23.(6分)如图,某学习小组为了测量河对岸塔AB的高度,在塔底部B的正对岸点C处,测得仰角∠ACB=30°.
(1)若河宽BC是60米,求塔AB的高(结果精确到0.1米);(4分) 参考数据: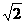 ≈1.414,
≈1.414,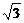 ≈1.732)
( 2)若河宽BC的长度无法度量,如何测量塔AB的高度呢?小明想出了另外一种方法:从点C出发,
≈1.732)
( 2)若河宽BC的长度无法度量,如何测量塔AB的高度呢?小明想出了另外一种方法:从点C出发,
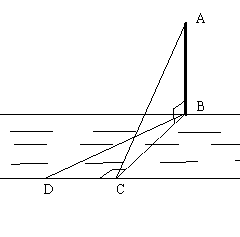 沿河岸CD的方向(点B、C、D在同一平面内,且CD⊥BC)走
沿河岸CD的方向(点B、C、D在同一平面内,且CD⊥BC)走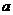 米,到达D处,测得∠BDC=60°,这样就可以求得塔AB的高度了.请你用这种方法求出塔AB的高.
米,到达D处,测得∠BDC=60°,这样就可以求得塔AB的高度了.请你用这种方法求出塔AB的高.
解:
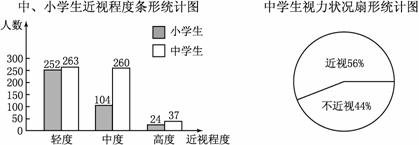
22.(7分).某市青少年健康研究中心随机抽取了本市1000名小学生和若干名中学生,对他们的视力状况进行了调查,并把调查结果绘制成如下统计图(近视程度分为轻度、中度、高度三种).
(1)求这1000名小学生患近视的百分比;
(2)求本次抽查的中学生人数;
(3)该市有中学生8万人,小学生10万人,分别估计该市的中 学生与小学生患“中度近视”的人数.
学生与小学生患“中度近视”的人数.
21.(6分)某商场家电销售部有营业员20名,为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售额目标,根据目标完成情况对营业员进行适当的奖惩.为此,商场统计了这20名营业员在某月的销售额,数据如下:(单位:万元)
25 26 21 17 28 26 20 25 26 30
20 21 20 26 30 25 21 19 28 26
(1)请根据以上信息完成下表:
|
销售额(万元) |
17 |
19 |
20 |
21 |
25 |
26 |
28 |
30 |
|
频数(人数) |
1 |
1 |
3 |
3 |
|
|
|
|
(2)上述数据中,众数是 万元,中位数是 万元,平均数是 万元;
(3)如果将众数作为月销售额目标,能否让至少一半的营业员都能达到目标?请说明理由
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com