2．(2009·广东文，4)若函数y＝f(x)是函数y＝a^x(a>0，且a≠1)的反函数，且f(2)＝1，则f(x)

＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．2^x－2

C．logx 　　　　　　　　　　　　　　　　　　　　　　 D．log₂x

解析　函数y＝a^x(a>0，且a≠1)的反函数是f(x)＝log_ax，又f(2)＝1，即log_a2＝1，所以a

＝2，故f(x)＝log₂x，故选D.

答案　D

1．(2009·湖南文，1)log₂的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．－　 　　　　　　　　　　　 B.　 　　　　　　　　 C．－ 　　　　　　　 　D.

解析　log₂＝log₂2＝.

答案　D

12．(14分)(2009·宁波模拟)已知函数f(x)＝ 满足f(c²)＝.

(1)求常数c的值；

(2)解不等式f(x)>+1.

解　(1)依题意0<c<1，∴c²<c，

∵f(c²)＝，∴c³+1＝，c＝.

(2)由(1)得f(x)＝，

由f(x)>+1得

当0<x<时，x+1>+1，∴<x<，

当≤x<1时，2^－4x+1>+1，∴≤x<.

综上可知：<x<，

∴f(x)>+1的解集为.

§2.5　对数与对数函数

11．(13分)(2009·中山一模)若函数y＝a^2x+2a^x－1(a>0且a≠1)在x∈[－1,1]上的最大值为14，

求a的值．

解　令a^x＝t，∴t>0，则y＝t²+2t－1＝(t+1)²－2，其对称轴为t＝－1.该二次函数在[－1，

+∞)上是增函数．

①若a>1，∵x∈[－1,1]，∴t＝a^x∈，

故当t＝a，即x＝1时，y_max＝a²+2a－1＝14，

解得a＝3(a＝－5舍去)．

②若0<a<1，∵x∈[－1,1]，

∴t＝a^x∈，故当t＝，即x＝－1时，

y _max＝²－2＝14.∴a＝或－(舍去)．

综上可得a＝3或.

10．(13分)(2010·临沂月考)已知对任意x∈R，不等式>2x²－mx+m+4恒成立，求

实数m的取值范围．

解　由题知：不等式x²+x>2x²－mx+m+4对x∈R恒成立，∴x²+x<2x²－mx+m+4对x∈R恒成立．

∴x²－(m+1)x+m+4>0对x∈R恒成立．

∴Δ＝(m+1)²－4(m+4)<0.

∴m²－2m－15<0.∴－3<m<5.

9．(2009·江苏)已知a＝，函数f(x)＝a^x，若实数m、n满足f(m)>f(n)，则m、n的大小

关系为________．

解析　∵0<a＝<1，∴函数f(x)＝a^x在R上是减函数．又∵f(m)>f(n)，∴m<n.

答案　m<n

8．(2010·济宁调研)设函数f(x)＝a^－|x| (a>0且a≠1)，若f(2)＝4，则f(－2)与f(1)的大小关系是__________．

解析　由f(2)＝a^－2＝4，解得a＝，

∴f(x)＝2^|x|，∴f(－2)＝4>2＝f(1)．

答案　f(－2)>f(1)

7．(2009·青岛一模)若f(x)＝a^－x与g(x)＝a^x－a (a>0且a≠1)的图象关于直线x＝1对称，则a＝________.

解析　g(x)上的点P(a,1)关于直线x＝1的对称点P′(2－a,1)应在f(x)＝a^－x上，

∴1＝a^a－2.∴a－2＝0，即a＝2.

答案　2

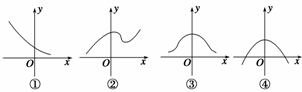
6．(2010·湖州联考)函数y＝·(2a－3)－的部分图象大致是如图所示的四个图象的一个，根据你的判断，a可能的取值是 　　　　　　　　　　　　　　　　　　　　　　　　　 (　 　)

A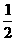．　 　　　　　　　　　　　　 B.　 　　　　　　　　　　 C．2　 　　　　　　　　 D．4

解析　函数为偶函数，排除①②，又函数值恒为正值，则排除④，故图象只能是③，再根

据图象先增后减的特征可知2a－3>1，即a>2，符合条件的只有D选项，故选D.

答案　D

5．(2009·珠海模拟)若函数f(x)＝，则该函数在(－∞，+∞)上是　　　　　　　　　　 (　)

A．单调递减无最小值　 　　　　　　　　　　　 B．单调递减有最小值

C．单调递增无最大值　 　　　　　　　　　　　 D．单调递增有最大值

解析　令u(x)＝2^x+1，则f(u)＝.因为u(x)在(－∞，+∞)上单调递增且u(x)>1，而f(u)＝在(1，+∞)上单调递减，故f(x)＝在(－∞，+∞)上单调递减，且无限趋于0，故无最小值．

答案　A