6．(2009·丽水模拟)已知函数f(x)是定义在R上的奇函数，当x>0时，f(x)＝1－2^－x，则不等式f(x)<－的解集是　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．(－∞，－1)　 　　　　　　　　　　　　　　　　　　　 B．(－∞，－1]

C．(1，+∞)　 　　　　　　　　　　　　　　　　　　　　　 D．[1，+∞)

解析　当x>0时，1－2^－x＝1－>0与题意不符，

当x<0时，－x>0，∴f(－x)＝1－2^x，

又∵f(x)为R上的奇函数，

∴f(－x)＝－f(x)，

∴－f(x)＝1－2^x，

∴f(x)＝2^x－1，

∴f(x)＝2^x－1<－，∴2^x<，∴x<－1，

∴不等式f(x)<－的解集是(－∞，－1)．

答案　A

5．(2009·湖南示范性高中一模)函数y＝f(x)与y＝g(x)有相同的定义域，且都不是常数函数，

对定义域中任意x，有f(x)+f(－x)＝0，g(x)g(－x)＝1，且x≠0，g(x)≠1，则F(x)＝

+f(x)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．是奇函数但不是偶函数

B．是偶函数但不是奇函数

C．既是奇函数又是偶函数

D．既不是奇函数也不是偶函数

解析　由条件知f(－x)＝－f(x)，g(－x)＝，

∴F(－x)＝+f(－x)＝－f(x)

＝＝＝F(x)．

答案　B

4．(2009·陕西文，10)定义在R上的偶函数f(x)，对任意x₁，x₂∈[0，+∞)(x₁≠x₂)，有

<0，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．f(3)<f(－2)<f(1)

B．f(1)<f(－2)<f(3)

C．f(－2)<f(1)<f(3)

D．f(3)<f(1)<f(－2)

解析　对任意x₁，x₂∈[0，+∞)(x₁≠x₂)，有<0，则x₂－x₁与f(x₂)－f(x₁)异号，因此函数f(x)在[0，+∞)上是减函数．又f(x)在R上是偶函数，故f(－2)＝f(2)，由于3>2>1，

故有f(3)<f(－2)<f(1)．

答案　A

3．(2009·辽宁理，9)已知偶函数f(x)在区间[0，+∞)上单调递增，则满足f(2x－1)<f()的x的取值范围是　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析　方法一　当2x－1≥0，即x≥时，因为f(x)在[0，+∞)上单调递增，故需满足2x

－1<，即x<，

所以≤x<.

当2x－1<0，即x<时，由于f(x)是偶函数，故f(x)在(－∞，0]上单调递减，f＝f，

此时需满足2x－1>－，所以<x<，综上可得<x<.

方法二　∵f(x)为偶函数，∴f(2x－1)＝f(|2x－1|)，

又∵f(x)在区间(0，+∞)上为增函数，

∴不等式f(2x－1)<f()等价于|2x－1|<.

∴－<2x－1<，

∴<x<.

答案　A

2．(2009·金华模拟)若函数f(x)是定义在R上的偶函数，在(－∞，0]上是减函数，且f(2)＝0，

则使得f(x)<0的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．(－∞，2)

B．(2，+∞)

C．(－∞，－2)∪(2，+∞)

D．(－2,2)

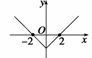解析　∵f(x)是偶函数且在(-∞，0]上是减函数，且f(2)=f(-2)=0，

可画示意图如图所示，由图知f(x)<0的解集为(-2,2)．

答案　D

1．(2010·吉林模拟)已知f(x)＝ax²+bx是定义在[a－1,2a]上的偶函数，那么a+b的值是(　)

A．－　 　　　　　　　　　　　 B. 　　　　　　　　　　 　　　 C.　 　　　　　　　　　　 D．－

解析　依题意得，∴，

∴a+b＝+0＝.

答案　B

12．(14分)(2009·宣城一模)f(x)是定义在(0，+∞)上的增函数，且f＝f(x)－f(y)．

(1)求f(1)的值；

(2)若f(6)＝1，解不等式f(x+3)－f<2.

解　(1)令x＝y，得f(1)＝0.

(2)由x+3>0及>0，得x>0,

由f(6)＝1及f(x+3)－f<2，

得f[x(x+3)]<2f(6)，

即f[x(x+3)]－f(6)<f(6)，

亦即f<f(6)．

因为f(x)在(0，+∞)上是增函数，

所以<6，

解得<x<.

综上所述，不等式的解集是.

§2.3　函数的奇偶性

11．(13分)(2010·青岛调研)已知f(x)＝ (x≠a)．

(1)若a＝－2，试证f(x)在(－∞，－2)内单调递增；

(2)若a>0且f(x)在(1，+∞)内单调递减，求a的取值范围．

(1)证明　任设x₁<x₂<－2，

则f(x₁)－f(x₂)＝－＝.

∵(x₁+2)(x₂+2)>0，x₁－x₂<0，

∴f(x₁)<f(x₂)，

∴f(x)在(－∞，－2)内单调递增．

(2)解　任设1<x₁<x₂，则

f(x₁)－f(x₂)＝－＝.

∵a>0，x₂－x₁>0，

∴要使f(x₁)－f(x₂)>0，只需(x₁－a)(x₂－a)>0恒成立，∴a≤1.

综上所述知0<a≤1.

10．(13分)(2010·芜湖一模)判断f(x)＝在(－∞，0)∪(0，+∞)上的单调性．

解　∵－1<1，f(－1)＝－1<f(1)＝1，

∴f(x)在(－∞，0)∪(0，+∞)上不是减函数．

∵－2<－1，f(－2)＝－>f(－1)＝－1，

∴f(x)在(－∞，0)∪(0，+∞)上不是增函数．

∴f(x)在(－∞，0)∪(0，+∞)上不具有单调性．

9．(2009·山东实验中学第一次诊断)已知定义域为D的函数f(x)，对任意x∈D，存在正数K，

都有|f(x)|≤K成立，则称函数f(x)是D上的“有界函数”．已知下列函数：①f(x)＝2sin x；

②f(x)＝；③f(x)＝1－2^x；④f(x)＝，其中是“有界函数”的是________．(写出所有满足要求的函数的序号)

解析　①中|f(x)|＝|2sin x|≤2，②中|f(x)|≤1；

④|f(x)|＝＝≤(x≠0)，

当x＝0时，f(x)＝0，总之，|f(x)|≤；

③f(x)<1,∴|f(x)|→+∞,故填①②④.

答案　①②④