
题目列表(包括答案和解析)
3.(1)含n个元素的集合的子集数为2n,真子集数为2n-1;非空真子集的数为2n-2;
(2)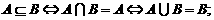 注意:讨论的时候不要遗忘了
注意:讨论的时候不要遗忘了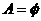 的情况。
的情况。
2.数形结合是解集合问题的常用方法:解题时要尽可能地借助数轴、直角坐标系或韦恩图等工具,将抽象的代数问题具体化、形象化、直观化,然后利用数形结合的思想方法解决;
1.理解集合中元素的意义是解决集合问题的关键:元素是函数关系中自变量的取值?还是因变量的取值?还是曲线上的点?… ;
18.(14分)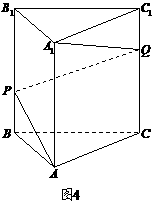 如图4,正三棱柱
如图4,正三棱柱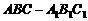 中,
中,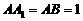 ,
,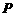 、
、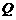 分别是侧棱
分别是侧棱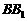 、
、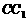 上的三等分点,
上的三等分点,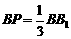 ,
,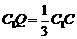 .
.
(1)证明:平面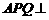 平面
平面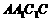 ;(2)求四面体
;(2)求四面体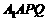 的体积.
的体积.
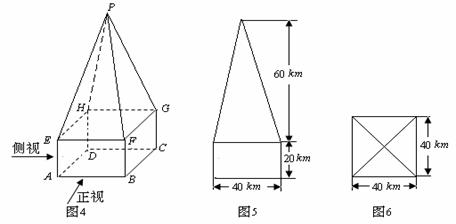
16.(14分)某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图.
(1)请画出该安全标识墩的侧(左)视图;(2)求该安全标识墩的体积(3)证明:直线BD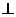 平面PEG
平面PEG
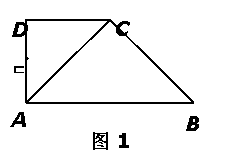
17(14分).如图1,在直角梯形ABCD中,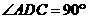 ,
,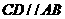 ,
,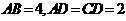 .将
.将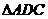 沿
沿 折起,使平面
折起,使平面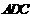
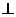 平面
平面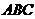 ,得到几何体
,得到几何体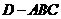 ,如图2所示.
,如图2所示.
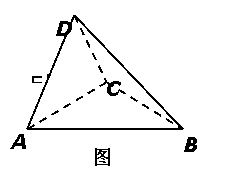
(Ⅰ)若E为AD的中点,试在线段CD上找一点F,使 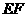 ∥平面ABC,并加以证明;
∥平面ABC,并加以证明;
 (Ⅱ)求证:
BC⊥平面
(Ⅱ)求证:
BC⊥平面 ;(Ⅲ)求几何体
;(Ⅲ)求几何体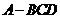 的体积.
的体积.
15.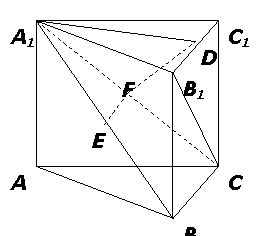 (14分)
(14分) 如图,在直三棱柱
如图,在直三棱柱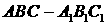 中,
中,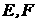 分 别是
分 别是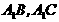 的中点,点
的中点,点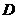 在
在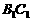 上,
上,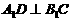
 .学求证:(1)
.学求证:(1)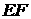 ∥
∥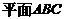
 学科(2)
学科(2)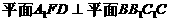

14.若某几何体的三视图(单位: )如图所示,则此几何体的体积是
)如图所示,则此几何体的体积是
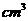 .
.
13.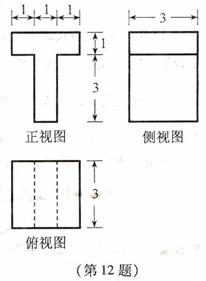 设某几何体的三视图如下(尺寸的长度单位为m)。
设某几何体的三视图如下(尺寸的长度单位为m)。
 则该几何体的体积为
则该几何体的体积为 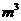

12.如图,已知正三棱柱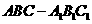 的各条棱长都相等,
的各条棱长都相等,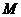 是侧棱
是侧棱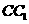 的 中点,则异面直线
的 中点,则异面直线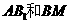 所成的角的大小是
。
所成的角的大小是
。
11.棱长为1cm的小正方体组成如图所示的几何体,
那么这个几何体的表面积是 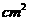
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com