10．(13分)(2010·新疆和田联考)已知函数f(x)＝(m²－m－1)·x^－5m－3，m为何值时，

f(x)：(1)是正比例函数；(2)是反比例函数；

(3)是二次函数；(4)是幂函数．

解　(1)若f(x)是正比例函数，

则－5m－3＝1，解得m＝－，

此时m²－m－1≠0，故m＝－.

(2)若f(x)是反比例函数，则－5m－3＝－1，

则m＝－，此时m²－m－1≠0，故m＝－.

(3)若f(x)是二次函数，则－5m－3＝2，

即m＝－1，此时m²－m－1≠0，故m＝－1，

(4)若f(x)是幂函数，则m²－m－1＝1，

即m²－m－2＝0，解得m＝2或m＝－1.

综上所述，(1)当m＝－时，f(x)是正比例函数．

(2)当m＝－时，f(x)是反比例函数．

(3)当m＝－1时，f(x)是二次函数．

(4)当m＝2或m＝－1时，f(x)是幂函数．

9．(2009·泰安二模)已知(0.7^1.3)^m<(1.3^0.7)^m，则实数m的取值范围是__________．

解析　∵0<0.7^1.3<0.7⁰＝1,1.3^0.7>1.3⁰＝1，

∴0.7^1.3<1.3^0.7.而(0.7^1.3)^m<(1.3^0.7)^m，

∴幂函数y＝x^m在(0，+∞)上单调递增，故m>0.

答案　(0，+∞)

8．(2009·吉林省实验中学一模)函数y＝x+2在区间[0,4]上的最大值M与最小值N的和M

+N＝________.

解析　令t＝∈[0,2]，∴y＝t²+2t＝(t+1)²－1，

在t∈[0,2]上递增．

∴当t＝0时，N＝0，当t＝2时，M＝8.∴M+N＝8.

答案　8

7．(2010·临沂一模)当α∈时，幂函数y＝x^α的图象不可能经过第________象

限．

解析　当x>0时，y>0，故不过第四象限；

当x<0时，y<0或无意义．

故不过第二象限．综上，不过二、四象限．也可画图观察．

答案　二、四

6.(2010·莆田调研)已知函数y＝log(x²－2kx+k)的值域为R，则实数k的取值范围是(　)

A．(0,1)　 　　　　　　　　　　　　　　　　　　 B．(－∞，0]∪[1，+∞)

C．[0,1)　 　　　　　　　　　　　　　　　　　　 D．k＝0或k≥1

解析　要满足题意，t＝x²－2kx+k要能取到所有正实数，抛物线要与坐标轴有交点，

∴Δ＝4k²－4k≥0.解得k≥1或k≤0.

答案　B

5．(2009·山东实验中学第一次诊断)若0<a<1，x>y>1，则下列关系式中正确的个数是(　)

①a^x>a^y　②x^a>y^a　③log_ax>log_ay　④log_xa>log_ya

A．4　 　　　　　　　　　　 B．3 　　　　　　　　　 C．2　 　　　　　　　　 D．1

解析　∵0<a<1，x>y>1，

∴y＝a^x递减，故①不正确；y＝x^a递增，故②正确；

y＝log_ax递减，故③不正确．

∵log_xa<0，log_ya<0，

∴log_xa>log_ya⇔log_ax<log_ay，正确．

综上，②④正确．

答案　C

4．(2009·云浮联考)函数f(x)＝－x²+(2a－1)|x|+1的定义域被分成了四个不同的单调区间，

则实数a的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．a>　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B.<a<

C．a>　 　　　　　　　　　　　　　　　　　　　　　　　　　　 D．a<

解析　f(x)＝－x²+(2a－1)|x|+1是由函数f(x)＝－x²+(2a－1)x+1变化得到，第一步保留y轴右侧的图象，再作关于y轴对称的图象．因为定义域被分成四个单调区间，所以f(x)＝－x²+(2a－1)x+1的对称轴在y轴的右侧，使y轴右侧有两个单调区间，对称后有四个单调区间．所以>0，即a>.

答案　C

3．(2009·湖北理，9)设球的半径为时间t的函数R(t)．若球的体积以均匀速度c增长，则球的表面积的增长速度与球半径　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．成正比，比例系数为c

B．成正比，比例系数为2c

C．成反比，比例系数为c

D．成反比，比例系数为2c

解析　∵V＝πR³(t)，∴V′(t)＝4πR²(t)·R′(t)＝c.

∴R′(t)＝.∵S(t)＝4πR²(t)，

∴S′(t)＝8πR(t)R′(t)＝8πR(t)·＝.

答案　D

2．(2010·淄博一模)函数f(x)＝|x| (n∈N^*，n>9)的图象可能是　　　　　　　　　　　　　　　　 (　)

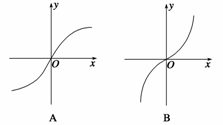
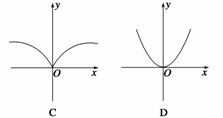
解析　∵f(－x)＝|－x|＝|x|＝f(x)，

∴函数为偶函数，图象关于y轴对称，故排除A、B.

令n＝18，则f(x)＝|x|，当x≥0时，f(x)＝x，由其在第一象限的图象知选C.

答案　C

1．(2009·菏泽重点中学阶段性练习)下列函数：

①y＝；②y＝3x－2；③y＝x⁴+x²；④y＝，

其中幂函数的个数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．1　 　　　　　　　　　　 B．2 　　　　　　　　　 C．3　 　　　　　　　　 D．4

解析　∵①中y＝x^－3；④中y＝x符合幂函数定义；而②中y＝3x－2，③中y＝x⁴+x²不符合幂函数的定义．

答案　B