
题目列表(包括答案和解析)
24.设直线a上有6个点,直线b上有9个点,则这15个点,能确定_____个不同的平面.
解析: 当直线a,b共面时,可确定一个平面; 当直线a,b异面时,直线a与b上9个点可确定9个不同平面,直线b与a上6个点可确定6个不同平面,所以一点可以确定15个不同的平面.
23.OX,OY,OZ是空间交于同一点O的互相垂直的三条直
线,点P到这三条直线的距离分别为3,4,7,则OP长
为_______.
解析:在长方体OXAY-ZBPC中,OX、OY、OZ是相交的三条互相垂直的三条直线。又PZ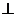 OZ,PY
OZ,PY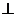 OY,PX
OY,PX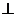 OX,有 OX2+OZ2=49,OY2=OX2=9,
OY2+OZ2=16,
OX,有 OX2+OZ2=49,OY2=OX2=9,
OY2+OZ2=16,
得 OX2+OY2+OZ2=37,OP= .
.
22.
 如图,正四面体
如图,正四面体 (空间四边形的四条边长及两对角线的长都相等)中,
(空间四边形的四条边长及两对角线的长都相等)中, 分别是棱
分别是棱 的中点, 则
的中点, 则
 和
和 所成的角的大小是________.
所成的角的大小是________.
解析:设各棱长为2,则EF= ,取AB的中点为M,
,取AB的中点为M, 即
即
4.2米
解析:树高为AB,影长为BE,CD为树留在墙上的影高, CE=
CE= 米,树影长BE=
米,树影长BE= 米,树高AB=
米,树高AB= BE=
BE= 米。
米。
60. l1、l2是两条异面直线,直线m1、m2与l1、l2都相交,则m1、m2的位置关系是( )
A.异面或平行 B.相交
C.异面 D.相交或异面
解析:D


59. 垂直于同一条直线的两条直线的位置关系是( )
A.平行 B.相交
C.异面 D.以上都有可能
解析:D
58. 已知异面直线 与
与 所成的角为
所成的角为 ,P为空间一定点,则过点P且与
,P为空间一定点,则过点P且与 ,
, 所成的角均是
所成的角均是 的直线有且只有( )
的直线有且只有( )
A、1条 B、2条 C、3条 D、4条
解析: 过空间一点P作 ∥
∥ ,
, ∥
∥ ,则由异面直线所成角的定义知:
,则由异面直线所成角的定义知: 与
与 的交角为
的交角为 ,过P与
,过P与 ,
, 成等角的直线与
成等角的直线与 ,
, 亦成等角,设
亦成等角,设 ,
, 确定平面
确定平面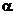 ,
, ,
, 交角的平分线为
交角的平分线为 ,则过
,则过 且与
且与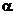 垂直的平面(设为
垂直的平面(设为 )内的任一直线
)内的任一直线 与
与 ,
, 成等角(证明从略),由上述结论知:
成等角(证明从略),由上述结论知: 与
与 ,
, 所成角大于或等于
所成角大于或等于 与
与 ,
, 所成角
所成角 ,这样在
,这样在 内
内 的两侧与
的两侧与 ,
, 成
成 角的直线各有一条,共两条。在
角的直线各有一条,共两条。在 ,
, 相交的另一个角
相交的另一个角 内,同样可以作过
内,同样可以作过 角平分线且与
角平分线且与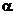 垂直的平面
垂直的平面 ,由上述结论知,
,由上述结论知, 内任一直线与
内任一直线与 ,
, 所成角大于或等于
所成角大于或等于 ,所以
,所以 内没有符合要求的直线,因此过P与
内没有符合要求的直线,因此过P与 ,
, 成
成 的直线有且只有2条,故选(B)
的直线有且只有2条,故选(B)
57. 三棱柱 ,平面
,平面 ⊥平面OAB,
⊥平面OAB,

 ,且
,且 ,求异面直线
,求异面直线 与
与 所成角的大小,(略去了该题的1问)
所成角的大小,(略去了该题的1问)
解析: 在平面 内作
内作 于C ,连
于C ,连 ,
,
由平面 平面AOB,
平面AOB, 知,
知,
AO⊥平面 , ∴
, ∴  ,
,
又  , ∴ BC⊥平面
, ∴ BC⊥平面 ,
,
∴  为
为 在平面
在平面 内的射影。
内的射影。
设 与
与 所成角为
所成角为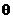 ,
, 与
与 所成角为
所成角为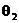 ,
,
则 ,
,
由题意易求得  ,
,
∴  ,
,
在矩形 中易求得
中易求得 与
与 所成角
所成角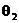 的余弦值:
的余弦值: ,
,
∴  ,
,
即 与
与 所成角为
所成角为  。
。
56.. 在正四面体ABCD中,E,F分别为BC,AD的中点,
求异面直线AE与CF所成角的大小。
解析: 连接BF、EF,易证AD⊥平面BFC,
∴ EF为AE在平面BFC内的射影,
设AE与CF所成角为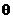 ,
,
 ∴
∴  ,
,
设正四面体的棱长为 ,则
,则 ,
,
显然 EF⊥BC, ∴  ,
,
∴  ,
,  ,
,
∴  , 即AE∴与CF所成角为
, 即AE∴与CF所成角为  。
。
55. 已知平行六面体
已知平行六面体 的底面ABCD是菱形,且
的底面ABCD是菱形,且 ,证明
,证明  。
。
(略去了该题的2,3问)
解析: 设 在平面ABCD内射影为H,则CH为
在平面ABCD内射影为H,则CH为 在平面ABCD内的射影,
在平面ABCD内的射影,
∴  ,
,
∴  ,
,
由题意  , ∴
, ∴ 。
。
又 ∵
∴ , 从而CH为
, 从而CH为 的平分线,
的平分线,
又四边形ABCD是菱形, ∴
∴ 与BD所成角为
与BD所成角为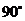 , 即
, 即
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com