
题目列表(包括答案和解析)
26. 在空间四边形ABCD中,E,H分别是AB,AD的中点,F,G分别是CB,CD的中点,若AC + BD = a ,AC
在空间四边形ABCD中,E,H分别是AB,AD的中点,F,G分别是CB,CD的中点,若AC + BD = a ,AC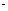 BD =b,求
BD =b,求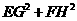 .
.
解析:四边形EFGH是平行四边形,…………(4分)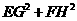 =2
=2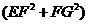 =
=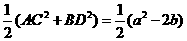
25. 在空间四边形ABCD中,E,F分别是AB,BC的中点.求证:EF和AD为异面直线.
解析:假设EF和AD在同一平面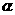 内,…(2分),则A,B,E,F
内,…(2分),则A,B,E,F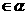 ;……(4分)又A,E
;……(4分)又A,E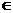 AB,∴AB
AB,∴AB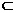
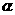 ,∴B
,∴B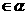 ,……(6分)同理C
,……(6分)同理C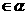 ……(8分)故A,B,C,D
……(8分)故A,B,C,D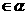 ,这与ABCD是空间四边形矛盾。∴EF和AD为异面直线.
,这与ABCD是空间四边形矛盾。∴EF和AD为异面直线.
24.设直线a上有6个点,直线b上有9个点,则这15个点,能确定_____个不同的平面.
解析: 当直线a,b共面时,可确定一个平面; 当直线a,b异面时,直线a与b上9个点可确定9个不同平面,直线b与a上6个点可确定6个不同平面,所以一点可以确定15个不同的平面.
23.OX,OY,OZ是空间交于同一点O的互相垂直的三条直
线,点P到这三条直线的距离分别为3,4,7,则OP长
为_______.
解析:在长方体OXAY-ZBPC中,OX、OY、OZ是相交的三条互相垂直的三条直线。又PZ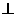 OZ,PY
OZ,PY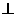 OY,PX
OY,PX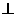 OX,有 OX2+OZ2=49,OY2=OX2=9,
OY2+OZ2=16,
OX,有 OX2+OZ2=49,OY2=OX2=9,
OY2+OZ2=16,
得 OX2+OY2+OZ2=37,OP=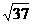 .
.
22.
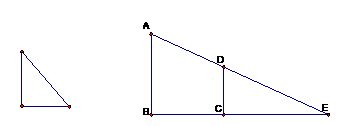 如图,正四面体
如图,正四面体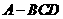 (空间四边形的四条边长及两对角线的长都相等)中,
(空间四边形的四条边长及两对角线的长都相等)中,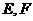 分别是棱
分别是棱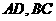 的中点, 则
的中点, 则
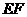 和
和 所成的角的大小是________.
所成的角的大小是________.
解析:设各棱长为2,则EF= ,取AB的中点为M,
,取AB的中点为M,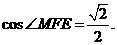 即
即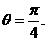
4.2米
解析:树高为AB,影长为BE,CD为树留在墙上的影高,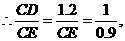 CE=
CE=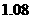 米,树影长BE=
米,树影长BE=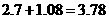 米,树高AB=
米,树高AB= BE=
BE=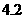 米。
米。
260. .若a、b为异面直线,P为空间一点,过P且与a、b所成角均为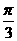 的直线有( )
的直线有( )
A.二条 B.二条或三条
C.二条或四条 D.二条、三条或四条
解析:D
259. 已知异面直线a与b所成的角为50°,P为空间一定点,则过点P且与a、b所成的角都是30°的直线有且仅有( )
A.1条 B.2条 C.3条 D.4条
解析: 过P点分别作直线a′∥a,b′∥b,则a′与b′的夹角为50°,由异面直线所成的角的定义可知,过P点与a′,b′成30°角的条数,就是所求的条数.
画图可知,过P点与a′、b′成30°角的直线只有两条.
∴ 应选B.
258. 在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是( )
A.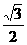 B.
B.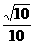 C.
C.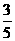 D.
D.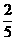

解析:由图所示,AM与CN是异面直线,过N作平行于AM的平行线NP,交AB于P,由定义可知∠PNC就是AM与CN所成的角.因ΔPBC,ΔPBN,ΔCBN皆为直角三角形,且BP=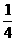 ,BN=
,BN=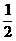 ,BC=1,故PN2=(
,BC=1,故PN2=(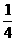 )2+(
)2+(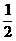 )2=
)2=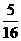 ,CN2=(
,CN2=(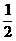 )2+12=
)2+12=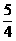 ,PC2=(
,PC2=(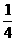 )2+12=
)2+12=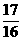 ,在ΔPCN中cos∠PNC=
,在ΔPCN中cos∠PNC=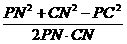 ,所以cos∠PNC=
,所以cos∠PNC=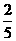 ,因此应选D.
,因此应选D.
257. 如图,ABCD-A1B1C1D1是正方体,B1E1=D1F1=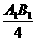 ,则BE1与DF1所成角的余弦值是( )
,则BE1与DF1所成角的余弦值是( )
A.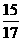 B.
B.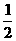 C.
C.
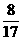 D.
D.
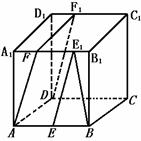
解析:过A点在平面ABB1A1内作AF,使A1F=D1F1,则ADF1F是平行四边形,∴FA∥DF1,再过E1在平面ABB1A1内作E1E∥FA,则∠BE1E即是BE1与DF1所成的角,由已知BE1=DF1=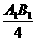 ,ABCD-A1B1C1D1是正方体,∴ E1E=
,ABCD-A1B1C1D1是正方体,∴ E1E=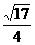 A1B1,
A1B1,
又DF1=AF=E1E,DF1=BE1.
∴
E1E=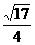 A1B1,EB=
A1B1,EB=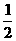 A1B1
A1B1
在ΔBE1E中,cos∠BE1E=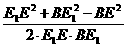 =
=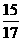 .
.
∴ 应选A.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com