6．为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图如下图，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a，视力在4.6到5.0之间的学生数为b，则a，b的值分别为(　)

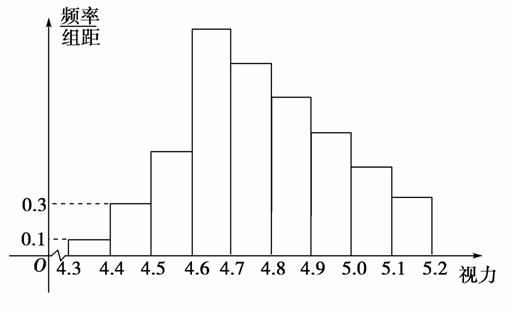
A．0.27,78　 　　　　　　　　　　　B．0.27,83

C．2.7,78 　　　　　　　　　　　　D．2.7,83

解析：选A.组距＝0.1,4.3-4.4之间的频数为100×0.1×0.1＝1.

5．一组数据中的每一个数据都减去80，得一组新数据，若求得新数据的平均数是1.2，方差是4.4，则原来数据的平均数和方差分别是(　)

A．81.2,4.4 　　　　　　　　　　　B．78.8,4.4

C．81.2,84.4　 　　　　　　　　　　D．78.8,75.6

解析：选A.设原来的平均数为.

则－80＝1.2，∴＝81.2，方差不变．

4．如图是甲、乙两名射击运动员各射击10次后所得到的成绩的茎叶图(茎表示成绩的整数环数，叶表示小数点后的数字)，由图可知(　)

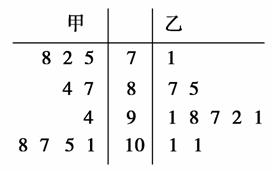
A．甲、乙中位数的和为18.2，乙稳定性高

B．甲、乙中位数的和为17.8，甲稳定性高

C．甲、乙中位数的和为18.5，甲稳定性高

D．甲、乙中位数的和为18.65，乙稳定性高

解析：选A.求中位数时，必须先将这组数据从小到大或从大到小排列，数据的个数为奇数，则中位数是最中间的一个，若数据的个数为偶数，则中位数是最中间的两个数据的平均数，据此易知两人中位数和为18.2，又分析茎叶图可知乙数据分布比较集中，即乙的稳定性较高．

3．在2008年第29届北京奥运会上，我国代表团的金牌数雄踞榜首．如图是位居金牌榜前十二位的代表团获得的金牌数的茎叶图，则这十二个代表团获得的金牌数的平均数与中位数的差m的值为(　)

A．3.5 　　　　　　　　　　B．4

C．4.5 　　　　　　　　　　D．5

解析：选B.由茎叶图中的数据可求得这十二个代表团获得的金牌数的平均数为17.5，中位数为13.5，故m＝4.

2．一个样本数据按从小到大的顺序排列为13,14,19，x,23,27,28,31，其中位数为22，则x等于(　)

A．21 　　　　　　　　　　B．22

C．23　 　　　　　　　　　　D．24

解析：选A.个数为偶数，因此中位数22＝，

∴x＝21.

1.某地一种植物一年生长的高度如下表：

则该植物一年生长在[30,40)内的频率是(　)

A．0.80　　　　　B．0.65

C．0.40　 　　　　　　　　　D．0.25

解析：选C.由频率含义可计算其结果．由频率的定义得80÷(20+30+80+40+30)＝0.40.

6．为了了解九年级学生中女生的身高(单位：cm)情况，某中学对九年级女生身高进行了一次测量，所得数据整理后列出了频率分布表如下：

(1)求出表中m，n，M，N所表示的数分别是多少？

(2)画出频率分布直方图；

(3)全体女生中身高在哪组范围内的人数最多？估计九年级学生中女生的身高在161.5以上的概率．

解：(1)M＝＝50，m＝50－(1+4+20+15+8)＝2，N＝1，n＝＝＝0.04.

(2)作出直角坐标系，组距为4，纵轴表示频率/组距，横轴表示身高，画出直方图如下图．

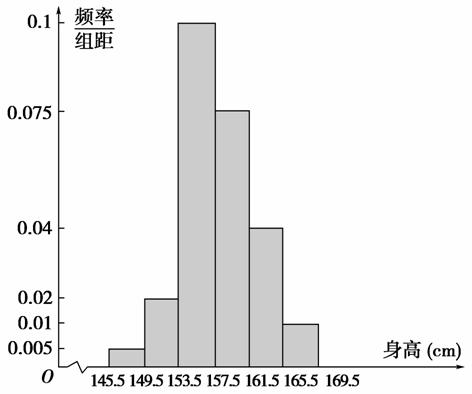
(3)在153.5-157.5范围内最多，估计身高在161.5以上的概率为

P＝＝0.2.

练习

5．(2009年高考重庆卷)从一堆苹果中任取5只，称得它们的质量为(单位：克)：125　124　121　123　127

则该样本标准差s＝________(克)(用数字作答)．

解析：∵＝(125+124+121+123+127)＝124，

∴s²＝[(125－124)²+(124－124)²+(121－124)²+(123－124)²+(127－124)²]＝4，∴s＝2.

答案：2

4．(原创题)在样本的频率分布直方图中，共有4个小长方形，这4个小方形的面积由小到大构成等差数列{a_n}，已知a₂＝2a₁，且样本容量为400，则小长方形面积最大的一组的频数为________．

答案：160

3．为了了解一片经济林的生长情况，随机测量了其中100株树木的底部周长(单位：cm)．根据所得数据画出样本的频率分布直方图(如图)，那么在这100株树木中，底部周长小于110 cm的株数是(　)

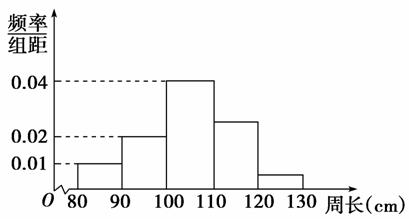
A．30　 　　　　　　　　　B．60

C．70 　　　　　　　　　　D．80

解析：选C.底部周长小于110 cm的频率：

10×0.01+10×0.02+10×0.04＝0.7.

周长小于110 cm的株数为：100×0.7＝70.