
题目列表(包括答案和解析)
3.将容量为100的样本数据,按照从小到大的顺序分为8个组,如下表:
|
组号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
频数 |
x |
13 |
y |
14 |
z |
13 |
12 |
8 |
已知第1小组的频数是第3和第5小组的频数之和,第3小组的频率是第5小组的频率的三倍,则第3小组的频率为
( )
A.0.10 B.0.05
C.0.15 D.0.20
解析:根据题意,得
解得,所以第3组的频率为=0.15.
答案:C
2.采用简单随机抽样从个体数为6的总体中抽取一个容量为3的样本,则对于总体中指定的个体a前两次未被抽到,第三次恰好被抽到的概率为
( )
A. B.
C. D.
解析:解法1:对于从6个个体中抽取1个,每个个体被抽到的概率均为.
解法2:P==.
答案:A
1.某地区有300家商店,其中大型商店30家,中型商店75家,小型商店175家,为了掌握各商店的营业情况,要从中抽取一个容量为20的样本.若采用分层抽样的方法,抽到的中型商店数是
( )
A.2 B.3
C.5 D.13
解析:根据分层抽样按比例抽取,抽取的比例为=,抽取的中型商店数为75×=5.
答案:C
12.设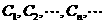 是坐标平面上的一列圆,它们的圆心都在
是坐标平面上的一列圆,它们的圆心都在 轴的正半轴上,且都与直线
轴的正半轴上,且都与直线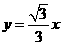 相切,对每一个正整数
相切,对每一个正整数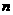 ,圆
,圆 都与圆
都与圆 相互外切,以
相互外切,以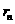 表示
表示 的半径,已知
的半径,已知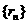 为递增数列.
为递增数列.
 (Ⅰ)证明:
(Ⅰ)证明: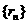 为等比数列;
为等比数列;
(Ⅱ)设 ,求数列
,求数列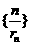 的前
的前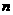 项和.
项和.

13 已知函数f(x)对任意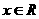 都有
都有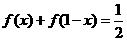 ,(1)求
,(1)求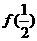 的值
的值
(2)若数列{an}满足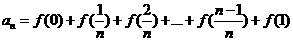 ,求
,求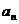
(3)设 ,
,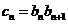 ,求数列
,求数列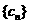 的前n项的和
的前n项的和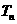
(1) 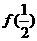 =
= (2)
(2)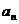 =
= (n+1) (3)
(n+1) (3)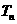 =
=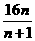
14 已知函数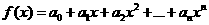 ,且
,且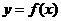 的图像过点
的图像过点 ,且数列{an}为等差数列,
,且数列{an}为等差数列,
(1)求数列{an}的通项公式;(2)当n为奇数时,设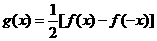 是否存在自然数m和M,使得不等式
是否存在自然数m和M,使得不等式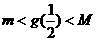 恒成立?若存在,求M-m的最小值,若不存在,说明理由。
恒成立?若存在,求M-m的最小值,若不存在,说明理由。
(1)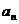 =2n-1 (2)M-m的最小值为2
=2n-1 (2)M-m的最小值为2
18.已知数列{an}中,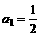 . 点(n, 2an+1
– an)在直线y = x上,其中n = 1,2,3….
. 点(n, 2an+1
– an)在直线y = x上,其中n = 1,2,3….
(1)令bn = an+1 – an – 1,求证数列{bn}是等比数列; (2)求数列{an}的通项;
(3)设Sn、Tn分别为数列{an}、{bn}的前n项和. 是否存在实数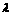 ,使得数列
,使得数列 为等差数列?若存在,试求出
为等差数列?若存在,试求出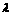 ;若不存在,则说明理由.
;若不存在,则说明理由.
[解析](1)由已知得 ,∴
,∴ ,
,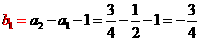 ,
,
又bn = an+1 – an
– 1,∴bn+1 = an+2
– an+1 – 1,∴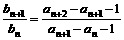
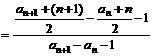
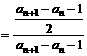
 . ∴{bn}是以
. ∴{bn}是以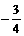 为首项,以
为首项,以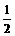 为公比的等比数列.
为公比的等比数列.
(2)由(1)知, =
= ,∴
,∴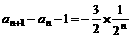 ,∴
,∴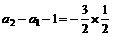 ,
,
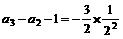 ,…… ∴
,…… ∴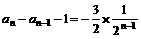 , 将以上各式相加得:
, 将以上各式相加得:
 =
=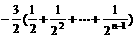 , ∴
, ∴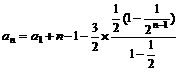 =
=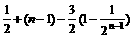 =
= .
.
∴ .
.
(3)解法一:存在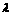 =2,使数列
=2,使数列 是等差数列. ∵Sn = a1 + a1 +…+an
是等差数列. ∵Sn = a1 + a1 +…+an
= + (1 + 2 +…+ n) – 2n =
+ (1 + 2 +…+ n) – 2n =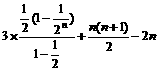 =
= =
=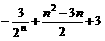 .
.
Tn = b1
+ b +…+bn
=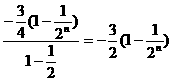 =
= .
.
数列 是等差数列的充要条件是
是等差数列的充要条件是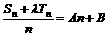 ,(A、B是常数) 即
,(A、B是常数) 即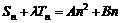 ,
,
又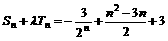 +
+ =
=
∴当且仅当 0,即
0,即 时,数列
时,数列 是等差数列.
是等差数列.
解法二:存在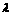 =2,使数列
=2,使数列 是等差数列. 由(1)、(2)知,an + 2bn = n – 2,
是等差数列. 由(1)、(2)知,an + 2bn = n – 2,
∴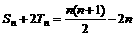 . ∴
. ∴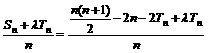 =
= .
.
又Tn = b1 + b2 +…+bn =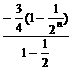 =
=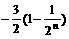 =
= . ∴
. ∴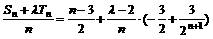 .
.
∴当且仅当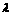 =2时,数列
=2时,数列 是等差数列.
是等差数列.
17.已知数列{an}满足a1=4,an=4-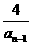 (n≥2),令bn=
(n≥2),令bn= ,
,
(1)求证数列{bn}是等差数列; (2)求数列{an}的通项公式.
(1)[证明] an+1-2=2-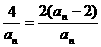 ∴
∴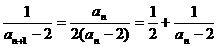 (n≥1)
(n≥1)
故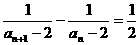 (n≥1) 即bn+1-bn=
(n≥1) 即bn+1-bn=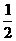 (n≥1) ∴数列{bn}是等差数列.
(n≥1) ∴数列{bn}是等差数列.
(2)[解] ∵{ }是等差数列 ∴
}是等差数列 ∴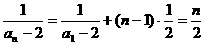 ∴an=2+
∴an=2+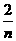
∴数列{an}的通项公式an=2+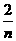
16.已知数列{an}的前n项和是Sn=32n-n2,求数列{|an|}的前n项和Sn′.
[解] ∵a1=S1=32×1-12=31,
当n≥2时,an=Sn-Sn-1=33-2n,
又由an>0,得n<16.5,
即{an}前16项为正,以后皆负.
∴当n≤16时,Sn′=|a1|+|a2|+…+|an|
=a1+a2+…+an=33n-n2.
当n>16时,Sn′=a1+a2+…+a16-a17-a18-…-an=S16-(Sn-S16)=2S16-Sn
=512-32n+n2.
∴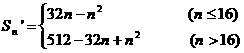
15.设 =
=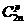
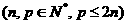 ,数列
,数列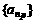 满足
满足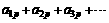
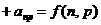 ,则数列
,则数列 的通项公式是
的通项公式是 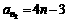 .
.
[思路分析]:令 则
则 ,
,
则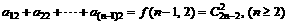 ,两式相减得:
,两式相减得: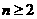 时,
时,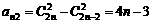 ,且
,且 ,∴
,∴ .
.
14.等差数列{an}中,S 2 = S19且公差d<0,当n = 10或11 时,Sn最大.
13.已知等差数列{an}中,前三项之和为6,末三项和60,Sn = 231,则n = 21 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com