
题目列表(包括答案和解析)
1.这类应用题一般可转化为等差数列或等比数列问题.但在求解过程中,务必“卡手指”,细心计算“年限”.对于“森林木材”既增长又砍伐的问题,则常选用“统一法”统一到“最后”解决.
6.通项转换法:先对通项进行变形,发现其内在特征,再运用分组求和法求和。如
①求数列1×4,2×5,3×6,…,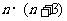 ,…前
,…前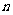 项和
项和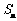 =
=
(答: );
);
②求和:
(答: )
)
5.裂项相消法:如果数列的通项可“分裂成两项差”的形式,且相邻项分裂后相关联,那么常选用裂项相消法求和.常用裂项形式有:
①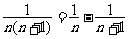 ; ②
; ②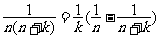 ;
;
③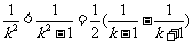 ,
, ;
;
④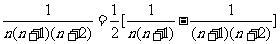 ;⑤
;⑤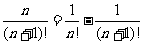 ;
;
⑥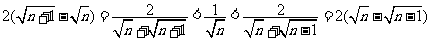 .
.
如(1)求和: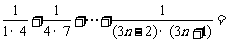
(答: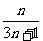 );
);
(2)在数列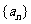 中,
中,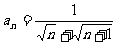 ,且Sn=9,则n=_____
,且Sn=9,则n=_____
(答:99);
4.错位相减法:如果数列的通项是由一个等差数列的通项与一个等比数列的通项相乘构成,那么常选用错位相减法(这也是等比数列前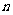 和公式的推导方法).
和公式的推导方法).
如(1)设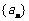 为等比数列,
为等比数列,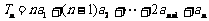 ,已知
,已知 ,
,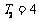 ,①求数列
,①求数列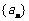 的首项和公比;②求数列
的首项和公比;②求数列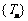 的通项公式.(答:①
的通项公式.(答:①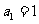 ,
,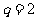 ;②
;②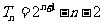 );
);
(2)设函数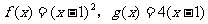 ,数列
,数列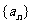 满足:
满足: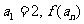
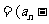
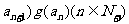 ,①求证:数列
,①求证:数列 是等比数列;②令
是等比数列;②令
 ,求函数
,求函数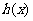 在点
在点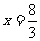 处的导数
处的导数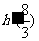 ,并比较
,并比较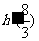 与
与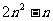 的大小。(答:①略;②
的大小。(答:①略;②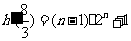 ,当
,当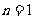 时,
时,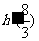 =
=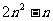 ;当
;当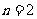 时,
时,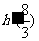 <
<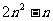 ;当
;当 时,
时,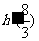 >
>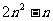 )
)
3.倒序相加法:若和式中到首尾距离相等的两项和有其共性或数列的通项与组合数相关联,则常可考虑选用倒序相加法,发挥其共性的作用求和(这也是等差数列前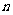 和公式的推导方法). 如
和公式的推导方法). 如
①求证: ;
;
②已知 ,则
,则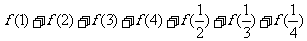 =______
=______
(答: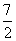 )
)
2.分组求和法:在直接运用公式法求和有困难时,常将“和式”中“同类项”先合并在一起,再运用公式法求和. 如求: (答:
(答: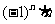 )
)
1.公式法:①等差数列求和公式;②等比数列求和公式,特别声明:运用等比数列求和公式,务必检查其公比与1的关系,必要时需分类讨论.;③常用公式: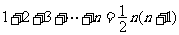 ,
,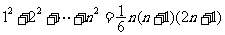 ,
,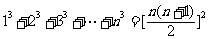 .如
.如
(1)等比数列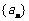 的前
的前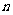 项和Sn=2n-1,则
项和Sn=2n-1,则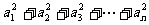 =_____
=_____
(答: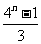 );
);
(2)计算机是将信息转换成二进制数进行处理的。二进制即“逢2进1”,如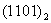 表示二进制数,将它转换成十进制形式是
表示二进制数,将它转换成十进制形式是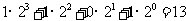 ,那么将二进制
,那么将二进制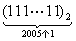 转换成十进制数是_______
转换成十进制数是_______
(答: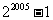 )
)
⑴公式法:①等差数列通项公式;②等比数列通项公式。如已知数列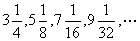 试写出其一个通项公式:__________
试写出其一个通项公式:__________
(答: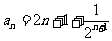 )
)
⑵已知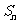 (即
(即 )求
)求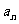 ,用作差法:
,用作差法: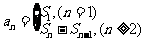 。如
。如
①已知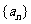 的前
的前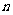 项和满足
项和满足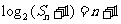 ,求
,求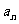
(答: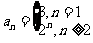 );
);
②数列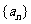 满足
满足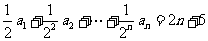 ,求
,求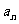
(答: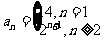 )
)
⑶已知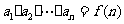 求
求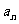 ,用作商法:
,用作商法: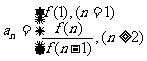 。如数列
。如数列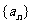 中,
中,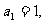 对所有的
对所有的 都有
都有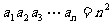 ,则
,则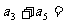 ______
______
(答: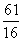 )
)
⑷若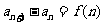 求
求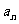 用累加法:
用累加法: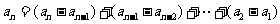

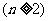 。如已知数列
。如已知数列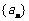 满足
满足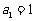 ,
,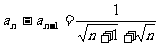
 ,则
,则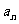 =________
=________
(答: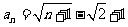 )
)
⑸已知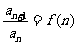 求
求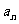 ,用累乘法:
,用累乘法: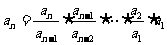
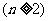 。如已知数列
。如已知数列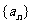 中,
中,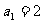 ,前
,前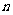 项和
项和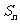 ,若
,若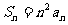 ,求
,求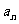
(答: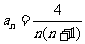 )
)
⑹已知递推关系求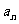 ,用构造法(构造等差、等比数列)。特别地,(1)形如
,用构造法(构造等差、等比数列)。特别地,(1)形如 、
、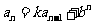 (
(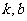 为常数)的递推数列都可以用待定系数法转化为公比为
为常数)的递推数列都可以用待定系数法转化为公比为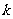 的等比数列后,再求
的等比数列后,再求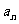 。如①已知
。如①已知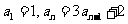 ,求
,求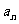 (答:
(答: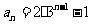 );②已知
);②已知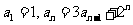 ,求
,求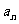 (答:
(答: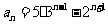 );(2)形如
);(2)形如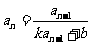 的递推数列都可以用倒数法求通项。如①已知
的递推数列都可以用倒数法求通项。如①已知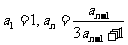 ,求
,求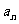 (答:
(答: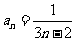 );②已知数列满足
);②已知数列满足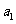 =1,
=1,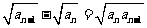 ,求
,求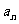 (答:
(答: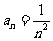 )
)
注意:(1)用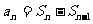 求数列的通项公式时,你注意到此等式成立的条件了吗?(
求数列的通项公式时,你注意到此等式成立的条件了吗?(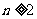 ,当
,当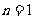 时,
时,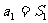 );(2)一般地当已知条件中含有
);(2)一般地当已知条件中含有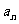 与
与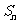 的混合关系时,常需运用关系式
的混合关系时,常需运用关系式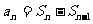 ,先将已知条件转化为只含
,先将已知条件转化为只含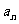 或
或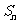 的关系式,然后再求解。如数列
的关系式,然后再求解。如数列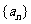 满足
满足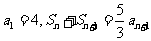 ,求
,求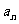 (答:
(答: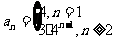 )
)
16.定义在R上的单调递减函数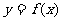 满足
满足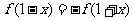 ,且对于任
,且对于任
意 ,不等式
,不等式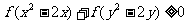 恒成立,则当
恒成立,则当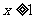 时,
时,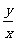 的取
的取
15.已知中心在原点,焦点在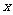 轴上的双曲线的一条渐近线方程为
轴上的双曲线的一条渐近线方程为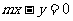 ,
,
若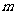 在集合
在集合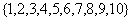 中任意取一个值,则双曲线的离心率大于3的
中任意取一个值,则双曲线的离心率大于3的
概率是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com