
题目列表(包括答案和解析)
(二)选做题(14-15题,考生只能从中选做一题)
14、 已知直线L的极坐标方程为:
已知直线L的极坐标方程为: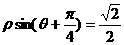 ,
,
则极点到直线L的距离为 _____________;
15、如图,已知⊙O的直径AB与弦AC的夹角为30°,
过C的切线PC与AB延长线交于P,若PC=5,则⊙O的半径为______。
广东省崇雅中学2011届文科数学基础训练05
一 选择题(每题5分,共计50分)
1、设全集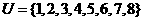 ,集合
,集合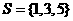 ,
,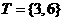 ,则
,则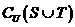 等于( )
等于( )
A.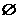 B.
B.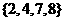 C.
C.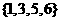 D.
D.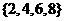
2、在复平面内,复数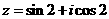 对应的点位于( )
对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3、“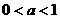 ”是“直线
”是“直线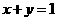 与圆
与圆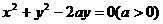 没有公共点”的( )
没有公共点”的( )
A 充要条件 B 充分不必要条件
C 必要不充分条件 D 既不充分又不必要条件
4、设等比数列{ 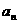 }的前n 项和为
}的前n 项和为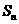 ,若
,若 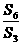 =3 ,则
=3 ,则 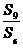 =
= 

A
2
B
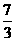 C
C 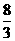 D 3
D 3
5、已知函数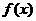 在R上满足
在R上满足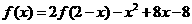 ,则曲线
,则曲线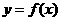 在点
在点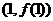 处的切线方程是
处的切线方程是
(A)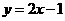 (B)
(B)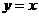 (C)
(C)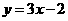 (D)
(D)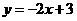

6、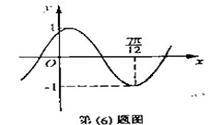 将函数
将函数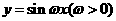 的图象按向量
的图象按向量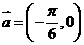 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
A.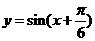 B.
B.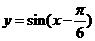
C.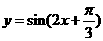 D.
D.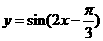
7、把一根1米长的绳子剪成两段,其中一段小于0.4米的概率是( )
A 0.2 B 0.4 C 0.6 D 0.8
8、若抛物线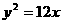 的焦点与双曲线
的焦点与双曲线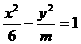 的右焦点重合,则双曲线的渐近线为( )
的右焦点重合,则双曲线的渐近线为( )
A.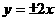 B.
B.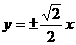 C.
C.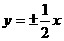 D.
D.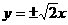
9、已知非零向量与满足(+)·=0且·= , 则△ABC为( )
A.三边均不相等的三角形 B.直角三角形
C.等腰非等边三角形 D.等边三角形
10、平行四边形的一个顶点A在平面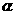 内,其余顶点在
内,其余顶点在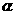 的同侧,已知其中有两个顶点到
的同侧,已知其中有两个顶点到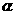 的距离分别为1和2 ,那么剩下的一个顶点到平面
的距离分别为1和2 ,那么剩下的一个顶点到平面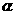 的距离可能是( )
的距离可能是( )
A 1或3 B 2或4 C 1或4 D 2或3
二 填空题
11、若实数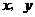 满足
满足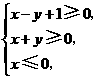 则
则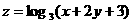 的最小值是________;
的最小值是________;
12、 下列程序运行的结果是___________;
|
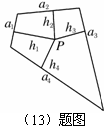
13、如图所示,面积为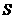 的平面凸四边形的第
的平面凸四边形的第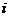 条边的边长记为
条边的边长记为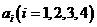 ,此四边形内任一点
,此四边形内任一点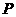 到第
到第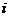 条边的距离记为
条边的距离记为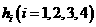 ,若
,若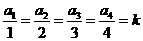 ,
,
则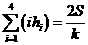 .类比以上性质,体积为
.类比以上性质,体积为 的三棱锥的第
的三棱锥的第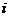 个面的面积记为
个面的面积记为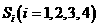 , 此三棱锥内任一点
, 此三棱锥内任一点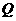 到第
到第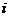 个面的距离记为
个面的距离记为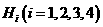 ,若
,若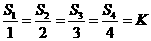 , 则
, 则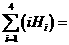 ________.
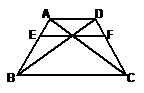
14、如下图,在梯形ABCD中,AD//BC,BD、AC相交于O,过O的直线分别交AB、CD于E、F,且EF//BC,若AD=12,BC=20,则EF=
.
________.
14、如下图,在梯形ABCD中,AD//BC,BD、AC相交于O,过O的直线分别交AB、CD于E、F,且EF//BC,若AD=12,BC=20,则EF=
.
|
15、在极坐标系中,圆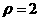 上的点到直线
上的点到直线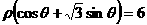 的距离的最小值是 .
的距离的最小值是 .
16、已知二次函数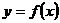 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为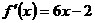 .数列
.数列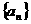 的前
的前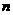 项和为
项和为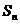 ,点
,点 均在函数
均在函数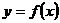 的图像上.
的图像上.
(Ⅰ)求数列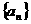 的通项公式;
的通项公式;
(Ⅱ)设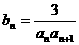 ,
,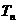 是数列
是数列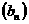 的前
的前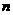 项和,求使得
项和,求使得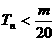 对所有
对所有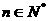 都成立的最小正整数
都成立的最小正整数 .
.
广东省崇雅中学2011届文科数学基础训练06
一 选择题(每题5分,共计50分)
1、已知全集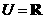 ,集合
,集合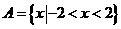 ,
,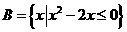 ,则
,则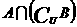 =( )
=( )
A.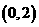 B.
B.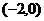 C.
C.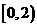 D.
D.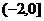
2、复数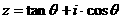 对应的点在第二象限(其中
对应的点在第二象限(其中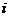 为虚数单位),则θ的终边位于( )
为虚数单位),则θ的终边位于( )
A 第一象限 B 第二象限 C 第三象限 D 第四象限
3、为迎接“国际三八妇女节”,惠阳区教育局于3月4日在我校成功了举办“教育女人最美丽”暨第一届健美操大赛。9位评委给崇雅代表队打出的分数如茎叶图所示,统计员
 在去掉一个最高分和一个最低分后,算得平均分为91,
在去掉一个最高分和一个最低分后,算得平均分为91,
复核员在复核时,发现有一个数字(茎叶图中的x)无法
看清,若记分员计算无误,则数字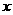 应该是( )
应该是( )
A.2 B.3 C.4 D.5
4、已知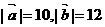 且
且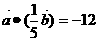 ,则
,则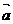 与
与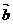 的夹角为(
)
的夹角为(
)
A 600 B 1200 C 1350 D 1500
5、把函数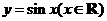 的图象上所有的点向左平行移动
的图象上所有的点向左平行移动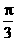 个单位长度,再把所得图象上所有点的横坐标缩短到原来的
个单位长度,再把所得图象上所有点的横坐标缩短到原来的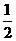 倍(纵坐标不变),得到的图象所表示的函数是( )
倍(纵坐标不变),得到的图象所表示的函数是( )
A.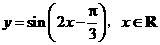 B.
B.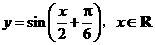
C. 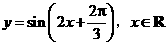 D.
D.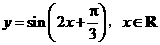
6、已知曲线y=x 2-1与y=1-x3在点x 0处的切线平行,则x 0的值为( )
A 0
B -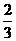 C 0或-
C 0或-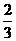 D 0或1
D 0或1
7、已知直线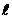 ⊥平面α,直线m
⊥平面α,直线m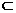 平面β,下列四个命题:
平面β,下列四个命题:
① α∥β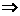
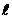 ⊥m ② α⊥β
⊥m ② α⊥β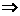
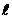 ∥m ③
∥m ③ 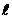 ∥m
∥m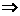 α⊥β ④
α⊥β ④ 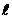 ⊥m
⊥m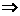 α∥β
α∥β
其中正确的命题是( )
A ①② B ③④ C ②④ D ①③
8、已知函数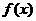 是
是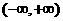 上的偶函数,若对于
上的偶函数,若对于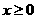 ,都有
,都有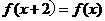 ,且当
,且当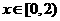 时,
时,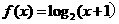 ,则
,则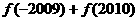 的值为
的值为
A.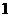 B.
B.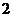 C.
C.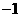 D.
D. 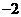
9、设等差数列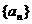 满足
满足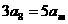 ,
,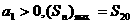 ,则m的值为( )
,则m的值为( )
A 14 B 13 C 12 D 11
10、设P是△ABC内任意一点,S△ABC表示△ABC的面积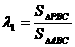 ,
,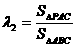 ,
,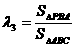 ,定义
,定义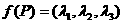 ,若G是△ABC的重心,
,若G是△ABC的重心,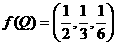 ,则( )
,则( )
A 点Q在△GAB内 B 点Q在△GAC内 C 点Q在△GCB内 D 点Q与点G重合
二 填空题本大题共5小题,考生作答4小题,每小题5分,满分20分。
11、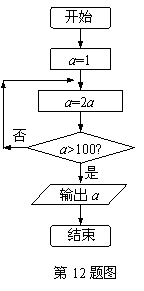 若抛物线
若抛物线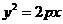 的焦点与双曲线
的焦点与双曲线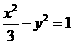 的右焦点重合,则
的右焦点重合,则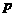 的值
的值
12、程序框图(即算法流程图)如右图所示,其输出结果是
13、2008年5月12日14时28分04秒四川省汶川发生8.0特大地震;2010年1月12日16时53分(北京时间13日5时53分)加勒比岛国海地当地时间发生里氏7.0级地震; 2010年2月27日14分,智利第二大城市康塞普西翁发生里氏8.8级特大地震,给人民生命财产造成巨大损失。
里氏地震等级最早是在1935年由美国加州理工学院的地震学家里特制定的,它同震源中心释放的能量(热能和动能)大小有关。震级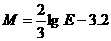 ,其中E(焦耳)为地震时以地震波的形式释放能量。如果里氏6.0级地震释放的能量相当于1颗美国在二战投放在广岛的原子弹的能量,那么汶川大地震所释放的能量相当于________颗广岛原子弹。
,其中E(焦耳)为地震时以地震波的形式释放能量。如果里氏6.0级地震释放的能量相当于1颗美国在二战投放在广岛的原子弹的能量,那么汶川大地震所释放的能量相当于________颗广岛原子弹。
14、 (坐标系与参数方程选做题)
曲线
(坐标系与参数方程选做题)
曲线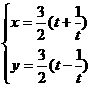 ( t为参数,t≠0)的离心率为 。
( t为参数,t≠0)的离心率为 。
15、几何证明选讲)如图,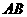 为⊙
为⊙ 的直径,弦
的直径,弦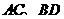 交
交
于点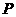 ,若
,若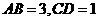 , 则
, 则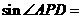 .
.
16、如图,在长方体 中,
中,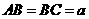 ,
,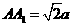 ,点
,点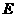 是棱
是棱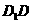 的中点,M为
的中点,M为 。
。
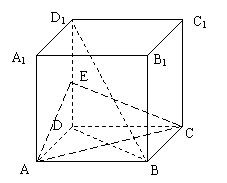 (1)画出几何体ABCEA1B1C1D1的主视图和左视图
(1)画出几何体ABCEA1B1C1D1的主视图和左视图
(2)求证:BD1∥平面ACE
(3)求三棱锥M-ACE的体积
广东省崇雅中学2011届文科数学基础训练07
一 选择题(每题5分,共计50分)
1、集合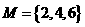 的真子集的个数为( )
的真子集的个数为( )
A.6 B.7 C.8 D.9
2、“m=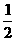 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的(
)。
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的(
)。
A.充分必要条件 B.充分而不必要条件
C..必要而不充分条件 D.既不充分也不必要条件
3、已知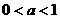 ,
,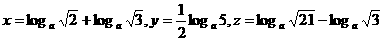 ,则( )
,则( )
A. x>y>z B z>y>x C y>x>z D z>x>y
4、下列函数图象中,正确的是( ).


5、已知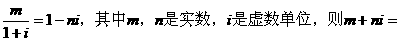 ( )
( )
(A)1+2i (B) 1-2i (C) 2+i (D)2-i
6、设函数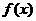 定义如下表,数列
定义如下表,数列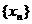 满足
满足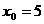 ,且对任意自然数
,且对任意自然数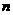 都有
都有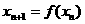 ,则
,则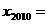
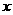 |
1 |
2 |
3 |
4 |
5 |
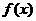 |
4 |
1 |
3 |
5 |
2 |
 A.1
B.2 C.4
D.5
A.1
B.2 C.4
D.5
7、已知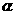 ,
,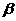 是平面,
是平面, ,
,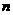 是直线,给出下列命题
是直线,给出下列命题
①若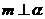 ,
,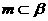 ,则
,则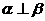 .
.
②若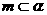 ,
,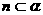 ,
,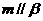 ,
,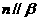 ,则
,则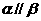 .
.
③如果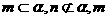 、n是异面直线,那么
、n是异面直线,那么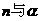 相交.
相交.
④若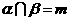 ,
,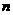 ∥
∥ ,且
,且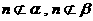 ,则
,则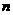 ∥
∥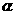 且
且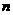 ∥
∥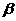 .
.
其中正确命题的个数是
A.4 B.3 C.2 D.1
8、设椭圆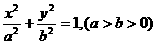 的离心率为
的离心率为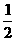 ,右焦点为
,右焦点为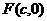 ,
,
方程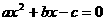 的两个实根分别为
的两个实根分别为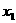 和
和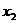 ,则点
,则点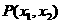
A 必在圆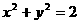 内 B 必在圆
内 B 必在圆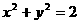 上
上
C 必在圆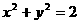 外 D 以上都有可能
外 D 以上都有可能
9、在电脑游戏中,“主角”的生命机会往往被预先设定。如某枪战,“主角”被设置生命6次,每次生命承受射击8次(即被击中8次就失去一次生命机会),假设射击为单发射击,如图是为“主角”耗用生命机会的过程设计的一个程序框图,请问判断框内应该填( )
A i<6 B i<8 C i>48 D i<48
 10、一个盒子装有六张卡片,上面分别写着如下定义域为R的函数:
10、一个盒子装有六张卡片,上面分别写着如下定义域为R的函数: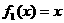 ,
,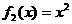 ,
,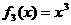 ,
, 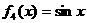 ,
,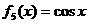 ,
,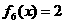 。从盒子
。从盒子
中任取两张卡片,将卡片上的函数相加
得到一个新函数是奇函数的概率为( )
A 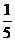 B
B 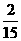 C
C 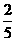 D
D 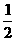
二 填空题(每题5分,共计20分)
11、已知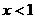 ,函数
,函数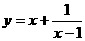 的最大值是___________;
的最大值是___________;
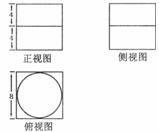
12、下图是一个物体的三视图,根据图中尺寸(单位:cm),可求得该物体的体积为 cm3;
13、关于函数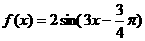 ,有下列命题:① 其最小正周期为
,有下列命题:① 其最小正周期为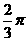 ;② 其图象可由
;② 其图象可由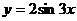 的图象向左平移
的图象向左平移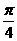 个单位得到;③ 其表达式可改写为
个单位得到;③ 其表达式可改写为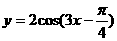 ;④ 在
;④ 在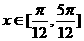 上为增函数;⑤ 其图象关于点
上为增函数;⑤ 其图象关于点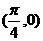 成中心对称。其中正确的有______(请把正确的序号都填上)
成中心对称。其中正确的有______(请把正确的序号都填上)
14、已知圆C的参数方程为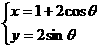 (
(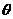 为参数),P是圆C与y轴的交点,若以圆心C为极点,x 轴的正半轴为极轴建立极坐标系,则过点P的圆切线的极坐标方程是
.
为参数),P是圆C与y轴的交点,若以圆心C为极点,x 轴的正半轴为极轴建立极坐标系,则过点P的圆切线的极坐标方程是
.
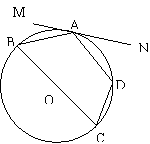
15、如图,四边形ABCD内接于⊙ ,BC是直径,MN切⊙
,BC是直径,MN切⊙ 于A,
于A,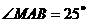 ,则
,则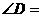 .
.
16、联想集团惠州分公司生产某种芯片,根据历年的情况知,生产这种芯片每天的固定成本为14000元,每天生产一件产品,成本增加210元。已知该产品的日销售量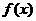 与产量x之间的函数关系式为
与产量x之间的函数关系式为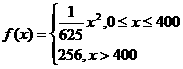 ,每个芯片的售价
,每个芯片的售价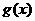 与产量x之间的关系式为
与产量x之间的关系式为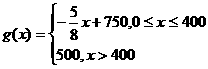
① 写出该公司的日销售利润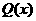 与产量x之间的关系式;
与产量x之间的关系式;
② 若要使得日销售利润最大,每天该生产多少件产品,并求最大利润。
广东省崇雅中学2011届文科数学基础训练08
一 选择题(每题5分,共计50分)
1、已知集合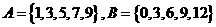 ,则
,则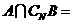
(A) 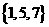 (B)
(B)
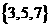 (C)
(C)  (D)
(D) 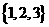
2、复数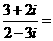 (
)
(
)
(A)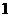 (B)
(B)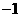 (C)
(C)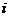 (D)
(D)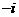
3、w.w. 若等差数列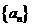 的前5项和
的前5项和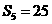 ,且
,且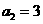 ,则
,则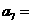 ( )
( )
A.12 B.13 C.14 D.15
4、已知α,β表示两个不同的平面,m为平面α内的一条直线,则“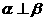 ”是“
”是“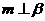 ”的(
)
”的(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件w.
5、若直线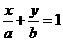 与圆
与圆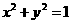 有公共点,则( )
有公共点,则( )
A.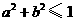 B.
B.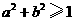 C.
C.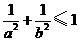 D.
D.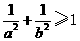
6、甲、乙、丙三名同学站成一排,甲站在中间的概率是( )
A 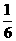 B
B 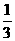 C
C 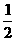 D
D 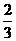
7、四边形ABCD的对角线AC与BD交于O,若△COD与△AOB的面积分别为4和9,则四边形ABCD的面积最小值为( )
A 18 B 20 C 25 D 26
8、已知O,N,P在 所在平面内,且
所在平面内,且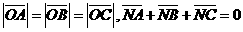 ,且
,且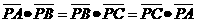 ,则点O,N,P依次是
,则点O,N,P依次是 的
的
(A)重心 外心 垂心 (B)重心 外心 内心
(C)外心 重心 垂心 (D)外心 重心 内心
(注:三角形的三条高线交于一点,此点为三角形的垂心)
9、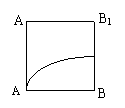
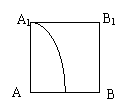
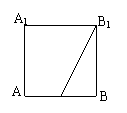
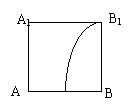 正方体
正方体 中,在侧面
中,在侧面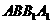 内有一动点
内有一动点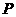 ,它到直线
,它到直线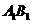 与到直线
与到直线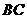 的距离相等,则点
的距离相等,则点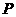 的轨迹是下图中的
的轨迹是下图中的
10、在R上定义运算⊙: 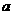 ⊙
⊙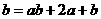 ,则满足
,则满足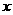 ⊙
⊙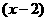 <0的实数
<0的实数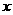 的取值范围为( ).
的取值范围为( ).
A.(0,2)
B.(-2,1) C. D.(-1,2)
D.(-1,2)
(一)必做题(11-13题)
11、.为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了下表:
|
|
喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
男生 |
20 |
5 |
25 |
|
女生 |
10 |
15 |
25 |
|
合计 |
30 |
20 |
50 |
下面的临界值表供参考:
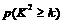 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
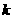 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
则根据以下参考公式可得随机变量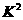 的值为 、(保留三位小数)有 %.
的值为 、(保留三位小数)有 %.
的把握认为喜爱打篮球与性别有关.
 (参考公式:
(参考公式: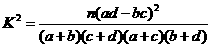 ,其中
,其中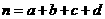 )
)
12、在△ABC中,把正弦定理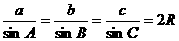
代入余弦定理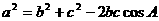 得公式:
得公式:
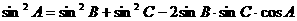 。
。
利用上述关系式计算:
 ;
;
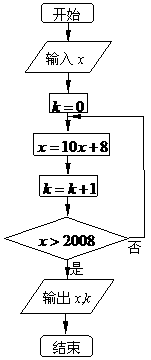
13、按如图所示的程序框图运算.
(1)
若输入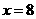 ,则输出
,则输出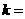 ;
;
(2) 若输出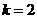 ,则输入
,则输入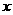 的取值范围是
.
的取值范围是
.
10、.已知函数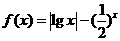 有两个零点
有两个零点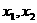 ,则有
,则有
A. 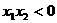 B.
B.
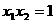 C.
C. 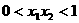 D.
D. 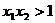
9、水平地面上A、B两地立有高分别20米和40米的旗杆,地面上P对两旗杆顶端的仰角相等,则P点的轨迹是( )
A 椭圆 B 抛物线 C 圆 D 双曲线
8、某公司租地建仓库,每月士地占用费y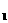 与仓库到车站的距离成反比,而每月库存货物费y
与仓库到车站的距离成反比,而每月库存货物费y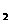 与到车站的距离成正比,如果在距离车站10公里处建仓库,这这两项费用y
与到车站的距离成正比,如果在距离车站10公里处建仓库,这这两项费用y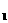 和y
和y 分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站
分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站
A 5公里处 B 4公里处 C 3公里处 D 2公里处
7、在 所在的平面上有一点
所在的平面上有一点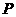 ,满足
,满足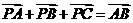 ,则
,则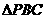 与
与 的面积之比是
的面积之比是
A.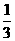 B.
B.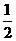 C.
C.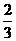 D.
D.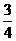
6、在等差数列中,若是a2+4a7+a12=96,则2a3+a15等于
A. 96 B. 48 C. 24 D. 12
5、已知椭圆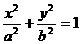
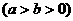 ,直线
,直线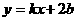 与椭圆交于不同的两点A、B,设
与椭圆交于不同的两点A、B,设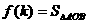 ,则函数
,则函数 为( )
为( )
A 奇函数 B 偶函数 C 既不是奇函数又不是偶函数 D 无法判断
4、若复数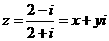 ,x,y
,x,y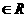 ,则
,则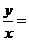 ( )
( )
A. 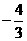 B.
B.
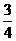 C.
C.
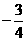 D.
D.
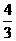
3、若函数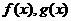 的定义域都是R,则
的定义域都是R,则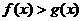 ,x∈R的充要条件是( )
,x∈R的充要条件是( )
A. 有一个x∈R,使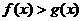 B. 有无数多个x∈R,使
B. 有无数多个x∈R,使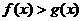
C. 对任意的x∈R,使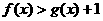 D. 不存在x∈R使
D. 不存在x∈R使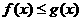
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com