
题目列表(包括答案和解析)
11、输入x=5,运行下面的程序之后得到y等于_____。
Input x
If x<0 then 
y=(x+1)*(x+1) 
Else 
y=(x-1)*(x-1) 
End
if
Print y
End
(二)选做题(14、15题考生只能从中选作一题, 如果两题都做,按第一题得分给分)
14. (坐标系与参数方程选做题)在极坐标系中,直线
(坐标系与参数方程选做题)在极坐标系中,直线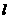 的方程为
的方程为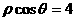 , 则点
, 则点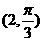 到直线
到直线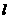 的距离为 _________ .
的距离为 _________ .
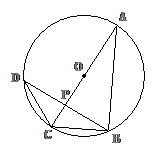
15. (几何证明选讲选做题)如图,  为⊙O的直径,弦
为⊙O的直径,弦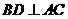 于点
于点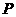 ,
,
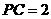 ,
,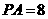 ,则
,则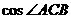 的值为 __________.
的值为 __________.
16、已知函数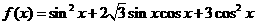 .
.
(Ⅰ)求函数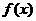 的最小正周期;
的最小正周期;
(Ⅱ)已知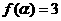 ,且
,且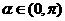 ,求
,求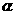 的值.
的值.
广东省崇雅中学2011届文科数学基础训练10
一 选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合要求的。 
1、设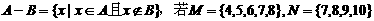 ,则M-N等于
,则M-N等于
A.{4,5,6,7,8,9,10} B.{7,8}
C.{4,5,6,9,10} D.{4,5,6} 
2、不等式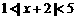 的解集是
的解集是

A.(-1,3) B.(-3,1)∪(3,7)
C.(-7,-3) D.(-7,-3)∪(-1,3)
3、已知向量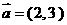 ,
,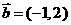 ,若
,若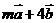 与
与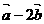 共线,则
共线,则 的值为
的值为
A 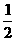 B
B
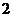 C
C
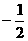 D
D 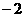

4、定义域为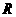 的奇函数
的奇函数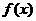

A 没有零点 B 有且只有一个零点 C 至少一个零点 D 至多一个零点
5、设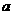 是甲抛掷一枚骰子得到的点数。则方程
是甲抛掷一枚骰子得到的点数。则方程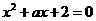 有两个不相等的实数根的概率为
有两个不相等的实数根的概率为
A 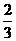 B
B 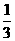 C
C 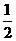 D
D 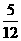

6、已知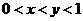 ,
,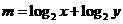 ,则有
,则有

A 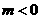 B
B 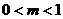 C
C 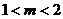 D
D 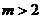

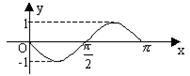 7、已知函数
7、已知函数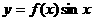 的一部分图象如右图所示,则函数
的一部分图象如右图所示,则函数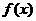 可以是
可以是
A 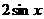 B
B 


C 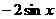 D
D 

8、使不等式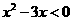 成立的必要不充分条件是
成立的必要不充分条件是
A 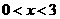 B
B 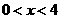 C
C 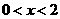 D
D
 ,或
,或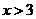

9、设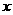 、
、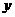 、
、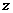 是空间不同的直线或平面,对下列四种情形:①
是空间不同的直线或平面,对下列四种情形:① 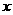 、
、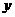 、
、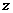 均为直线;
均为直线;
② 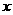 、
、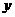 是直线,
是直线,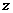 是平面;③
是平面;③ 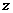 是直线,
是直线,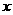 、
、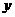 是平面;④
是平面;④ 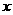 、
、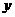 、
、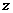 均为平面。
均为平面。
其中使“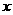 ⊥
⊥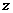 且
且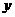 ⊥
⊥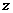
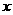 ∥
∥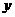 ”为真命题的是
”为真命题的是 
A ③ ④
B ① ③ C
② ③ D
① ②
10、已知点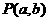
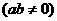 是圆
是圆 :
: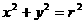 内一点,直线
内一点,直线 是以
是以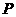 为中点的弦所在的直线,若直线
为中点的弦所在的直线,若直线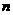 的方程为
的方程为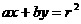 ,则
,则
A  ∥
∥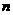 且
且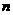 与圆
与圆 相离
B
相离
B  ∥
∥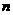 且
且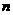 与圆
与圆 相交
相交
C  与
与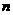 重合且
重合且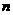 与圆
与圆 相离
D
相离
D  ⊥
⊥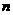 且
且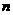 与圆
与圆 相离
相离
(一)必做题(11~13题)
11.已知椭圆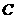 的中心在坐标原点,椭圆的两个焦点分别为
的中心在坐标原点,椭圆的两个焦点分别为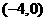 和
和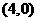 ,
,
且经过点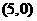 ,则该椭圆的方程为___________________
,则该椭圆的方程为___________________
12.设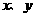 满足条件
满足条件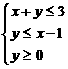 ,则点
,则点 构成的平面区域面积为________.
构成的平面区域面积为________.
13. 设定义在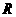 上的函数
上的函数 ,若关于
,若关于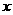 的方程
的方程
 有且只有3个不同实数解
有且只有3个不同实数解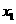 、
、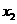 、
、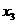 ,且
,且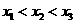 ,则
,则 ______
______
1.已知集合 ,则
,则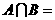 (
)
(
)
A.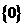 B.
B.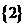 C.
C.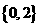 D.
D.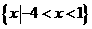
2.若复数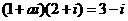 ,则实数
,则实数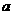 的值为
(
)
的值为
(
)
A.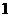 B.
B.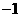 C.
C.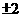 D.
D.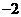
3.命题“ ,
,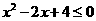 ”的否定为 ( )
”的否定为 ( )
A. ,
,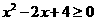 B.
B.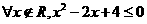
C.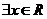 ,
,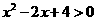 D.
D.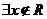 ,
,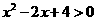
4.已知等差数列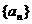 中,
中,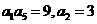 ,则
,则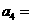 ( )
( )
A.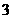 B.
B. C.
C.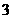 或
或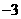 D.
D.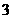 或
或
5.同时满足两个条件:①定义域内是减函数 ②定义域内是奇函数的函数是 ( )
A .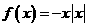 B.
B.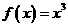 C.
C.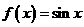 D.
D.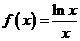
6.设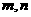 是两条不同的直线,
是两条不同的直线, 是两个不重合的平面,给定下列四个命题,其中为真命题的是
是两个不重合的平面,给定下列四个命题,其中为真命题的是
( )
 ①
① 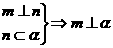 ②
② 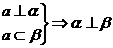
③ 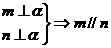 ④
④ 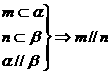
A. ①和② B. ②和③ C. ③和④ D. ①和④
7.如上图,在平行四边形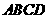 中,
中, 是对角线
是对角线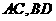 的交点,
的交点, 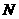 是线段
是线段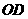 的中点,
的中点,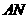 的延长线与
的延长线与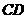 交于点
交于点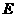 ,则下列说法错误的是
( )
,则下列说法错误的是
( )
A.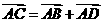 B.
B.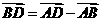 C.
C.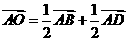 D.
D.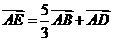
8.在平面直角坐标系 中,已知
中,已知 的顶点
的顶点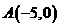 和
和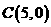 ,顶点
,顶点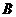 在双曲线
在双曲线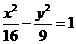 上,则
上,则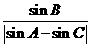 为
( )
为
( )
A. 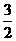 B.
B.
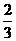 C.
C.
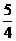 D.
D.
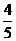
9.对于使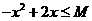 成立的所有常数
成立的所有常数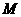 中,我们把
中,我们把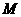 的最小值1叫做
的最小值1叫做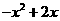 的“上确界”,若
的“上确界”,若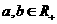 ,且
,且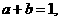 则
则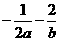 的“上确界”为
(
)
的“上确界”为
(
)
A. 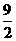 B.
B.
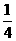 C.
C.
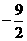 D.
D.
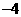
10.将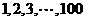 这
这 个自然数任意分成
个自然数任意分成 组,每组两个数,现将每组的两个数中任意一个记为
组,每组两个数,现将每组的两个数中任意一个记为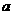 ,另一个数记为
,另一个数记为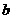 ,按框图所示进行运算(注:框图中每次“输入
,按框图所示进行运算(注:框图中每次“输入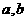 ”为同一组的
”为同一组的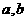 值,且每组数据不重复输入),则输出的
值,且每组数据不重复输入),则输出的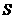 最大值为 (
)
最大值为 (
)
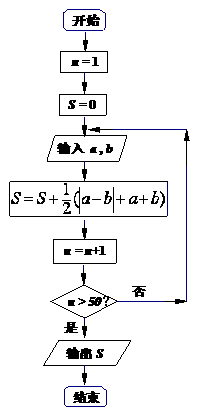 A.
A. B.
B.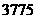 C.
C.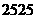 D.
D.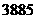
二。填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
16、(12分)假如关于某设备的使用年限x(年)和所支出的维修费y(万元),有如下统计资料:
|
使用年限x年 |
2 |
3 |
4 |
5 |
6 |
|
维修费用y万元 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料知y对x呈线性相关关系。
(1)求线性回归方程;
(2)估计使用年限为10年时,维修费用是多少?
参考公式:
用最小二乘法求线性回归方程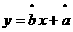 系数公式
系数公式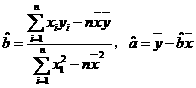 .
.
广东省崇雅中学2011届文科数学基础训练09
15、己知△ABC中,AB=AC,若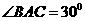 ,△ABC中BC边上的高
,△ABC中BC边上的高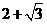 ,
,
则△ABC外接圆的面积____________。
三 解答题
14、已知曲线C的参数方程为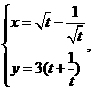 (
(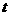 为参数,
为参数,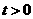 ),则曲线C的普通方程______________。
),则曲线C的普通方程______________。
13、函数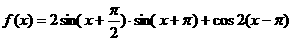 ,有下列命题:①周期
,有下列命题:①周期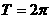 ;②其图象可以由
;②其图象可以由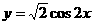 的图象向左平移
的图象向左平移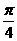 而得;③在区间[0,
而得;③在区间[0,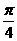 ]上单调递减;④其图象关于(
]上单调递减;④其图象关于(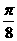 ,0)对称。其中正确的有______________(请把正确命题的序号都填上)
,0)对称。其中正确的有______________(请把正确命题的序号都填上)
12、右边的程序框图,输出的T= .
11、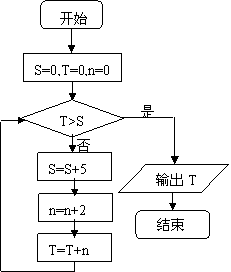 设变量x,y满足约束条件:
设变量x,y满足约束条件: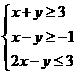 ,则
,则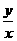 的
的
取值范围为________;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com