11. 打鼾不仅影响别人休息，而且可能与患某种疾病有关．下表是一次调查所得的数据，试问：每一晚打鼾与患心脏病有关吗？

10．以下是某地区不同身高的未成年男性的体重平均值表

(1)给出两个回归方程：①y＝0.4294x－25.318，②y＝2.004e^0.0197x通过计算，得到它们的相关指数分别是：R＝0.9311，R＝0.998.试问哪个回归方程拟合效果好？

(2)若体重超过相同身高男性平均值的1.2倍为偏胖，低于0.8为偏瘦，那么该地区某中学一男生身高为175 cm,78 kg，他的体重是否正常？

9．(2008年惠州一模)对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪研究，调查他们是否又发作过心脏病，调查结果如下表所示：

试根据上述数据计算K²＝________，比较这两种手术对病人又发作心脏病的影响有没有差别．________.

8．如果发现散点图中所有的样本点都在一条直线上，则残差平方和等于_________．解释变量和预报变量之间的相关系数等于__________．

7．关于x与y，有如下数据

有如下的两个模型：(1)＝6.5x+17.5，(2)＝7x+17.通过残差分析发现第(1)个线性模型比第(2)个拟合效果好．则R________R，Q₁______Q₂.

(用大于，小于号填空，R²，Q分别是相关指数和残差平方和)

6．若由一个2×2列联表中的数据计算得K²＝4.395，那么确认两个变量有关系的把握性有(　)

A．90% 　　B．95%　 　C．99% 　　D．99.5%

5. 独立性检验中的“小概率事件”是指某事件发生的概率 (　)

A．小于4% 　　B．小于5%　 　C．小于6% 　　D．小于8%

4．通过残差图我们发现在采集样本点过程中，第____个样本点数据不准确(　)

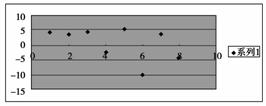
A．第四个　B．第五个　C．第六个　D．第八个

3．两个变量y与x的回归模型中，分别选择了4个不同模型，它们的相关指数R²如下 ，其中拟合效果最好的模型是(　)

A．模型1的相关指数R²为0.98

B．模型2的相关指数R²为0.80

C．模型3的相关指数R²为0.50

D．模型4的相关指数R²为0.25

2．设两个变量x和y之间具有线性相关关系，它们的相关系数为r，y关于x的回归直线方程为＝kx+b，则(　)

A．b与r的符号相同　　 　B．k与r的符号相同

C．b与r的符号相反 　　　　D．k与r的符号相反