
题目列表(包括答案和解析)
2.球的表面积公式: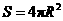 (
(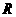 为球的半径).
为球的半径).
1.球的体积公式: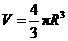 (
(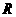 为球的半径).
为球的半径).
3.台体的体积公式: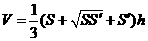 (
(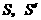 分别为上下底面面积,
分别为上下底面面积,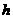 为高).
为高).
圆台的体积公式也可以表示为: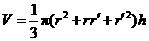 (
(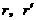 分别为上下底面半径,
分别为上下底面半径,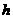 为高).
为高).
③ 柱体、锥体、台体的体积公式之间的关系
柱体 台体 锥体
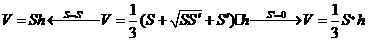
④ 思路点拨
将一些不规则的几何体进行修补或者将一些组合体进行分割,转化成一些规则的几何体,是求体积的一种重要思想方法.例如,常见的将三棱柱补成四棱柱,四棱锥分割成三棱锥,再利用四棱柱、三棱锥的特殊性求体积,是经常用的割补形式.
2.锥体的体积公式: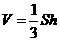 (
(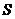 为底面面积,
为底面面积,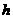 为高).圆锥的体积公式也可以表示为:
为高).圆锥的体积公式也可以表示为:
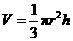 (
( 为底面半径,
为底面半径,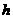 为高).
为高).
1.柱体的体积公式: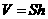 (
(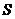 为底面面积,
为底面面积,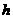 为高).圆柱的体积公式也可以表示为:
为高).圆柱的体积公式也可以表示为:
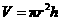 (
( 为底面半径,
为底面半径,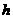 为高).
为高).
4. 思路点拨
(1)在解题过程中,应注意分清要求的是底面积还是表面积.
(2)将空间图形问题转化为平面图形问题,是立体几何中最基本的,也是最常用的方法.
3. 圆柱、圆锥、圆台的表面积公式间的转化
圆柱 圆台 圆锥
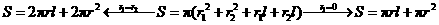
2. 圆柱、圆锥、圆台的表面积
(1) 圆柱
① 圆柱的侧面展开图是一个矩形
②
如果圆柱的底面半径为 ,母线长为
,母线长为 ,则圆柱的表面积为
,则圆柱的表面积为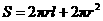 .
.
(2) 圆锥
① 圆锥的侧面展开图是一个扇形.
②
如果圆锥的底面半径为 ,母线长为
,母线长为 ,则圆锥的表面积为
,则圆锥的表面积为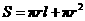 .
.
(3) 圆台
① 圆台的侧面展开图是一个扇环.
②
如果圆台的上、下底面半径为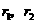 ,母线长为
,母线长为 ,
,
则圆台的表面积为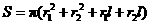 .
.
1. 棱柱、棱锥、棱台表面积的计算
棱柱,棱柱,棱台是由若干个平面图形围成的几何体,它们的表面积就是各表面的面积之和.我们可以把它们展开成一个平面图形,利用平面图形求面积的方法,求得它们的表面积.
2.忽视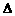 法求值域须对两个端点值进行检验.
法求值域须对两个端点值进行检验.
正解:方法一:原式可化为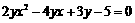 .(※)
.(※)
当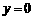 时,(※)式显然不成立.
时,(※)式显然不成立.
当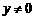 时,
时,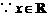 ,
,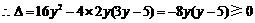 ,
,
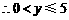 ,
,
当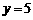 时,由(※)式得
时,由(※)式得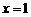 显然适合定义域(定义域为R),
显然适合定义域(定义域为R),
从而所求函数的值域为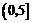
方法二: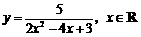 ,
,
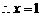 时,
时,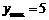 ,当
,当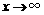 时,
时,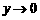 .
.
故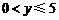 ,从而所求函数的值域为
,从而所求函数的值域为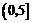 .
.
建立并用好纠错本能从反面入手,深刻理解和掌握基本概念基本方法和基本技巧,能针对自己的不足对症下药,如果自己每次出现的错误都能及时得到纠正,长期坚持下去,就可以逐步摆脱学习困境.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com