
题目列表(包括答案和解析)
例3 若 ,则有( )
,则有( )
A.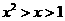 B.
B.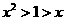 C.
C.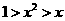 D.
D.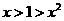
解:设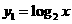 ,
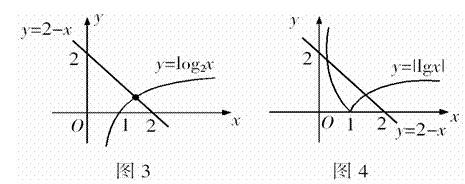
,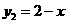 ,在同一坐标系中作出其简图,如图3.
,在同一坐标系中作出其简图,如图3.
由图3知,交点的横坐标 ,则有
,则有 .
.
 选 A.
选 A.
例2 已知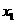 是方程
是方程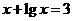 的根,
的根,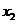 是方程
是方程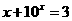 的根,那么
的根,那么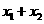 的值为( )
的值为( )
A.6 B.3 C.2 D.1
解: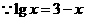 ,
,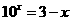 ,令
,令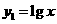 ,
,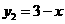 ,
,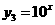 ,在同一坐标系中作出它们的简图,如图2.
,在同一坐标系中作出它们的简图,如图2.
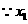 是方程
是方程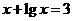 的解,
的解,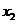 是方程
是方程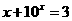 的解,
的解,
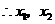 分别对应图中
分别对应图中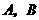 两点的横坐标.
两点的横坐标.
 函数
函数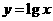 与
与 的图象关于
的图象关于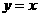 对称,
对称,
 线段
线段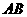 的中点
的中点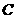 在直线
在直线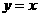 上.
上.
 由
由 解得
解得 .
.
 ,故选 B.
,故选 B.
例1 已知函数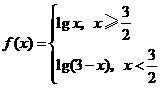 ,若方程
,若方程 无实数根,则实数
无实数根,则实数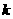 的取值范围是( )
的取值范围是( )
A.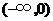 B.
B. C.
C.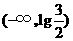 D.
D.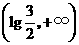
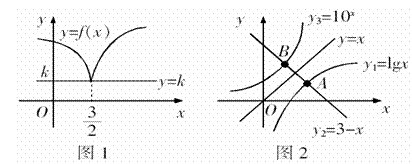
分析:所给的函数 是分段函数,而方程
是分段函数,而方程 无实数根,可利用数形结合法转化为两函数图象无交点.
无实数根,可利用数形结合法转化为两函数图象无交点.
解:在同一坐标系内作出函数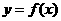 与
与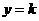 的图象,如图1,
的图象,如图1,
 若两函数图象无交点,则
若两函数图象无交点,则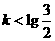 ,故选 C.
,故选 C.
如果已知函数解析式的结构时,常用待定系数法求 ( x)的解析式,其解题基本思路是:先设出
( x)的解析式,其解题基本思路是:先设出 ( x)的一般表达式,再根据已知条件确定出表达式中的参数即得
( x)的一般表达式,再根据已知条件确定出表达式中的参数即得 ( x)的解析式.
( x)的解析式.
例4 设 (x)是x的二次函数,g(x) = 2
(x)是x的二次函数,g(x) = 2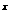 ·
· (x),且g(x + 1)-g(x) = 2
(x),且g(x + 1)-g(x) = 2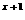 ·x
·x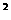 ,求函数
,求函数 (x)和g(x)的解析式.
(x)和g(x)的解析式.
解:设 (x) = ax
(x) = ax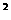 + bx + c (a≠0),则g(x) = 2
+ bx + c (a≠0),则g(x) = 2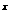 ·(ax
·(ax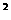 + bx + c).
+ bx + c).
由g(x + 1)-g(x) = 2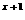 ·x
·x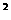 得:
得:
2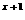 ·[a (x + 1)
·[a (x + 1)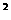 + b(x + 1) + c]-2
+ b(x + 1) + c]-2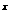 ·(ax
·(ax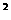 + bx + c) = 2
+ bx + c) = 2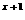 ·x
·x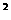 ,
,
即ax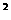 + (4a + b)x + (2a + 2b + c) = 2x
+ (4a + b)x + (2a + 2b + c) = 2x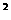 .这是关于x的恒等式,比较系数,得
.这是关于x的恒等式,比较系数,得



∴ (x) = 2x
(x) = 2x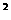 -8x + 12 ,g(x) = 2
-8x + 12 ,g(x) = 2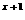 ·(x
·(x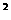 -4x + 6).
-4x + 6).
通过赋予不同变量构造一组方程,通过解新旧方程的方法求出 (x)的解析式.
(x)的解析式.
例3 设 (x)满足2x
(x)满足2x (x)-3
(x)-3 (
(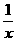 ) = x
) = x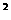 + 1 ①,求函数
+ 1 ①,求函数 (x) 的解析式.
(x) 的解析式.
解:用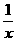 替换①式中的x,得2
替换①式中的x,得2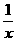
 (
(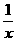 )-3
)-3 (x) =
(x) =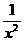 + 1,即2
+ 1,即2 (
(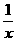 )-3x
)-3x (x) =
(x) =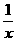 + x ②,
+ x ②,
①、②两个方程联立,消去 (
(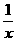 )得:
)得: (x) =-
(x) =-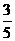 -
-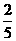 x-
x-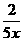 -
-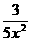 .
.
当所给函数含有两个不同的变量时,常用特殊值代入法求 (x)的解析式,其解题基本思路是:令变量取某些特殊值,从而减少未知元,求出
(x)的解析式,其解题基本思路是:令变量取某些特殊值,从而减少未知元,求出 (x)的解析式.
(x)的解析式.
例2 已知 (x)是定义在R上的函数,且
(x)是定义在R上的函数,且 (0) = 1,
(0) = 1, ( y-x) =
( y-x) = (y)-xe
(y)-xe ,求函数
,求函数 (x)的解析式.
(x)的解析式.
解:取x = y,则由已知等式,有 (0) =
(0) = (x)-xe
(x)-xe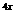 ,
,
∵ (0) = 1,∴
(0) = 1,∴ (x) = 1 + xe
(x) = 1 + xe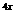 .
.
如果已知复合函数 [g(x)]的表达式时,常用换元法求出函数
[g(x)]的表达式时,常用换元法求出函数 (x)的解析式.其解题基本思路是:先令g(x) = t,从中求出x,再代入
(x)的解析式.其解题基本思路是:先令g(x) = t,从中求出x,再代入 [g(x)]中即得
[g(x)]中即得 ( x)的解析式.
( x)的解析式.
例1
已知 (x +
(x +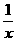 ) = x
) = x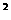 +
+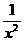 ,求函数
,求函数 (x)的解析式.
(x)的解析式.
解:t = x +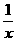 ,又x
,又x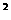 +
+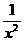 = (x +
= (x +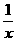 )
)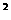 -2,且| x +
-2,且| x +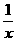 |≥2,即| t |≥2.
|≥2,即| t |≥2.
∴ ( t) = t
( t) = t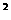 -2
(| t |≥2),即
-2
(| t |≥2),即 ( x) = x
( x) = x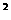 -2
(| x |≥2).
-2
(| x |≥2).
评注:在用换元法解题时,一定要注意定义域的变化,注意前边的x与后边的x的区别与联系.所求的函数关系要注明定义域.
例5 如果直线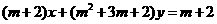 与
与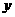 轴平行,求
轴平行,求 的值.
的值.
误: 直线与
直线与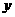 轴平行,
轴平行,
 .
.
解得 或
或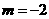 .
.
所以当 或
或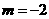 时直线与
时直线与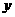 轴平行.
轴平行.
析:由于方程 表示直线,本身隐含着
表示直线,本身隐含着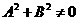 这一条件.当
这一条件.当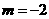 时,直线方程
时,直线方程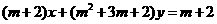 为
为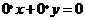 ,它不表示直线,应舍去.
,它不表示直线,应舍去.
故当 时直线与
时直线与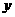 轴平行.
轴平行.
例4
直线 经过点
经过点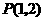 ,且点
,且点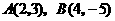 到
到 的距离相等,求直线
的距离相等,求直线 的方程.
的方程.
误:因为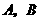 两点到直线
两点到直线 的距离相等,所以
的距离相等,所以 .
.
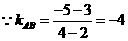 ,
,
 由点斜式可得所求直线方程为
由点斜式可得所求直线方程为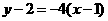 ,即
,即 .
.
析:由于两点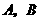 到直线
到直线 的距离相等,故应有点
的距离相等,故应有点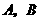 在直线的同侧或异侧两种情况,而本题只考虑了
在直线的同侧或异侧两种情况,而本题只考虑了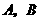 两点在直线的同侧,忽视了两点在直线的异侧的情况,从而导致错误.因此,应有当
两点在直线的同侧,忽视了两点在直线的异侧的情况,从而导致错误.因此,应有当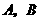 两点在直线的异侧时,直线
两点在直线的异侧时,直线 经过
经过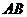 的中点
的中点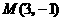 .所以由两点式得所求直线方程为
.所以由两点式得所求直线方程为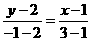 ,即
,即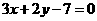 .
.
故所求直线方程为 或
或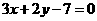 .
.
例3
求过点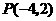 且与
且与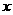 轴的交点到
轴的交点到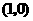 的距离为5的直线方程.
的距离为5的直线方程.
误:设直线的斜率为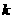 ,则其方程为
,则其方程为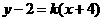 .
.
则其与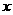 轴的交点为
轴的交点为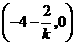 .
.
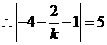 ,解得
,解得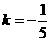 .
.
故所求直线方程为 .
.
析:本题由于只注意了直线的斜率存在的情况而忽视了直线的斜率不存在的情况,即过点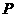 且垂直于
且垂直于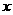 轴的直线而导致错误.其实直线
轴的直线而导致错误.其实直线 也适合题意.故所求直线方程为
也适合题意.故所求直线方程为 或
或 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com