
题目列表(包括答案和解析)
6. 已知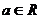 ,函数
,函数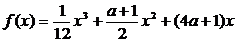 .
.
(1)如果函数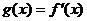 是偶函数,求
是偶函数,求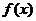 的极大值和极小值;
的极大值和极小值;
(2)如果函数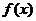 是
是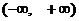 上的单调函数,求
上的单调函数,求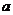 的取值范围.
的取值范围.
|
批阅时间 |
等级 |
|
|
|
姓名 作业时间: 2010 年 月 日 星期 作业编号 031
5. 已知函数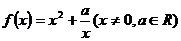
(1)判断函数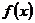 的奇偶性;
的奇偶性;
(2)若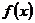 在区间
在区间 是增函数,求实数
是增函数,求实数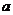 的取值范围。
的取值范围。
4. 汽车在匀速行驶过程中,汽油平均消耗率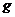 (即每小时的汽油耗油量,单位:
(即每小时的汽油耗油量,单位: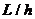 )与汽车行驶的平均速度
)与汽车行驶的平均速度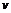 (单位:
(单位: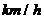 )之间满足:
)之间满足: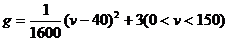 ,若定义“汽油的使用率最高”为每千米汽油平均消耗量最少(单位:
,若定义“汽油的使用率最高”为每千米汽油平均消耗量最少(单位: ),则汽油的使用率最高时,汽车速度是
),则汽油的使用率最高时,汽车速度是 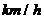 。
。
3. 若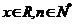 ,规定:
,规定: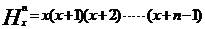 ,例如:
,例如: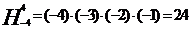 ,则
,则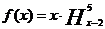 的奇偶性为
。
的奇偶性为
。
2. 若函数 在
在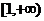 上的最大值是
上的最大值是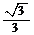 ,则实数
,则实数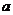 的取值范围是
.
的取值范围是
.
1. 若函数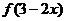 的定义域为[-1,2],则函数
的定义域为[-1,2],则函数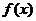 的定义域是
。
的定义域是
。
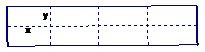
4.如图所示是某水产养殖场的养殖大网箱的平面图,四周的实线为网衣,为避免混养,用筛网(图中虚线)把大网箱隔成大小一样的小网箱。
(1)若大网箱的面积为108平方米,每个小网箱的长x,宽y设计为多少米时,才能使围成的网箱中筛网总长度最小;
(2)若大网箱的面积为160平方米,网衣的造价为112元/米,筛网的造价为96元/米,且大网箱的长与宽都不超过15米,则小网箱的长、宽为多少米量,可使总造价最低?
|
批阅时间 |
等级 |
|
|
|
姓名 作业时间: 2010 年 月 日 星期 作业编号 030
3.已知等差数列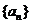 满足:
满足: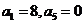 。数列
。数列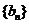 的前n项和为
的前n项和为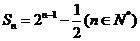
(1)求数列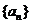 和
和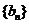 的通项公式;
的通项公式;
(2)令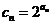 ,试问:是否存在正整数n,使不等式
,试问:是否存在正整数n,使不等式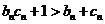 成立?若存在,求出相应n的值;若不存在,请说明理由。
成立?若存在,求出相应n的值;若不存在,请说明理由。
2.如图,函数 的图象在点P处的切线是
的图象在点P处的切线是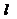 ,则
,则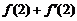 =
.
=
.
1. 已知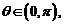 函数
函数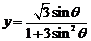 的最大值____________。
的最大值____________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com