
题目列表(包括答案和解析)
7.对异面直线的概念要着重明确如下几点:
(1)两条直线若异面则必不能同在任何一个平面内,因此它们不相交也不平行.
(2)分别在某两个平面内的两条直线,不一定是异面直线,如图3.
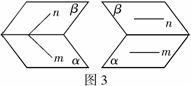
(3)画异面直线时,以辅助平面作衬托,更为直观,如图4.
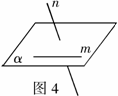
6.立体几何中,被遮住的部分可画成虚线或不画,为了不产生混淆,立体图形的直观图中,辅助线和图形中原有的线同样处理,可见部分不画成虚线.
5.立体几何中,通常画平行四边形表示平面,但应注意以下几点:
(1)所画的平行四边形是表示它所在的整个平面,需要时我们可以把它扩展出去,这同画直线一样,直线是可以无限延伸的,但在画图时也只能画一段来表示直线.
(2)加“通常”两字的意思,是因为有时根据需要也可用其他的平面图形,如菱形、封闭的曲线图形等来表示平面.
(3)画表示水平平面的平行四边形时,通常把它的锐角画成45°,横边画成邻边的两倍,也可根据图形的不同需要来画,并不强求一律.画相交平画时,一定要画出它们的交线.
4.注意与平面几何的比较
对平面图形的研究是讨论立体图形的基础;立体图形的问题常常转化为平面图形的问题来解决.将立体几何与平面几何的“同类问题”进行比较学习有助于我们学好立体几何.例如,在平面几何中,两直线的位置关系只有两种,但在立体几何中两直线的位置关系却有三种;四边相等的四边形在平面几何中的图形是菱形,但在立体几何中的图形是菱形或空间四边形.
3.注意空间点、线、面之间位置关系的自主探究
学习本节课前,请同学们准备好一个长方体的几何模型.现在拿出你的长方体几何模型,再拿出一支铅笔(权当直线)或一本书(权当平面),通过比划你会很快得出直线与直线、直线与平面、平面与平面的位置关系.
2.注意数学语言和图形语言的复习
数学语言我们并不陌生,在集合中我们学习过很多.学好立体几何的数学语言,能使立体几何语言的表达方法简明扼要、清楚明白、符合逻辑;在这里提醒同学们注意:①点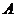 在立体几何中永远是元素,直线
在立体几何中永远是元素,直线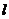 和平面
和平面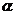 均是集合,因此,有
均是集合,因此,有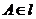 ,
,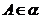 ,
,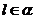 或
或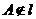 ,
,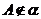 ,
,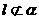 ;②直线
;②直线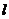 与平面
与平面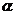 相交记作
相交记作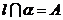 ,它是
,它是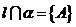 的简记并没错误.
的简记并没错误.
图形语言的学习就是如何快速准确地作出空间图形的学习.空间图形是画在一个平面内的,因此识图和画图的技巧就十分重要.如何根据题目的条件画出图形,需要用实物模型参考,更需要多观察、多比较、多分析,逐步积累一些画法技巧,同时要注意图形的合理性、美观性和直观性.有些性质的判定和长度的计算及点的位置的确定,往往借助图形就可以估算一个大概,这有利于最后经过计算或论证得到结果的验证.
1.注意公理的复习
公理是人们经过长期观察与实践总结出来的,因此我们在学习公理时,要对图形进行认真的观察并动手进行验证;同时公理是几何推理的基本依据,也是我们进一步学习和研究空间图形的基础,所以我们不但要熟记公理的内容,还要知道每个公理的用途和如何用.例如,公理1是用来判断直线是否在平面内的依据,如果要判断一直线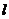 在平面
在平面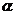 内,就要想办法在直线l上找出不重合的两点
内,就要想办法在直线l上找出不重合的两点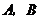 ,证明
,证明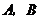 两点均在平面
两点均在平面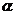 内.
内.
在这里提醒同学们注意,公理3是确定一个平面的依据,我们对公理3进一步探究发现,“两条相交直线可以确定一个平面”、“两条平行线可以确定一个平面”、“一条直线和直线外一点可以确定一个平面”这些推论都可以作为确定一个平面的依据,而且应用很广.
 例1 已知四边形
例1 已知四边形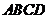 中,
中,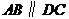 ,
,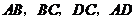 所在直线分别与平面
所在直线分别与平面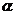 交于点
交于点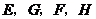 ,求证:
,求证: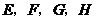 必共线.
必共线.
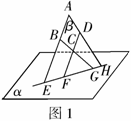
证明:如图1,∵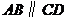 ,
,
∴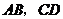 共面.
共面.
设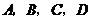 确定平面
确定平面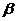 ,
,
∵点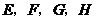 分别在直线
分别在直线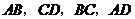 上,
上,
∴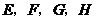 都在
都在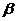 内,
内,
又∵点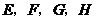 在平面
在平面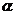 内,
内,
∴点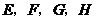 在
在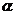 和
和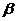 的交线上,即
的交线上,即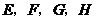 共线.
共线.
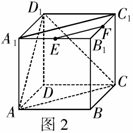 说明:要证明多点共线,只需证这些点同在两个相交平面的交线上,这是证点共线的常用方法之一,其理论依据是公理2.
说明:要证明多点共线,只需证这些点同在两个相交平面的交线上,这是证点共线的常用方法之一,其理论依据是公理2.
例2 已知:正方体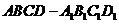 中,
中,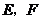 分别是棱
分别是棱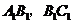 的中点,求异面直线
的中点,求异面直线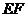 与
与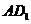 所成角的大小.
所成角的大小.
解:如图2,分别连结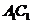 ,
,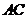 .
.
∵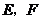 分别是
分别是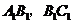 的中点,∴
的中点,∴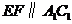 .
.
又∵在正方体中,
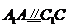 ,
,
∴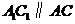 .∴
.∴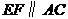 .
.
∴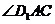 的大小即为所求,连结
的大小即为所求,连结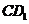 ,
,
∵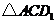 为正三角形,
为正三角形,
∴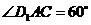 ,
,
故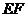 与
与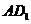 所成角为60°.
所成角为60°.
说明:求异面直线所成的角的问题,关键是抓住平移,将三维空间两直线所成的角的问题转化为二维平面两相交直线所成角问题来研究.
3.两条直线的位置关系
(1)两条直线的三种位置关系:
a.相交:共面,有且只有一个公共点.
b.平行:共面,没有公共点.
c.异面:不同在任何一个平面内,没有公共点.
(2)异面直线的判定方法:
a.定义:不同在任何一个平面内的两条直线,称为异面直线.
b.判定定理:若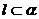 ,
,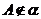 ,
,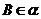 ,
,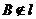 ,则直线
,则直线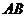 和
和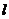 是异面直线.
是异面直线.
(3)公理4(平行公理)、等角定理及推论
公理4是论证平行问题的主要根据,也是确定平面的基础.等角定理及其推论是证明空间两角相等的重要理论依据.
(4)异面直线所成的角的概念及其取值范围
a.异面直线所成的角的定义中,异面直线a和b所成的角和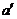 与
与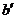 所成的锐角(或直角)相等,但与点
所成的锐角(或直角)相等,但与点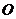 的位置无关,因此在解具体问题时,可将点
的位置无关,因此在解具体问题时,可将点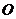 取在a或b上,或者取几何体中具有特殊性的点.
取在a或b上,或者取几何体中具有特殊性的点.
b.要明确过空间一点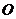 ,引直线a的平行线的方法和依据.因为
,引直线a的平行线的方法和依据.因为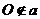 ,所以点O和a确定一个平面
,所以点O和a确定一个平面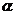 ,在面
,在面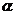 内过点
内过点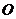 作
作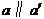 ,作
,作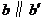 .
.
c.两条异面直线互相垂直,它们所成的角为90°,今后再说两条直线互相垂直,它们可能相交,也可能异面.
d.异面直线所成的角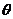 的范围是
的范围是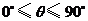
2.平面的基本性质
(1)“有且只有一个”的含义:
“有”说明图形是存在的,“只有一个”说明图形是唯一的.数学中的“只有一个”并不保证符合条件的图形一定存在,所以不能用“只有一个”来代替“有且只有一个”,符合某一条件的图形既存在,而且只能有一个,就说明这个图形完全是确定的,因此“有且只有一个”和“确定”是同义词.
(2)公理1是判定直线在平面内或点在平面内的工具.
例如: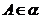 、
、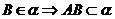 ,又如
,又如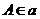 ,
,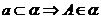 .
.
(3)公理2给出了确定两个相交平面的交线的方法.根据公理2要找到两个平面的交线,只要找出它们的两个公共点,经过这两点的直线就是它们的交线,同时公理2还可以用来证明点在直线上,即如果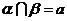 ,
,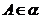 且
且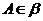 ,则
,则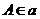 ,进而可证明三点共线.
,进而可证明三点共线.
(4)公理3及其推论是确定平面和判定平面重要的依据.
在立体几何中,常常需将空间图形问题转化为平面图形的问题,进而利用平面几何知识来求解,因此要确定诸元素是否在同一个平面内,而公理3及其推论正是起着确定平面的作用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com