
题目列表(包括答案和解析)
1.已知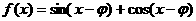 为奇函数,则
为奇函数,则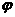 的一个取值
的一个取值
A.0
B.π C.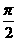 D.
D.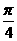
8. 已知集合A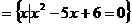 ,B
,B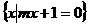 ,且
,且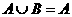 ,求实数
,求实数 的值组成的集合。
的值组成的集合。
7.若不等式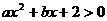 的解集为
的解集为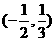 ,求
,求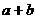 的值
的值
6. 设二次函数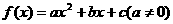 ,若
,若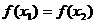 (其中
(其中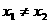 ),则
),则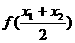 等于
_____.
等于
_____.
5. 已知全集U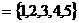 ,A
,A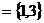 ,B
,B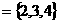 ,那么
,那么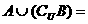 ___.
___.
4. 函数f(x)=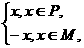 其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=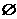 ,则f(P)∩f(M)=
,则f(P)∩f(M)=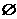 ; ②若P∩M≠
; ②若P∩M≠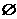 ,则f(P)∩f(M) ≠
,则f(P)∩f(M) ≠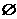 ;③若P∪M=R,则f(P)∪f(M)=R; ④若P∪M≠R,则f(P) ∪f(M)≠R.其中正确判断有
;③若P∪M=R,则f(P)∪f(M)=R; ④若P∪M≠R,则f(P) ∪f(M)≠R.其中正确判断有
A 0个 B 1个 C 2个 D 4个
3. 设命题甲: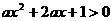 的解集是实数集R;命题乙:
的解集是实数集R;命题乙: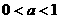 ,则命题甲是命题乙成立的
,则命题甲是命题乙成立的
A . 充分非必要条件 B.必要非充分条件
C. 充要条件 D. 既非充分又非必要条件
2.一元二次方程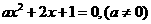 有一个正根和一个负根的充分不必要条件是:
有一个正根和一个负根的充分不必要条件是:
A.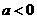 B.
B.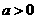 C.
C.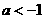 D.
D.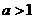
1. 若集合M={y| y=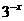 },P={y| y=
},P={y| y=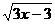 }, 则M∩P=
}, 则M∩P=
A{y| y>1} B{y| y≥1} C{y| y>0} D{y| y≥0}
例 用二分法求函数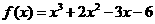 的一个正零点(精确到0.1).
的一个正零点(精确到0.1).
解析:由于要求的是函数的一个正零点,因此可以考虑首先确定一个包含正零点的恰当区间,如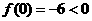 ,
,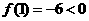 ,
,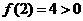 ,故可取区间
,故可取区间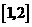 为计算的初始区间(当然
为计算的初始区间(当然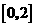 也可以),用二分法逐次计算,列表如下:
也可以),用二分法逐次计算,列表如下:
|
区间 |
中点 |
中点函数值 |
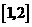 |
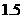 |
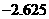 |
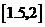 |
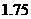 |
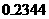 |
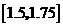 |
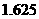 |
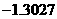 |
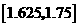 |
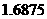 |
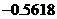 |
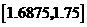 |
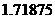 |
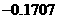 |
由上表计算可知,区间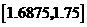 的长度
的长度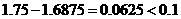 ,所以可以将
,所以可以将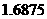 的近似值
的近似值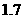 作为函数零点的近似值.
作为函数零点的近似值.
评注:在用二分法求函数零点时,若函数能因式分解,可先将其因式分解,进而求得零点,再依据零点确定一个包含零点的恰当区间.如本题可将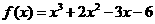 变形为
变形为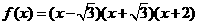 ,则函数零点为
,则函数零点为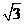 ,
,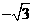 ,
,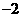 ,再根据
,再根据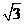 选取一个恰当区间.
选取一个恰当区间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com