
题目列表(包括答案和解析)
2.在画两个平面相交时,若一个平面被另一平面遮住,则被遮住的部分应画成虚线,或者不画,交线必须画出来,以突出立体感.
1.根据平面的基本性质 ,常将立体几何问题转化为平面几何问题解决.
| 空间的点和直线之间的位置关系有点在直线上和点不在直线上两种.
| 空间的点和平面之间的位置关系有点在平面内和点在平面外两种.
| 空间直线和直线之间的位置关系有相交,平行和异面三种.其中,当两条直线相交或者平行时,这两条直线是共面的.
若从公共点的数目方面看,可以分为:
(1)只有一个公共点--相交直线;
(2)没有公共点
若从平面的基本性质方面看,可以分为:
(1)在同一平面内
(2)不同在任一平面内--异面直线.
注:(1)在异面直线所成的角的定义中,点 是任意选取的,根据等角定理,可以肯定异面直线
是任意选取的,根据等角定理,可以肯定异面直线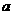 和
和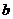 所成的角与
所成的角与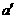 和
和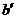 所成的锐角(或直角)相等,而和点
所成的锐角(或直角)相等,而和点 的位置无关.在这里,如果两条异面直线所成的角是直角时,则称这两条异面直线互相垂直.
的位置无关.在这里,如果两条异面直线所成的角是直角时,则称这两条异面直线互相垂直.
(2)异面直线所成的角的取值范围为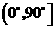 .
.
| 空间直线和平面之间的位置关系有直线在平面内,直线和平面相交, 直线和平面平行三种.其中, 直线和平面相交或者直线和平面平行时,又称为直线在平面外.
| 平面和平面之间的位置关系有相交和平行两种.
u 公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
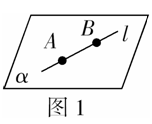 (1)图形语言描述为:如图1.
(1)图形语言描述为:如图1.
(2)符号语言表述为:若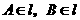 ,且
,且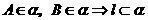 .
.
(3)作用:一是可以用来判定一条直线是否在平面内,即要判定直线在平面内,只需确定直线上有两个点在平面内即可;二是可以用来判定点在平面内,即如果直线在平面内、点在直线上,则点在平面内.
u 公理2:过不在一条直线上的三点,有且只有一个平面.
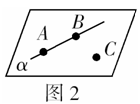 (1)图形语言描述为:如图2.
(1)图形语言描述为:如图2.
(2)符号语言表述为: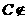 直线
直线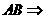 存在惟一的平面
存在惟一的平面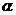 ,使得
,使得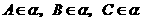 .
.
(3)作用:确定平面的依据,判定两平面重合的依据.
u
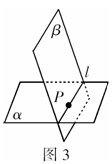 公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
(1)图形语言描述为:如图3.
(2)符号语言表述为: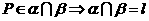 ,且
,且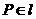 .
.
(3)作用:一是判定两个平面相交,即如果两个平面有一个公共点,那么这两个平面相交;二是判定点在直线上,即点若是某两个平面的公共点,那么这点就在这两个平面的交线上;三是判定三点共线;四是确定交线位置的依据.
u 公理4:平行于同一条直线的两条直线平行.
(1)符号语言表述为:若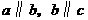 ,则
,则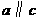 .
.
(2)作用:该公理是判断两条直线平行的一种方法.
等角定理的条件有两个:一是一个角的两边与另一个角的两边分别平行;二是一个角的两边与另一个角的两边方向相同.只有同时满足这两个条件,这两个角才相等.
l 平面及其性质 平面是一个不加定义,只需理解的最基本的原始概念.与生活中常见的平面相比较,我们所学的立体几何中的平面是一个理想化的模型,它具有无限延展的性质,既没有大小之说,也没有厚薄之分.
l 平面的画法 立体几何中常常用一个锐角为45°的平行四边形来表示一个平面,有时根据需要也可用三角形、矩形、圆等平面图形来表示一个平面.
l
平面的表示方法 平面通常用小写的希腊字母来表示,如平面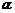 ,
,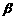 ,
,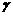 等,也可用代表平行四边形的四个顶点,或者相对的两个顶点的大写字母来表示,如平面ABCD,平面BD等.
等,也可用代表平行四边形的四个顶点,或者相对的两个顶点的大写字母来表示,如平面ABCD,平面BD等.
5.证明线与线、线与面的平行关系的一般思考规律是:“见了已知想性质,见了求证想判定”,也就是“发展已知,转化结论,沟通已知与未知的关系”,这是分析问题和解决问题的一般思维方法.而作辅助线和辅助面往往是沟通已知和未知的有效手段.
4.证明线线平行、线面平行一般用直接证法.证明直线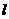 与平面
与平面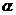 平行,通常有以下两个途径:①通过线线平行来证明,即证明该直线
平行,通常有以下两个途径:①通过线线平行来证明,即证明该直线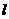 平行于平面
平行于平面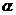 内的一条直线;②通过面面平行来证明,即证明过该直线
内的一条直线;②通过面面平行来证明,即证明过该直线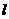 的一个平面平行于平面
的一个平面平行于平面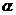 .
.
3.直线与平面平行的判定定理及性质定理的实质就是线线平行与线面平行的转化.性质定理将空间线面平行关系转化为平面内线线平行关系(降维转化),判定定理正好与此相反,体现了平面与空间的对立统一关系.要学会用转化思想处理立体几何问题,要认真领会和掌握线线、线面、面面平行的相互转化关系.即:线线平行 线面平行
线面平行 面面平行.因此,要判断某一平行的过程就是从一平行出发不断转化的过程.在解题时要把握这一点,灵活确定转化思路和方向.
面面平行.因此,要判断某一平行的过程就是从一平行出发不断转化的过程.在解题时要把握这一点,灵活确定转化思路和方向.
2.两个平面平行问题的判定或证明,是将其转化为一个平面内的直线与另一个平面平行的问题,即“线面平行,则面面平行”.必须注意这里的“线面”是指一个平面内的两条相交直线和另一个平面.
1.线面平行的性质定理是由线面平行推出线线平行,此处的线线是指与平面平行的一条直线和过这条直线的平面与已知平面的交线.因此,在应用该定理时,要防止出现“一条直线平行于一个平面就平行于这个平面内的一切直线”这种错误.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com