
题目列表(包括答案和解析)
1.已知集合A={x| x=cos , k∈Z},B={x| x=sin
, k∈Z},B={x| x=sin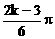 , k∈Z},则有
, k∈Z},则有
(A)A B (B)A
B (B)A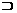 B (C)A≠B (D)A=B
B (C)A≠B (D)A=B
点到直线的距离公式是解析几何常用的基本公式之一.解析几何中的轨迹问题、最值问题、曲线与直线的位置关系等都与点到直线的距离有关,应用点到直线的距离公式能够解决许多重要问题.随着对解析几何的深入学习,我们对点到直线的距离公式及其应用会有更深更广的认识.
4. 求最值(创新应用型)
例5 已知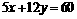 ,求
,求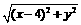 的最小值.
的最小值.
解: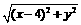 的最小值是点
的最小值是点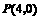 到直线
到直线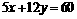 的距离
的距离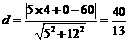 ,
,
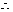 所求最小值为
所求最小值为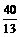 .
.
3. 求方程
利用点到直线的距离可确定直线方程中的参数,从而求得直线方程;利用点到直线的距离列方程可求动点的转迹方程.
例3 已知正方形的中心为直线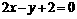 和
和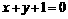 的交点,正方形一边所在的直线为
的交点,正方形一边所在的直线为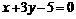 ,求其他三边所在直线的方程.
,求其他三边所在直线的方程.
解:由方程组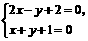 的解,
的解,
可得正方形的中心为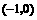 .
.
设正方形相邻两边的方程为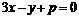 和
和 .
.
因为中心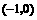 到四边距离相等,故有
到四边距离相等,故有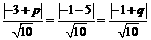 .
.
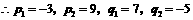 (舍去).
(舍去).
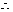 其他三边所在直线的方程分别为
其他三边所在直线的方程分别为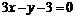 ,
,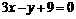 ,
,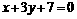 .
.
例4 点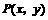 到定点
到定点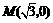 的距离与到直线
的距离与到直线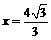 的距离之比为
的距离之比为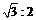 ,求点
,求点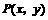 的轨迹方程.
的轨迹方程.
解:由题意,得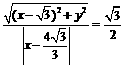 .
.
化简,得所求的轨迹方程为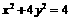 .
.
2. 求点的坐标
例2 求直线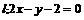 上到直线
上到直线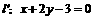 的距离为
的距离为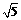 的点的坐标.
的点的坐标.
解:设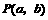 为直线
为直线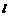 上到
上到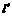 的距离为
的距离为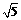 的点,
的点,
则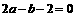 ,
,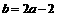 ,所以点
,所以点 的坐标为
的坐标为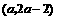 .
.
由点到直线的距离公式,得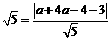 ,
, 或
或 .
.
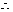 所求点的坐标为
所求点的坐标为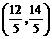 或
或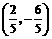 .
.
1. 求距离
例1 已知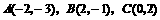 ,求
,求 的面积.
的面积.
分析:欲求 的面积,可先求出直线
的面积,可先求出直线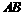 的方程,再求点
的方程,再求点 到直线
到直线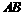 的距离.
的距离.
解:由两点式,可求出直线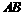 的方程为:
的方程为: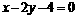 ,点
,点 到直线
到直线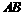 的距离等于
的距离等于 中
中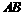 边上的高
边上的高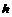 ,
,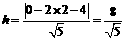 ,又
,又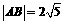 ,
,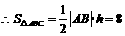 .
.
要牢记上述公式的特点及应用条件,重点掌握公式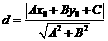 及其应用;还要会利用所得到的方程求点的坐标或求直线方程中的参数、求轨迹方程;有些问题根据图形的几何性质,抓住点到直线的距离这一突破口,就能找到解题捷径.平行线间的距离可转化为点到直线的距离,也可利用平行线间的距离公式求解.
及其应用;还要会利用所得到的方程求点的坐标或求直线方程中的参数、求轨迹方程;有些问题根据图形的几何性质,抓住点到直线的距离这一突破口,就能找到解题捷径.平行线间的距离可转化为点到直线的距离,也可利用平行线间的距离公式求解.
4. 利用点到直线的距离公式,可求得两平行线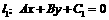 与
与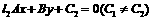 间的距离
间的距离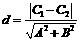 .
.
推导方法如下:由于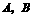 不同时为零,不妨设
不同时为零,不妨设 ,令
,令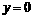 ,得直线
,得直线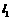 与
与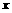 轴的交点
轴的交点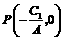 ,点
,点 到直线
到直线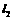 的距离
的距离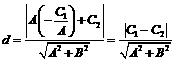 即为两平行线间的距离;当
即为两平行线间的距离;当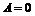 时,公式
时,公式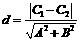 也成立.
也成立.
3. 点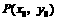 到直线
到直线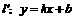 的距离
的距离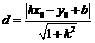 ;
;
2. 点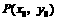 到直线
到直线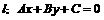 的距离
的距离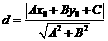 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com