
题目列表(包括答案和解析)
3. 等差数列所有项的和为210,其中前4项的和为40,后4项的和为80,则项数为 。
2. 已知等差数列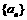 和等比数列
和等比数列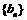 各项都是正数,且
各项都是正数,且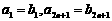 ,那么,一定有
,那么,一定有
A. C.
C.
1. 等差数列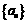 的前n项和为
的前n项和为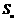 ,若
,若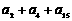 的值为常数,则下列各数中也是常数的是
的值为常数,则下列各数中也是常数的是
A.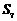 B.
B.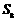 C.
C.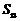 D.
D.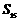
14.设二次函数f(x)=ax2+bx+1(a、b∈R)
(1)若f(-1)=0,且对任意实数x均有f(x)≥0成立,求实数a、b的值;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
解析:(1)f(-1)=0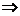 a-b+1=0,即b=a+1.
a-b+1=0,即b=a+1.
又f(x)≥0,对任意实数x均成立,即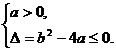
将b=a+1代入有(a-1)2≤0,∴a=1,?b=2.
(2)g(x)=f(x)-kx=x2+(2-k)x+1,对称轴为x=-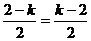 ,
,
因g(x)在[-2,2]上单调,故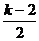 ≤-2或
≤-2或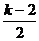 ≥2,
≥2,
∴k的取值范围为k≤-2或k≥6.
13.已知f(x)=x2+ax+b(a,b∈R)的定义域为[-1,1],记|f(x)|的最大值为M.
(1)不等式M≥ 能成立吗?试说明理由;
能成立吗?试说明理由;
(2)当M= 时,求f(x)的解析式.
时,求f(x)的解析式.
解析:(1)由已知得:|f(0)|≤M,|f(1)|≤M,|f(-1)|≤M,
因|2f(0)-f(1)-f(-1)|=2,|2f(0)-f(1)-f(-1)|≤2|f(0)|+|f(1)|+|f(-1)|.
故2≤2M+M+M,即M≥ .
.
(2)当M= 时,|f(0)|≤
时,|f(0)|≤ ,即-
,即- ≤b≤
≤b≤ ①
①
|f(1)|≤ ,即-
,即- ≤1+a+b≤
≤1+a+b≤ .
②
.
②
|f(-1)|≤ ,即-
,即- ≤1-a+b≤
≤1-a+b≤ . ③
. ③
②+③得,-1≤2+2b≤1,所以-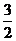 ≤b≤-
≤b≤- .
④
.
④
由①④得b=- ,代入②得-1≤a≤0.
,代入②得-1≤a≤0.
将b=- 代入③得-1≤-a≤0,即0≤a≤1,所以a=0.所以当M=
代入③得-1≤-a≤0,即0≤a≤1,所以a=0.所以当M= 时,f(x)=x2-
时,f(x)=x2- .
.
12.求函数f(x)=4x2-4ax+a2-2a+2在[0,2]上的最值.
解析:f(x)=4(x-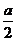 )2-2a+2.
)2-2a+2.
(1)当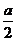 ≤0时,即a≤0,f(x)在[0,2]上递增.
≤0时,即a≤0,f(x)在[0,2]上递增.
∴f(x)max=f(2)=a2-10a+18.
f(x)min=f(0)=a2-2a+2.
(2)当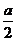 ≥2时,即a≥4时,f(x)在[0,2]上递减.
≥2时,即a≥4时,f(x)在[0,2]上递减.
∴f(x)max=f(0)=a2-2a+2.
f(x)min=f(2)=a2-10a+18.
(3)当0≤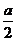 ≤2时,即0≤a≤4时,
≤2时,即0≤a≤4时,
f(x)min=f(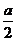 )=-2a+2.
)=-2a+2.
①当0≤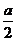 ≤1时,即0≤a≤2时,
≤1时,即0≤a≤2时,
f(x)max=f(2)=a2-10a+18;
②当1≤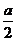 ≤2时,即2≤a≤4时,
≤2时,即2≤a≤4时,
f(x)max=a2-2a+2.
11.已知二次函数的对称轴为x=-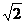 ,截x轴上的弦长为4,且过点(0,-1),求二次函数的解析式.
,截x轴上的弦长为4,且过点(0,-1),求二次函数的解析式.
解法一:设二次函数解析式为y=ax2+bx+c,
依题意有x=-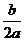 =-
=-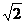 .
①
.
①
图象过点(0,-1),则有c=-1. ②
又截轴的弦长为4,设ax2+bx+c=0的两根为x1、x2,由韦达定理有
|x1-x2|=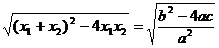 =4.
③
=4.
③
由①②③式联立解得a= ,b=
,b=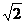 ,c=-1.
,c=-1.
∴二次函数解析式为
y= x2+
x2+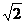 x-1.
x-1.
解法二:设y=a(x+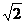 )2+m,由条件得
)2+m,由条件得
-1=2a+m. ①
弦长为4,令y=0,(x+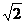 )2=-
)2=-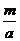 ,
,
则有x=-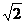 ±
±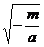 .
.
由|x1-x2|=4,
∴2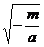 =4.
②
=4.
②
联立①②式解得a= ,m=-2.
,m=-2.
∴二次函数解析式为
y= (x+
(x+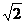 )2-2.
)2-2.
解法三:∵对称轴为x=-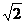 ,又截x轴的弦长为4,则图象与x轴的交点为x1=-2-
,又截x轴的弦长为4,则图象与x轴的交点为x1=-2-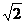 ,x2=2-
,x2=2-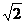 .
.
设二次函数为y=a(x+2+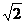 )(x-2+
)(x-2+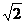 ),
),
又(0,-1)在图象上,则有-1=a(2+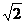 )(-2+
)(-2+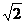 ).
).
∴a= ,二次函数解析式为y=
,二次函数解析式为y= x2+
x2+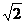 x-1.
x-1.
10.(2010浙江杭州二中模拟,9)设函数f(x)=x|x|+bx+c给出下列四个命题,其中正确的命题是.
①c=0时,y=f(x)是奇函数;②b=0,c>0时,方程f(x)=0只有一个?实根;③y=f(x)的图象关于(0,c)对称;④方程f(x)=0至多有两个实根.
答案:①②③
解析:当c=0时,f(-x)=-x|x|-bx=-f(x),故①正确;y=x|x|+b|x|图象关于原点对称,向上平移c个单位(若c<0,则向下平移|c|个单位),得到f(x)=x·|x|+bx+c,故关于点(0,c)对称;当b=0,c>0时,f(x)=x|x|+c=0不可能有非负根,故x<0,∴x=-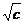 ;令b=-1,c=0,则f(x)=0
;令b=-1,c=0,则f(x)=0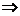 x=0,±1即④为假.
x=0,±1即④为假.
9.已知二次函数y=ax2+bx+c(a>0)的图象与两坐标轴的交点分别为(-1,0)和(0,-1),且顶点在y轴的右侧,则b的取值范围是_________________.
答案:-1<b<0
解析:依题意得,f(-1)=a-b+c=0,f(0)=c=-1,-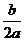 >0,∴b=a-1且b<0.
>0,∴b=a-1且b<0.
又∵a>0,∴-1<b<0.
8.二次函数y=ax2+bx+c(a≠0)的图象如下图,试确定下列各式的正负;b__________,ac__________,a-b+c__________.

答案:>0 <0 <0
解析:由题图知: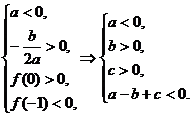
故b<0,ac<0,a-b+c<0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com